一种新非Lipschitz条件下倒向随机微分方程的L²解

L² Solutions of BSDEs with a New Kind of Non-Lipschitz

摘要: 经典的倒向随机微分方程是由布朗运动驱动的，但布朗运动是一种非常特殊的随机过程，致使倒向随机微分方程的应用受到相当大的限制。本文研究了以连续局部鞅为干扰源的一维倒向随机微分方程，在生成元满足一种新非Lipschitz条件下，证明了其L²解存在且唯一。

Abstract: The classical backward stochastic differential equation (BSDE) is driven by the Brownian motion, but Brownian motion is a very special stochastic process, so the application of backward stochastic differential equation is quite limited. In this paper, we are interested in solving one-dimensional backward stochastic differential equations (BSDEs) with a new kind of non-Lipschitz coefficients. We establish an existence and uniqueness result of solutions in L².

1. 引言

倒向随机微分方程在金融数学、最优控制、随机决策和偏微分方程等领域中有着广阔的应用前景。经典的倒向随机微分方程是由布朗运动驱动的，1990年Pardoux和Peng [2] 给出了Lipschitz条件下解的存在唯一性结果。然而Lipschitz条件太强，布朗运动太过于理想化，致使倒向随机微分方程的应用受到相当大的限制。因此，一方面，许多学者开始研究各种非Lipschitz条件下的倒向随机微分方程来改进Pardoux和Peng的关于解的存在唯一性，例如，Fan [1] ，Mao [3] ，Lepeltier和Martin [4] ，Kobylanski [5] 分别给出了非Lipschitz条件下解的存在唯一结果。另一方面，有相当多的学者研究了其他干扰源驱动的倒向随机微分方程，其中，李娟 [6] 研究了连续局部鞅驱动的Lipschitz条件下的倒向随机微分方程，王湘君 [7] 研究过由连续半鞅驱动的Lipschitz条件下的倒向随机微分方程。本文中，我们研究了由连续局部鞅驱动的倒向随机微分方程在Fan [1] 中非Lipschitz条件下解的存在唯一性。

2. 主要结果

令 $\left(\Omega ,,F,，{\{F_t\}}_{t\ge 0},P\right)$ 为一个带信息流的完备的概率空间，其中流 ${\{F_t\}}_{t\ge 0}$ 满足通常条件，记 $\mathcal{P}$ 为可料 σ 域。 $M=\left\{M_t,F_t:0\le t<\infty \right\}$ 为一个连续局部鞅，并且 $M_0=0$， $\langle M\rangle$ 为M的平方变差过程。 $T>0$ 为一个任意固定的数，称为时间区间。

首先给出几个相关记号：

1) 用 $L_M\left(0,T;R^n\right)$ 表示所有使得 ${\Vert x\Vert }_M^2=E{\displaystyle {\int }_0^T{\left|y\left(s\right)\right|}^2}d{\langle M\rangle }_s<+\infty$ 的 $F_t$ -适应的 $R^n$ 值的过程 $x=x\left(s\right)$ 的集合。当 $n=1$ 时简记为 $L_M$。

2) 用 ${L^{\prime }}_M\left(0,T;R^{n\times d}\right)$ 表示所有使得 ${\Vert y\Vert }_M^2=E{\displaystyle {\int }_0^T{\left|z\left(s\right)\right|}^2}d{\langle M\rangle }_s<+\infty$ 的 $F_t$ 可料的 $R^{n\times d}$ 值的过程 $y=y\left(s\right)$ 的集合。当 $n=d=1$ 时简记为 ${L^{\prime }}_M$。

3) 用 $L^2\left(\Omega ,F_T,P;R^n\right)$ 表示所有满足的 $F_T$ -可测的 $R^n$ 值的随机变量 $\xi$ 的集合。当 $n=1$ 时简记为 $L^2\left(\Omega ,F_T,P\right)$。

以下，我们将讨论如下形式的一维倒向随机微分方程：

(1)

其中， $y\left(s\right)$ 为 $F_t$ 适应的过程， $z\left(s\right)$ 为 $F_t$ 可料的过程， $\xi \in L^2\left(\Omega ,F_T,P\right)$， $\left\{M_t,F_t;0\le t<+\infty \right\}$ 为具有零初值的连续局部鞅，具有可料表示性，且 ${\langle M\rangle }_T$ 为有界的，即存在正常数 $C_1$，使得 ${\langle M\rangle }_T\le C_1$ ,a.s.，函数 $g:\Omega \times \left[0,T\right]\times R\times R\to R$ 为 $\mathcal{P}\otimes {\rm B}\left(R\right)\otimes {\rm B}\left(R\right)$ 可测的。

假设方程(1)满足以下条件：

(H1) $g\left(\cdot ,0,0\right)\in L_M$；

(H2) 存在一个单调不减凹函数 $\rho (\cdot ):R^{+}\to R^{+}$，使得 $\forall y_1,y_2\in R,z\in R$ , $\text{d}P\times \text{d}t-a.e.$，

${\left|g\left(w,t,y_1,z\right)-g\left(w,t,y_2,z\right)\right|}^2\le \rho \left({\left|y_1-y_2\right|}^2\right)$

其中 $\rho \left(0\right)=0$， $\forall u>0$， ${\displaystyle {\int }_{0+}\frac{\text{d}u}{\rho \left(u\right)}}=+\infty$。

(H3)存在一个常数 $C\ge 0$，使得 $\forall y\in R,z_1,z_2\in R$ , $\text{d}P\times \text{d}t-a.e.$，

${\left|g\left(w,t,y,z_1\right)-g\left(w,t,y,z_2\right)\right|}^2\le C\left({\left|z_1-z_2\right|}^2\right)$

(H4) $E\left[{\left({\displaystyle {\int }_0^T\left|g\left(t,0,0\right)\right|\text{d}{\langle M\rangle }_t}\right)}^2\right]<+\infty$；

注1: $\rho (\cdot )$ 是一个单调不减凹函数，且 $\rho \left(0\right)=0$，即 $\rho (\cdot )$ 几乎处处是线性增长的，存在一个常数 $A>0$，使得对 $\forall x\ge 0$，有 $\rho \left(x\right)\le A\left(x+1\right)$。

定理1 设函数g满足(H1)—(H4)， $\xi \in L^2\left(\Omega ,F_T,P\right)$，则倒向随机微分方程(1)在 $L^2$ 中有唯一的解。

3. 引理

为了证明定理1，我们还需要用到下面的引理。我们首先来构造倒向随机微分方程(1)的Picard逼近序列，由如下的倒向随机微分方程所定义：

$y_t^0=0;y_t^n=\xi +{\displaystyle {\int }_t^T\left[g\left(s,y_s^{n-1},z_s^n\right)\right]\text{d}{\langle M\rangle }_s}-{\displaystyle {\int }_t^T{z}_s^n\text{d}{M}_s},0\le t\le T$， (2)

其中，生成元 $g\left(s,y_s^{n-1},z_s^n\right)$ 满足(H3)和(H4)，由文献 [8] 定理4.2得，对 $n\ge 1$，方程(2)在 $L^2$ 中有唯一的解 ${\left(y_t^n,z_t^n\right)}_{t\in \left[0,T\right]}$。

由注1和(H2)，容易得

$\left|g\left(s,y_s^{n-1},0\right)\right|\le \left|g\left(s,0,0\right)\right|+{\rho }^{\frac{1}{2}}\left({\left|y_s^{n-1}\right|}^2\right)\le \left|g\left(s,0,0\right)\right|+A^{\frac{1}{2}}\left(\left|y_s^{n-1}\right|+1\right)$

和

$E\left[{\left({\displaystyle {\int }_0^T\left|g\left(s,y_s^{n-1},0\right)\right|}d{\langle M\rangle }_s\right)}^2\right]\le 4E\left[{\left({\displaystyle {\int }_0^T\left|g\left(s,0,0\right)\right|}d{\langle M\rangle }_s\right)}^2\right]+A{\left(2T\right)}^2\left(E\left[\underset{s\in \left[0,T\right]}{\sup }{\left|y_s^{n-1}\right|}^2\right]+1\right)$

引理1 在定理1的假设下，存在一个常数 $c_1>0$ 和常数 $K>0$，且 $c_1$ 只依赖于C，K只依赖于C和T，

使得对任意的 $t\in \left[0,T\right]$， n,m ≥ 1 ，有

$E\left[\underset{s\in \left[t,T\right]}{\sup }{\left|y_s^{n+m}-y_s^n\right|}^2\right]\le \frac{1}{2}{\text{e}}^{c_1\left(T-t\right)}{\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^{n+m-1}-y_s^{n-1}\right|}^2\right]\right)\text{d}{\langle M\rangle }_s}$ (3)

和

$E\left[\underset{s\in \left[t,T\right]}{\sup }\left|z_s^{n+m}-z_s^n\right|\right]\le K\left\{E\left[\underset{s\in \left[t,T\right]}{\sup }{\left|y_s^{n+m}-y_s^n\right|}^2\right]+{\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^{n+m-1}-y_s^{n-1}\right|}^2\right]\right)d{\langle M\rangle }_s}\right\}$ (4)

证明：由方程(2)，得 ${\left(y_t^{n+m}-y_t^n,z_t^{n+m}-z_t^n\right)}_{t\in \left[0,T\right]}$ 是如下方程(5)在 $L^2$ 中的解

$y_t={\displaystyle {\int }_t^T\left[f_{n,m}\left(s,z_s\right)\right]}d{\langle M\rangle }_s-{\displaystyle {\int }_t^T{z}_s\text{d}{M}_s},0\le t\le T$ (5)

其中 $f_{n,m}\left(s,z_s\right)=g\left(s,y_s^{n+m-1},z+z_s^n\right)-g\left(s,y_s^{n-1},z_s^n\right)$。

由(H2)和(H3)，得

$\left|f_{n,m}\left(s,z_s\right)\right|\le {\rho }^{\frac{1}{2}}\left({\left|y_s^{n+m-1}-y_s^{n-1}\right|}^2\right)+C\left|z\right|$ (6)

(6)式意味着方程(5)的生成元 $f_{n,m}\left(s,z_s\right)$ 满足文献 [1] 命题1中的假设(A)，即 $\psi (\cdot )\equiv 0$， $\lambda =C$， $f_t\equiv 0$， ${\phi }_t={\rho }^{\frac{1}{2}}\left({\left|y_s^{n+m-1}-y_s^{n-1}\right|}^2\right)$。又因为 $\rho (\cdot )$ 是一个凹函数，所以由文献 [1] 命题1和命题2，应用Fubini定理和

Jensen不等式，即可得(3)式和(4)式。 证毕。

引理2 在定理1的假设下，存在一个不依赖于 $\xi$ 的 $T_1\in \left[0,T\right]$，常数 $M\ge 0$，使得对 $\forall t\in \left[T_1,T\right],n\ge 1$，有 $E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^n\right|}^2\right]\le N$。

证明：由定理1的假设，得

$\left|g\left(s,y_s^{n-1},z\right)\right|\le \left|g\left(s,y_s^{n-1},z\right)-g\left(s,0,0\right)\right|+\left|g\left(s,0,0\right)\right|\le {\rho }^{\frac{1}{2}}\left({\left|y_s^{n-1}\right|}^2\right)+C\left|z\right|+\left|g\left(s,0,0\right)\right|$

即方程(2)的生成元 $g\left(s,y_s^{n-1},z_s^n\right)$ 满足文献 [1] 命题1中的假设(A)。

又因为 $\rho (\cdot )$ 是一个凹函数，所以由文献 [1] 命题2，应用Fubini定理和Jensen不等式，存在两个只依

赖于C的正常数 $c_2$ 和 $c_3$，使得对 $\forall t\in \left[0,T\right],n\ge 1$，有

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^n\right|}^2\right]\le {\mu }_t+\frac{1}{2}{\text{e}}^{c_3\left(T-t\right)}{\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^{n-1}\right|}^2\right]\right)d{\langle M\rangle }_s}$ (7)

其中 ${\mu }_t=c_2{\text{e}}^{c_3\left(T-t\right)}\left\{E{\left|\xi \right|}^2+E\left[{\left({\displaystyle {\int }_t^T\left|g\left(s,0,0\right)\right|\text{d}{\langle M\rangle }_s}\right)}^2\right]\right\}\ge 0$

令 $N=2{\mu }_0+2AT$， $T_1=\max \left\{T-\frac{\ln 2}{c_1},T-\frac{\ln 2}{c_3},T-\frac{1}{2}A,0\right\}$，其中 $c_1$ 是引理1中的，A是注1中的,则对，有

$\frac{1}{2}{\text{e}}^{c_1\left(T-t\right)}\le 1,\frac{1}{2}{\text{e}}^{c_3\left(T-t\right)},A\left(T-t\right)\le \frac{1}{2}$ (8)

由(7)和(8)，得

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^n\right|}^2\right]\le {\mu }_0+\frac{1}{2}{\text{e}}^{c_3\left(T-t\right)}{\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^{n-1}\right|}^2\right]\right)d{\langle M\rangle }_s},t\in \left[T_1,T\right]$ (9)

又因为 $\rho (\cdot )$ 是一个单调不减函数，由(9)式，注1和(8)式，得 $\forall t\in \left[T_1,T\right]$，

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^n\right|}^2\right]\le N$，证毕。

4. 定理1的证明

先证存在性。先定义一个函数列 ${\left\{{\phi }_n\left(t\right)\right\}}_{n\ge 1}$ 如下：

${\phi }_0\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}\rho \left(N\right)\text{d}{\langle M\rangle }_s};{\phi }_{n+1}(t)={\displaystyle \underset{t}{\overset{T}{\int }}\rho \left({\phi }_n\left(s\right)\right)\text{d}{\langle M\rangle }_s}$ (10)

对 $\forall t\in \left[T_1,T\right]$，由引理2，得

${\phi }_0\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}\rho \left(N\right)\text{d}{\langle M\rangle }_s}\le M$，

${\phi }_1\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}\rho \left({\phi }_0\left(s\right)\right)d{\langle M\rangle }_s}\le {\displaystyle \underset{t}{\overset{T}{\int }}\rho \left(N\right)d{\langle M\rangle }_s}={\phi }_0\left(t\right)\le M$，

${\phi }_2\left(t\right)={\displaystyle \underset{t}{\overset{T}{\int }}\rho \left({\phi }_1\left(s\right)\right)d{\langle M\rangle }_s}\le {\displaystyle \underset{t}{\overset{T}{\int }}\rho \left({\phi }_0\left(s\right)\right)d{\langle M\rangle }_s}={\phi }_1\left(t\right)\le M$。

由数学归纳法，可得

$0\le {\phi }_{n+1}\left(t\right)\le {\phi }_n\left(t\right)\le \cdots \le {\phi }_1\left(t\right)\le {\phi }_0\left(t\right)\le M$。

因此，对 $\forall t\in \left[T_1,T\right]$，函数列 ${\left\{{\phi }_n\left(t\right)\right\}}_{n\ge 1}$ 极限存在，记为 $\phi \left(t\right)$。

因为 $\rho (\cdot )$ 是一个连续函数，且 $\rho \left({\phi }_n\left(s\right)\right)\le \rho \left(N\right)$，令 $n\to \infty$，对(10)式取极限，由Lebesgue收敛定理，对 $\forall t\in \left[T_1,T\right]$，有

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^n\right|}^2\right]\le N$，

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^{1+m}-y_r^1\right|}^2\right]\le {\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^m\right|}^2\right]\right)d{\langle M\rangle }_s}\le {\displaystyle \underset{t}{\overset{T}{\int }}\rho \left(N\right)d{\langle M\rangle }_s}={\phi }_0\left(t\right)\le M$，

$E\left[\underset{r\in \left[t,T\right]}{\sup }{\left|y_r^{2+m}-y_r^2\right|}^2\right]\le {\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_r^{\text{1+}m}-y_r^1\right|}^2\right]\right)d{\langle M\rangle }_s}\le {\displaystyle \underset{t}{\overset{T}{\int }}\rho \left({\phi }_0\left(s\right)\right)d{\langle M\rangle }_s}={\phi }_1\left(t\right)\le M$。

由数学归纳法，可得

$E\left[\underset{r\in \left[T_1,T\right]}{\sup }{\left|y_r^{\text{n+}m}-y_r^n\right|}^2\right]\le {\phi }_{n-1}\left(T_1\right)\to 0,n\to \infty$

即 ${\left\{y_t^n\right\}}_{n\ge 1}$ 是cauchy序列,又因为 $\rho (\cdot )$ 是一个连续函数，由引理1中的(4)式知， ${\left\{z_t^n\right\}}_{n\ge 1}$ 也是cauchy序列，它们的极限分别记为 ${\left\{y_t\right\}}_{t\in \left[T_1,T\right]}$ 和 ${\left\{y_t\right\}}_{t\in \left[T_1,T\right]}$。令 $n\to \infty$，对(2)式取极限，可得 $\left\{y_t,z_t\right\}$ 是具有参数 $\left(\xi ,T,g\right)$ 的BSDE在 $\left[T_1,T\right]$ 的 $L^2$ 解。

可以通过迭代可得， $\forall l$，方程(1)在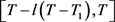有解，因此可得，方程(1)在 $\left[0,T\right]$ 上解的存在性。

再证唯一性：设 ${\left\{y_t^1,z_t^1\right\}}_{t\in \left[0,T\right]}$ 和 ${\left\{y_t^2,z_t^2\right\}}_{t\in \left[0,T\right]}$ 都是方程(1)的 $L^2$ 解，则

是如下方程(11)的 $L^2$ 解。

$y_t={\displaystyle {\int }_t^T\left[\hat{g}\left(s,y_s,z_s\right)\right]}d{\langle M\rangle }_s-{\displaystyle {\int }_t^T{z}_s\text{d}{M}_s},0\le t\le T$ (11)

其中， $\hat{g}\left(s,y_s,z_s\right)=g\left(s,y+y_s^2,z+z_s^2\right)-\hat{g}\left(s,y_s^2,z_s^2\right)$。

由(H2)和(H3)，可得 $\left|\hat{g}\left(s,y_s,z_s\right)\right|\le {\rho }^{\frac{1}{2}}\left({\left|y\right|}^2\right)+C\left|z\right|$，即方程(11)的生成元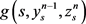满足文献 [1] 命题

1中的假设(A)。

由文献 [1] 命题1和命题2，存在一个只依赖于C的正常数 $c_4$ 和一个只依赖于C和T的正常数 $c_5$，使

得对 $\forall t\in \left[0,T\right]$，有

$E\left[{\left|y_t^1-y_t^2\right|}^2\right]\le \frac{1}{2}{\text{e}}^{c_4\left(T-t\right)}{\displaystyle {\int }_t^T\rho \left(E\left[{\left|y_s^1-y_s^2\right|}^2\right]\right)d{\langle M\rangle }_s}$ (12)

和

$E\left[\left({\displaystyle {\int }_t^T{\left|z_s^1-z_s^2\right|}^2\text{d}{\langle M\rangle }_s}\right)\right]\le c_5\left\{E\left[\underset{s\in \left[t,T\right]}{\sup }{\left|y_s^1-y_s^2\right|}^2\right]+\rho \left(E\left[\underset{s\in \left[t,T\right]}{\sup }{\left|y_s^1-y_s^2\right|}^2\right]\right)\right\}$。 (13)

对(12)式应用Bihari’s不等式，得 $E\left[{\left|y_t^1-y_t^2\right|}^2\right]=0,t\in \left[0,T\right]$，因此 $y_t^1=y_t^2,t\in \left[0,T\right],a.s.$，再由(13)式,又可得 $z_t^1=z_t^2,t\in \left[0,T\right],a.s.$，唯一性得证。

基金项目

国家自然科学基金资助项目(11561028，11801238)，江西省教育厅青年科学基金资助项目(GJJ170566，GJJ170567，GJJ170525)，江西理工大学大学生创新创业训练项目(DC2018-072)，江西理工大学本科教学工程项目(XZG-16-01-05)。