一种基于贝叶斯判别的信用评分方法

A Credit Scoring Technology Based on Bayes Discriminant Analysis

摘要: 本文借鉴了FICO评分的思想，基于贝叶斯判别定理推导出一套评分模型，评分模型最终为一个目标函数是线性函数，约束条件含有二次等式约束的最优化问题。最后，通过一个实例与Logistic回归做了对比，实例结果表明模型是有效的，且模型能够更好的支持实际业务应用场景。

Abstract: According to FICO Score theory and Bayes Discrimination, the credit scoring model is derived, which ends up as an optimization model with linear objective function and quadratic equality constraints. Finally, compared with Logistic Regression through an example, the result shows that the credit scoring model is effective and can support application scenarios of practical business better.

1. 概述

在信用评分方面，美国Fair Isaac Corp公司的评分(以下简称FICO评分 [1] )是应用最为成熟的一种评分模型，该评分在300~850之间，信用评分越高，说明客户的信用风险越小。除此之外，Logistic回归 [2] [3] 、决策树、神经网络等也是常用的评分方法。

本文借鉴了FICO评分的思想，并基于贝叶斯判别定理推导出了一套信用评分模型(以下简称评分模型)，该模型是一个目标函数为线性函数，约束条件为二次型的最优化模型。本文评分模型所具有的优点是：

① 本文评分模型得到的是非常直观的整数权重，这对不懂评分技术的业务人员来讲，能够很方便的对评分结果进行解读和应用。

② 当业务人员拒绝客户的信用业务申请时，可以依据评分结果给予合理的拒绝原因。

③ 利用本文评分模型得到的多张评分卡，可以方便的比较、混合使用。

④ 鉴于以往的项目经验：本文评分模型的稳健性是非常好的，利用本文方法建立好的评分卡应用3年后仍然有很好的预测性，而Logistic回归、决策树要逊色很多。

2. 基于贝叶斯判别的评分模型

评分模型的建立分为5个步骤：输入变量的筛选、输入变量的分箱、评分模型的求解与评估、评分结果的拟合与尺度化、评分模型的部署。

本文研究的内容主要是：评分模型的建立、评分结果的拟合与尺度化。

假设有一批信用良好的客户样本(以下简称好客户样本)和信用不良的客户样本(以下简称坏客户样本)，我们要通过这两组样本数据建立评分模型。基于以往业务经验对评分模型做如下要求和假设：

① 客户信用评分S越大，代表该客户是好客户的概率越大；反之，代表是坏客户的概率越大。

② 好客户样本评分 $S_g$ 服从正态分布 $N\left({\bar{S}}_g,{\sigma }_g^2\right)$， ${\bar{S}}_g$ 为好客户样本均值， ${\sigma }_g^2$ 为好客户样本方差； $S_g$ 的密度函数为 $f_g\left(S\right)$。

③ 坏客户样本评分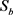服从正态分布 $N\left({\bar{S}}_b,{\sigma }_b^2\right)$， ${\bar{S}}_b$ 为坏客户样本均值， ${\sigma }_b^2$ 为坏客户样本方差； $S_b$ 的密度函数为 $f_b\left(S\right)$。

④ $p\left(g|S\right)$：信用评分为S的客户是好客户的概率； $p\left(b|S\right)$：信用评分为S的客户是坏客户的概率；

⑤ $odds\left(S\right)=p\left(g|S\right)/p\left(b|S\right)$：信用评分S对应的好、坏客户的概率比。

⑥ 评分模型有p个输入变量，各分箱组数分别是 $q_1,q_2,\cdots ,q_p$ 个，各分箱权重分别如下：

第1个输入变量的分箱权重为： $w_{11},\cdots ,w_{1q_1}$

.......

第p个输入变量的分箱权重为： $w_{p1},\cdots ,w_{p{q}_p}$

记： $w={\left(w_{11},\cdots ,w_{1q_1},w{}_{21},\cdots ,w_{2q_2},\cdots ,w_{p{q}_p}\right)}^{\text{T}}$； $T={\displaystyle \underset{i=1}{\overset{p}{\sum }}{q}_i}$：总共分箱组数。

⑦ 好客户样本m个，分别为： $g^{\left(1\right)},\cdots ,g^{\left(m\right)}$；坏客户样本n个，分别为： $b^{\left(1\right)},\cdots ,b^{\left(n\right)}$。

$g^{\left(r\right)}={\left(g_{11}^{\left(r\right)},\cdots ,g_{1q_1}^{\left(r\right)},\cdots ,g_{p1}^{\left(r\right)},\cdots ,g_{p{q}_p}^{\left(r\right)}\right)}^{\text{T}}$ $\left(1\le r\le m\right)$

$b^{\left(r\right)}={\left(b_{11}^{\left(r\right)},\cdots ,b_{1q_1}^{\left(r\right)},\cdots ,b_{p1}^{\left(r\right)},\cdots ,b_{p{q}_p}^{\left(r\right)}\right)}^{\text{T}}$ $\left((1\le r\le n\right)$

注：对于每个样本第 $i\left(1\le i\le p\right)$ 个输入变量的分箱取值 $x_{i,1},x_{i,2},\cdots ,x_{i,q_i}$ 中，有且仅有一个分箱值为1，其他值为0，表示该样本第i输入变量值落在取值为1的分箱区间内。

⑧ 样本中好客户占比 $p_g=m/\left(m+n\right)$，坏客户占比 $p_b=n/\left(m+n\right)$。

⑨ $S_{g^{\left(r\right)}}$：第r个好客户样本的信用评分 $\left(1\le r\le m\right)$； $S_{b^{\left(r\right)}}$：第r个坏客户样本的信用评分 $\left(1\le r\le n\right)$。

基于①、②、③的要求和假设，我们可以画出评分分布示意图如图1所示：

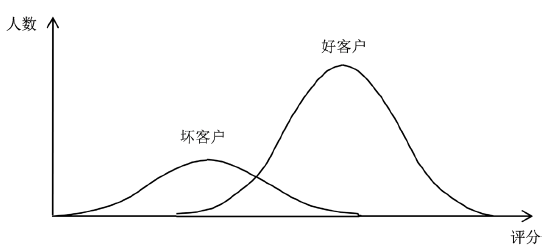
Figure 1. The diagram of score distribution

图1. 评分分布示意图

为了能尽量区分好、坏客户两个群体，显然好客户的信用评分应该尽量大，坏客户的信用评分应该尽量小，我们以此建立我们评分模型的目标函数：

$\max {\displaystyle \underset{r=1}{\overset{m}{\sum }}{S}_{g^{\left(r\right)}}}-{\displaystyle \underset{r=1}{\overset{n}{\sum }}{S}_{b^{\left(r\right)}}}$ (1)

接下来，我们确定评分模型的约束条件：

首先，由贝叶斯判别定理 [4] [5] ，可得

$p\left(g|S\right)=p_g\cdot f_g\left(S\right),p\left(b|S\right)=p_b\cdot f_b(S)$

$\ln \left(odds\left(S\right)\right)=\ln \left(p_g/p_b\right)+\ln \left(f_g\left(S\right)/f_b\left(S\right)\right)$ (2)

为了在拟合阶段中，评分结果与客户好坏的概率值能建立函数关系，我们在模型建立时就要考虑评分S与 $p\left(g|S\right),p\left(b|S\right)$ 的关系。

由于 $\ln \left(p_g/p_b\right)$ 是个定值，不妨就假设： $\ln \left(odds\left(S\right)\right)=\ln \left(p_g/p_b\right)+S$

即 $S=\ln \left(f_g\left(S\right)/f_b\left(S\right)\right)$ (3)

这样就建立了S与 $p\left(g|S\right),p\left(b|S\right)$ 的函数关系，且S越大， $p\left(g|S\right)$ 越大， $p\left(b|S\right)$ 越小。

又因为 $S_g~N\left({\bar{S}}_g,{\sigma }_g^2\right)$， $S_b~N\left({\bar{S}}_b,{\sigma }_b^2\right)$，所以

$\begin{array}{c}\ln \left(f_g\left(S\right)/f_b\left(S\right)\right)=\ln \left(\frac{1}{\sqrt{2\text{π}}{\sigma }_g}\exp \left(-\frac{{\left(S-{\bar{S}}_g\right)}^2}{2{\sigma }_g^2}\right)\right)-\ln \left(\frac{1}{\sqrt{2\text{π}}{\sigma }_b}\exp -\frac{{\left(S-{\bar{S}}_b\right)}^2}{2{\sigma }_b^2}\right)\\ =\left(\frac{1}{2{\sigma }_b^2}-\frac{1}{2{\sigma }_g^2}\right)\cdot S^2+\left(\frac{{\bar{S}}_g}{{\sigma }_g^2}-\frac{{\bar{S}}_b}{{\sigma }_b^2}\right)\cdot S+\left(\frac{{\bar{S}}_b^2}{2{\sigma }_b^2}-\frac{{\bar{S}}_g^2}{2{\sigma }_g^2}\right)\end{array}$

由(3)得 ${\sigma }_g^2={\sigma }_b^2$， ${\bar{S}}_g-{\bar{S}}_b={\sigma }_g^2$， ${\bar{S}}_g+{\bar{S}}_b=0$。

这样我们就可以得到一个初步的评分模型：

$\begin{array}{l}\max {\displaystyle \underset{r=1}{\overset{m}{\sum }}{S}_{g^{\left(r\right)}}}-{\displaystyle \underset{r=1}{\overset{n}{\sum }}{S}_{b^{\left(r\right)}}}\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}{\sigma }_g^2-{\sigma }_b^2=0\\ {\bar{S}}_g-{\bar{S}}_b={\sigma }_g^2\\ {\bar{S}}_g+{\bar{S}}_b=0\end{array}\end{array}$ (4)

实际上，好、坏客户两类群体信用评分的方差一般不会完全相等，而且在数据测试中我们发现 ${\sigma }_g^2$ 、 ${\sigma }_b^2$ 不需要严格相等，效果会更好一些，这样我们可以把约束条件 ${\sigma }_g^2-{\sigma }_b^2=0$ 去掉，同时 ${\bar{S}}_g-{\bar{S}}_b={\sigma }_g^2$ 改为 ${\bar{S}}_g-{\bar{S}}_b=0.5\cdot \left({\sigma }_g^2+{\sigma }_b^2\right)$。

另外，如果对S不加约束，由(4)求得的目标函数会异常大，甚至求不出最优解，因此需要对信用评分S的取值范围加以约束，可以想到的方法有：

① 直接将S约束在某一区间范围内；

② 将每个分箱权重约束在某一范围内；

③ 设定各分箱权重的平方和小于某个阈值。

这3种方法都是有效的，但我们发现：第3种约束效果要好一些。另外，考虑到不同的评分模型其分箱组数是会不一样的，为了模型的普适性，我们采用“各分箱权重平方和的平均值小于某个阈值”来对S进行约束。这样，评分模型进一步优化为：

$\begin{array}{l}\max {\displaystyle \underset{r=1}{\overset{m}{\sum }}{S}_{g^{\left(r\right)}}}-{\displaystyle \underset{r=1}{\overset{n}{\sum }}{S}_{b^{\left(r\right)}}}\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}{\bar{S}}_g-{\bar{S}}_b=0.5\cdot \left({\sigma }_g^2+{\sigma }_b^2\right)\\ {\bar{S}}_g+{\bar{S}}_b=0\\ \frac{1}{T}\cdot {\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q_i}{\sum }}{w}_{ij}^2}}\le K\end{array}\end{array}$ (5)

其中，T为分箱组数，K为阈值(在本文实例计算中， $K=2$ 效果比较理想)。

3. 评分模型的参数推导

下面我们进行具体的参数推导，由前面的假设我们可以得出：

第r个好客户样本的信用评分：

$S_{g^{\left(r\right)}}={\left(g^{\left(r\right)}\right)}^{\text{T}}\cdot w={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q_i}{\sum }}{g}_{ij}^{\left(r\right)}\cdot w_{ij}}}$ $\left(1\le r\le m\right)$

第 $r$ 个坏客户样本的信用评分：

$S_{b^{\left(r\right)}}={\left(b^{\left(r\right)}\right)}^{\text{T}}\cdot w={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q_i}{\sum }}{b}_{ij}^{\left(r\right)}\cdot w_{ij}}}$ $\left(1\le r\le n\right)$

好客户样本信用评分之和：

${\displaystyle \underset{r=1}{\overset{m}{\sum }}{S}_{g^{\left(r\right)}}}={\displaystyle \underset{r=1}{\overset{m}{\sum }}{\left(g^{\left(r\right)}\right)}^{\text{T}}\cdot w}=\left({\displaystyle \underset{r=1}{\overset{m}{\sum }}{\left(g^{\left(r\right)}\right)}^{\text{T}}}\right)\cdot w$

坏客户样本信用评分之和：

${\displaystyle \underset{r=1}{\overset{n}{\sum }}{S}_{b^{\left(r\right)}}}={\displaystyle \underset{r=1}{\overset{n}{\sum }}{\left(b^{\left(r\right)}\right)}^{\text{T}}\cdot w}=\left({\displaystyle \underset{r=1}{\overset{n}{\sum }}{\left(b^{\left(r\right)}\right)}^{\text{T}}}\right)\cdot w$

好客户样本信用评分平均值：

${\bar{S}}_g=\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{S}_{g^{\left(r\right)}}}=\left(\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{\left(g^{\left(r\right)}\right)}^{\text{T}}}\right)\cdot w$

坏客户样本信用评分平均值：

${\bar{S}}_b=\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{S}_{b^{\left(r\right)}}}=\left(\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{\left(b^{\left(r\right)}\right)}^{\text{T}}}\right)\cdot w$

好客户样本信用评分方差：

$\begin{array}{c}{\sigma }_g^2=E{\left(S_g-{\bar{S}}_g\right)}^2=\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{\left(S_g^{\left(r\right)}-{\bar{S}}_g\right)}^2}=\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{\left({\left(g^{\left(r\right)}-\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}}\right)}^{\text{T}}\cdot w\right)}^2}\\ =\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}\left(w^{\text{T}}\cdot \left(g^{\left(r\right)}-\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}}\right)\cdot {\left(g^{\left(r\right)}-\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}}\right)}^{\text{T}}\cdot w\right)}\\ =\frac{1}{m}{w}^{\text{T}}\cdot {\displaystyle \underset{r=1}{\overset{m}{\sum }}\left(\left(g^{\left(r\right)}-\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}}\right)\cdot {\left(g^{\left(r\right)}-\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}}\right)}^{\text{T}}\right)}\cdot w\end{array}$

同理，坏客户样本信用评分方差：

${\sigma }_b^2=E{\left(S_b-{\bar{S}}_b\right)}^2=\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{\left(S_b^{\left(r\right)}-{\bar{S}}_b\right)}^2}=\frac{1}{n}{w}^{\text{T}}\cdot {\displaystyle \underset{r=1}{\overset{n}{\sum }}\left(\left(b^{\left(r\right)}-\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{b}^{\left(r\right)}}\right){\left(b^{\left(r\right)}-\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{b}^{\left(r\right)}}\right)}^{\text{T}}\right)}\cdot w$

令 $\begin{array}{l}g={\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}},\bar{g}=\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}{g}^{\left(r\right)}},H_g=\frac{1}{m}{\displaystyle \underset{r=1}{\overset{m}{\sum }}\left(g^{\left(r\right)}-\bar{g}\right){\left(g^{\left(r\right)}-\bar{g}\right)}^{\text{T}}},\\ b={\displaystyle \underset{r=1}{\overset{m}{\sum }}{b}^{\left(r\right)}},\bar{b}=\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}{b}^{\left(r\right)}},H_b=\frac{1}{n}{\displaystyle \underset{r=1}{\overset{n}{\sum }}\left(b^{\left(r\right)}-\bar{b}\right){\left(b^{\left(r\right)}-\bar{b}\right)}^{\text{T}}}\end{array}$

则

最后，我们的评分模型就可以表示为：

$\begin{array}{l}\text{max}\left(g^{\text{T}}-b^{\text{T}}\right)\cdot w\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}\left({\bar{g}}^{\text{T}}-{\bar{b}}^{\text{T}}\right)\cdot w=0.5\cdot w^{\text{T}}\cdot \left(H_g+H_b\right)\cdot w\\ \left({\bar{g}}^{\text{T}}+{\bar{b}}^{\text{T}}\right)\cdot w=0\\ \frac{1}{T}\cdot w^{\text{T}}\cdot w\le K\end{array}\end{array}$ (6)

T为分箱组数，K为阈值， $w$ 是我们要求解的分箱权重向量，模型是一个二次型最优化问题 [6] 。

4. 评分结果的拟合与尺度化

在模型建立中，我们假设：

$\ln \left(odds\left(S\right)\right)=\ln \left(p_g/p_b\right)+S$

因此，我们采取 $S,\ln \left(odds\left(S\right)\right)$ 进行线性拟合。

在信用评分的实际应用中，我们往往对某一具体的好坏概率比 $odds\left(S_0\right)$ 特别重视，期望该 $odds\left(S_0\right)$ 对应某个评分 ${S^{\prime }}_0$，不仅如此，还要求信用评分 $S^{\prime }$ 每增加一个固定值 $\Delta {S^{\prime }}_0$，好坏概率比 $odds\left(S^{\prime }\right)$ 就增加一个 $odds\left(S_0\right)$。例如：我们期望好坏概率比为100时对应的信用评分为500分，且信用评分每增加20分，好坏概率比就增加100，当信用评分为700分时，可以推算出好坏概率比为1100。

在此做如下假设：

$S^{\prime }$：S对应的尺度化后评分。

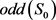：预设的好坏概率比。

$S_0$： $odds\left(S_0\right)$ 对应的尺度化前评分。

${S^{\prime }}_0$： $odds\left(S_0\right)$ 对应的尺度化后评分。

$\Delta {S^{\prime }}_0$：表示尺度化后的评分值每增加 $\Delta {S^{\prime }}_0$，好坏概率比就增加1个 $odds\left(S_0\right)$。

$w^{\prime }={\left({w^{\prime }}_{11},\cdots ,{w^{\prime }}_{1q_1},\cdots ,{w^{\prime }}_{p1},\cdots ,{w^{\prime }}_{p{q}_p}\right)}^{\text{T}}$：尺度化后的各变量分箱权重。

进一步假设 $S,\ln \left(odds\left(S\right)\right)$ 拟合得到的线性方程为：

$\ln \left(odds\left(S\right)\right)=b_0+b_1\cdot S$ ( $b_0,b_1$ 是系数) (7)

则我们可以得出如下关系：

$\ln \left(odds\left(S^{\prime }\right)\right)=\ln \left(odds\left(S\right)\right)=b_0+b_1\cdot S$ (8)

$\frac{\ln \left(odds\left(S^{\prime }\right)\right)-\ln \left(odds\left({S^{\prime }}_0\right)\right)}{S^{\prime }-{S^{\prime }}_0}=\frac{\ln \left(2\cdot odds\left({S^{\prime }}_0\right)\right)-\ln \left(odds\left({S^{\prime }}_0\right)\right)}{\Delta {S^{\prime }}_0}$

即 $\ln \left(odds\left(S^{\prime }\right)\right)=\frac{\ln 2}{\Delta {S^{\prime }}_0}\cdot S^{\prime }+\ln \left(odds\left({S^{\prime }}_0\right)\right)-\frac{\ln 2}{\Delta {S^{\prime }}_0}\cdot {S^{\prime }}_0$ (9)

由(8)进一步可得：

$\ln \left(odds\left({S^{\prime }}_0\right)\right)=\ln \left(odds\left(S_0\right)\right)=b_0+b_1\cdot S_0$ (10)

将(8)、(10)代入(9)，得：

$\begin{array}{l}{b}_0+b_1\cdot S=\frac{\ln 2}{\Delta {S^{\prime }}_0}\cdot S^{\prime }+b_0+b_1\cdot S_0-\frac{\ln 2}{\Delta {S^{\prime }}_0}\cdot {S^{\prime }}_0\\ S^{\prime }=\Delta {S^{\prime }}_0\cdot \frac{b_1}{\ln 2}\cdot S+{S^{\prime }}_0-\Delta {S^{\prime }}_0\cdot \frac{b_1}{\ln 2}\cdot S_0\end{array}$

令 $c_1=\Delta {S^{\prime }}_0\cdot \frac{b_1}{\ln 2}$， $c_0={S^{\prime }}_0-c_1\cdot S_0$，则

$S^{\prime }=c_0+c_1\cdot S$ (11)

$\ln \left(odds\left(S^{\prime }\right)\right)=b_0-\frac{b_1\cdot c_0}{c_1}+\frac{b_1}{c_1}\cdot S^{\prime }$ (12)

式(11)就是尺度化评分 $S^{\prime }$ 与原始评分S的尺度化关系，式(12)就是尺度化后评分 $S^{\prime }$ 与好坏概率比的关系。

需要补充说明是：利用式(7)进行拟合时，实际上并不知道每个原始评分S对应的好坏客户概率比，但是我们可以对原始评分进行排序分组，然后取每个分组原始评分的中间值作为S，每个组的好坏客户数比作为 $odds\left(S\right)$，这样就可以进行拟合了。另外，考虑到按原始评分排序分组以后，S值最大的几个组里可能没有坏客户，S值最小的几个组里可能没有好客户，所以要剔除这些“特殊”组，然后再进行拟合。

最后，我们将尺度化评分 $S^{\prime }$ 拆分到每个变量分箱中。拆分时要遵循如下2条原则：

① 每个变量的各分箱权重非负。

② 各样本的尺度化分箱权重之和仍为 $S^{\prime }$。

记第i个变量的尺度化前最小分箱权重 $\min \left(w_i\right)=\underset{1\le j\le q_i}{\min }\left(w_{ij}\right)\left(1\le i\le p\right)$，则

${w^{\prime }}_{ij}=c_1\cdot \left(w_{ij}+\left|\min \left(w_i\right)\right|\right)+\frac{c_0-c{}_1\cdot {\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|\min \left(w_i\right)\right|}}{p}\left(1\le i\le p,1\le j\le q_i\right)$ (13)

其中 $w_{ij}+\left|\min \left(w_i\right)\right|$ 是为了将变量的最小分箱权重由负值变为零值，乘以 $c_1$ 表示的是每个分箱权重的尺度化也服从S到 $S^{\prime }$ 的线性关系，加上 $\left(c_0-c_1\cdot {\displaystyle \underset{i=1}{\overset{p}{\sum }}\left|\min \left(w_i\right)\right|}\right)/p$ 是为了保证尺度化后的评分值仍然等于尺度化后的分箱权重之和。

例如：假设 $c_0=115.8,c_1=23,\Delta {S^{\prime }}_0=20$，有3个分箱变量，尺度化过程可用如表1所示：

Table 1. Weight scaling for binning variables

表1. 分箱权重尺度化步骤说明表

5. 数据测试与对比

数据来源：SPSS自带的bankloan.sav数据，包含：517位拖欠贷款客户(坏客户)，183位不拖欠贷款客户(好客户)。

输出变量：default (1：坏客户；0：好客户)。

输入变量及分箱结果：见表2。

尺度化要求：500分对应的好坏概率比是100:1，且尺度化后的评分每增加20分，好坏概率比增加100。

阈值设置：K = 2。

利用样本数据计算结果如表3所示：

Table 2. The binning of input variables

表2. 输入变量及分箱表

Table 3. Calculating results of the scoring model

表3. 评分模型计算结果

尺度化评分 $S^{\prime }$ 与 $\ln \left(odds\left(S^{\prime }\right)\right)$ 如图2所示：

Figure 2. Linear fitting chart by $S^{\prime }$ and $\ln \left(odds\left(S^{\prime }\right)\right)$

图2. $S^{\prime }$ 与 $\ln \left(odds\left(S^{\prime }\right)\right)$ 拟合直线图

本文评分模型与Logistic回归ROC曲线比较，如图3所示：

Figure 3. ROC curve comparison chart

图3. ROC曲线对比图

可以看出：文中的评分模型跟Logistic回归模型相比也是一种非常有效的评分方法。另外，基于以往的项目经验：本文评分模型的稳健性是非常好的，利用本文方法建立的评分卡应用3年后仍然有很好的预测性，而Logistic回归、决策树要逊色很多。