深沪股市的波动率分析——基于GARCH和SV模型

Volatility Analysis of Shenzhen and Shanghai Stock Markets—Based on GARCH and SV Models

摘要: 本文选取2016年1月至2019年5月上证综指和深证综指日股收盘价作为原始数据，计算出两者收益率，分析了两市股票收益率的波动情况，通过建立GARCH模型以及SV模型，结果表明GARCH和SV模型均能较好地阐述和拟合我国股市的收益率的波动，并通过EGARCH检验发现收益率存在杠杆效应。从而对股市波动强度趋于平稳以及降低股市风险提出针对性建议。

Abstract: This paper selects the closing prices of Shanghai Composite Index and Shenzhen Composite Index from January 2016 to May 2019 as the original data, calculates the return rates of the two indexes, and analyzes the fluctuation of the stock return rates in the two cities. Through the establishment of GARCH model and SV model, the results show that GARCH model and SV model can well describe and fit the fluctuation of the return rate in China's stock market, and through EGARCH test, it is found that the return rate has leverage effect. Therefore, some suggestions are put forward to stabilize the fluctuation intensity of the stock market and reduce the risk of the stock market.

1. 前言

2019年5月11日，证监会主席易会满出席中国上市公司协会2019年年会暨第二届理事会第七次会议并发表讲话中提到：近期A股面临着大幅波动的情况，股市有一定的震荡波动。资本市场是实体经济的“晴雨表”，最近一段时间以来中国股市出现了明显的波动和下滑，这是由诸多因素造成的。在我国金融体系中，由于市场形势瞬息万变，牵动着股市市场随之变化和发展。我国股票市场的波动强烈是有目共睹的，因此分析我国股市问题迫在眉睫，将如何采取最合适的手段和方法来进行有效地刻画股票市场的波动以及衡量它们的风险？

之前已有很多学者采用综合股指日股收盘价的收益率数据通过不同的模型来分析波动情况。他们通常通过条件异方差来描述金融市场的金融资产收益的波动情况。Engle (1982) [1] 提出了ARCH模型，紧接着Bollerslev (1986) [2] 建立在ARCH的模型基础上，提出了GARCH模型，同年Taylor [3] 提出了随机波动模型(简称SV)，正是由于金融数据具有尖峰厚尾性这个特征不适用于随机误差项服从正态分布，因此引入残差服从t分布这一假设与模型相结合进行实证分析和研究。

2. GARCH模型

2.1. ARCH模型

通常地，有回归模型 $y_t={x^{\prime }}_t\beta +{\epsilon }_t$ ，将 $$ 视为收益或是收益残差，且服从AR(q)过程，假设 ${\epsilon }_t={\sigma }_t{m}_t$ ，此外 $m_t~iidN\left(0,1\right)$ ，关于 ${\sigma }_t^2$ 建模为：

${\epsilon }_t^2={\alpha }_0+{\alpha }_1{\epsilon }_{t-1}^2+\cdots +{\alpha }_p{\epsilon }_{t-q}^2+{\eta }_t$ (1)

其中 $t=1,2,\cdots ,{\eta }_t$ 独立同分布，并满足 $E\left({\eta }_t\right)=0$ ， $D\left({\eta }_t\right)={\lambda }^2$ ，那么该模型被称为ARCH模型(自回归条件异方差模型)。简记ARCH模型。称序列 ${\epsilon }_t^2$ 服从q阶的ARCH过程，记作 ${\epsilon }_t~\text{ARCH}\left(q\right)$ [4] 。

2.2. GARCH模型

GARCH与ARCH模型较为相似，是建立在ARCH模型的基础上，一种广义的表达，GARCH模型通常用于对回归或自回归模型的随机扰动项进行建模。若ARCH模型可以写成下面的形式：

$h_t={\alpha }_0+{\alpha }_1{\epsilon }_{t-1}^2+\cdots +{\alpha }_q{\epsilon }_{t-q}^2+{\theta }_1{h}_{t-1}+\cdots +{\theta }_p{h}_{t-p}$ (2)

$h_t={\alpha }_0+{\displaystyle \underset{i=1}{\overset{q}{\sum }}{\alpha }_i}{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{q}{\sum }}{\theta }_j}{h}_{t-j}^2$ (3)

则称序列服从GARCH(p,q)过程。一般地，GARCH(1,1)模型就能很好地描述大量的金融时间序列数据 [5] 。

3. SV-t模型

在分析序列时，金融市场收益率序列与正态分布相比，通常表现出更大的峰度，而且有更厚的尾部，这就是尖峰厚尾现象。在SV模型的研究过程中，通常假定扰动项服从不同的分布来适应不同情况下的研究。SV-t模型，即扰动项 ${\epsilon }_t^2$ 服从t分布的SV模型，通过对SV-N模型的模型假设部分进行修改，即可得到SV-t模型的一般形式即：

$R_t={\epsilon }_t{\text{e}}^{\frac{h_t}{2}},{\epsilon }_t~\text{i}\text{.i}\text{.d}t\left(\text{0,1,}\omega \right)$ (4)

$h_t=\mu +\phi \left(h_{t-1}-\mu \right)+{\gamma }_t,{\gamma }_t~N\left(0,{\sigma }^2\right)$ (5)

与SV-N模型一致，其中 $R_t$ 是第t日的收益， $h_t$ 是第t日的对数波动。 $h_t$ 服从一阶自回归过程， $\mu$ 为常数， $\phi$ 为对数波动的持续性参数，用于刻画收益率当前波动对未来波动的影响，如果 $\left|\phi \right|<1$ ，那么SV-t模型的协方差是平稳的。SV-t模型中的随机扰动项 ${\epsilon }_t$ 服从自由度为ω的t分布， ${\epsilon }_t$ 和 ${\gamma }_t$ 不相关。

4. 实证分析

4.1. 数据的选择和处理

本文以上证综指和深证指数2016年1月至2019年5月的日股收盘价为基础，剔除了两市由于节假日以及不同的交易日等原因产生的无法匹配重合的数据后，得到832组数据，所有数据均来源于同花顺IFIND数据库。为了保证数据的平稳性，对上海证券综合指数的日收盘价(H)和深圳证券综合指数的日收盘价(Z)取对数为LH和LZ，而后差分得到两市收益序列 [6] ：

$R_{h,t}=\ln h_t-\ln h_{t-1}=\ln \left(\frac{h_t}{h_{t-1}}\right)$ (6)

$R_{z,t}=\ln z_t-\ln z_{t-1}=\ln \left(\frac{z_t}{z_{t\text{-}1}}\right)$ (7)

用R软件做出两市收益序列图：

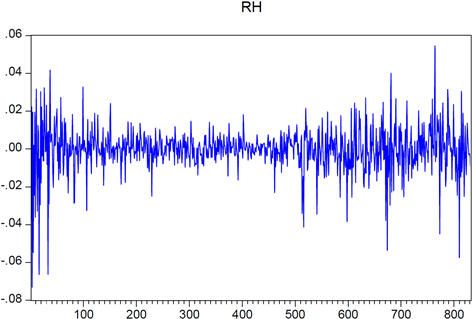
Figure 1. Return sequence diagram of shanghai composite index

图1. 上证综指收益率序列图

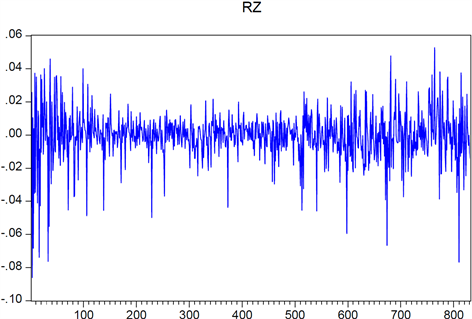
Figure 2. Shenzhen composite index return sequence chart

图2. 深圳综指收益率序列图

图1、图2为上证综指和深证综指的收益率波动图，两市波动趋势大体一致，且具有明显的波动聚集现象，例如在一头一尾的时间段内收益率的波动较大，而在中间从第170个观测值到第450个观测值这个时间段之内波动较小。

4.2. 数据描述性分析

数据描述见表1，图3、图4为两市收益率的柱形统计图，由图3、图4可知，上证综指日股收益率序列的均值(Mean)为−0.000170，标准差(Std.Dev)为0.011753，偏度(Skewness)为−1.024718，值为负数，这说明序列分布有长的左拖尾。峰度(Kurtosis)为9.811363，由于正态分布的峰值为3，因此远远大于其值。峰度值的比较表明该收益率序列具有尖峰厚尾的特征。JB统计量为1753.955，p值为0，拒绝原假设，即对服从正态分布的假设。同理对于深圳综指收益率，该收益率序列的平均值为−0.0004，标准差为0.0152，偏度为−0.9784，负值代表有长的左拖尾。峰度为7.9587，远远高于正太分布的峰值3，故说明该收益序列也有着尖峰厚尾的特征。

4.3. 考察序列的平稳性

本文采用ADF单位根检验两收益率序列的平稳性，得到如表2结果。

Table 1. Statistical table of data description

表1. 数据描述统计表

Table 2. ADF unit root inspection results

表2. ADF单位根检验结果表

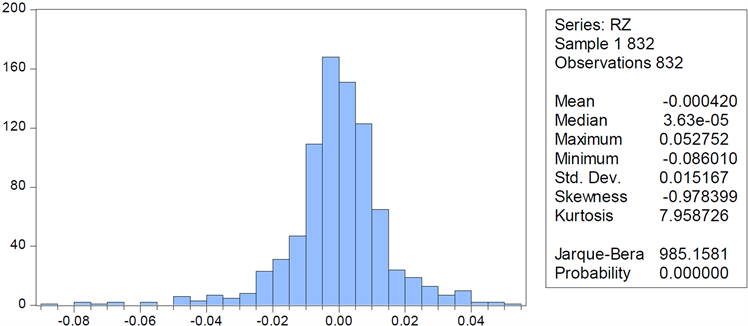
Figure 3. Descriptive chart of shanghai composite index return rate

图3. 上证综指收益率描述性统计图

Figure 4. Descriptive statistic of the Shenzhen Composite Index’s yield

图4. 深证综指收益率描述性统计图

根据单位根检验的结果，t统计量的值分别为−31.53745和−30.17459，均大于0.01、0.05、0.1三个水平上的他统计量，对应p值均都接近0，故表明序列十分平稳 [7] 。

4.4. 序列的ARCH-LM效应检验

序列是否存在ARCH效应，最常用的方法是拉格朗日乘数法，即LM检验。通过Eviews8.0进行检验，得到的两种检验结果如表3：

Table 3. ARCH effect test results

表3. ARCH效应检验结果

在第一行的F统计量在有限样本下不是精确分布，只能作为参考；第二行是统计量值以及检验的相伴概率。在上表中， ${\chi }^2$ 检验的相伴概率p值为0.0263，小于显著性水平0.05，拒绝原假设，序列存在ARCH效应 [8] 。

4.5. 序列的自相关以及偏自相关检验

从图5中可以看出，序列的自相关和偏自相关系数均落入两倍的估计标准差内，且Q-Stat所对应的p值均大于置信度0.05，故序列在5%的显著水平上不存在显著的自相关性。而由图6可以看出，两个收益序列是呈现尖峰厚尾以及服从非正态分布的特征。

Figure 5. Correlation test result chart

图5. 相关性检验结果图

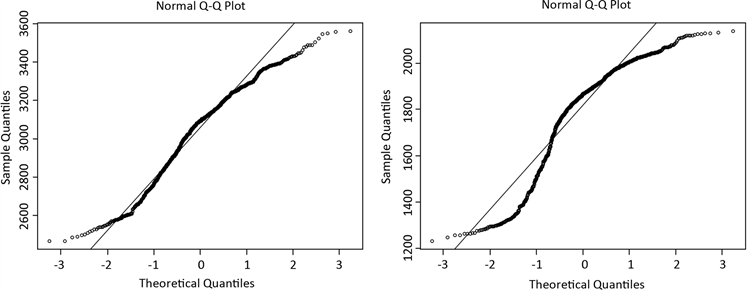
Figure 6. QQ chart of return rate of shanghai composite index and Shenzhen composite index

图6. 上证综指和深证综指收益率QQ图

4.6. GARCH模型实证

最为常用的GARCH模型有三种，分别是GARCH(1,1)，GARCH(1,2)，GARCH(2,1)。三种模式的检验结果如表4。

基于以上三个模型的比较，GARCH(1,1)所有的系数都通过检验，效果较好。接下来使用EGARCH模型进行深证收益率序列参数估计，结果如表5所示。

Table 4. Comparison of test results of three models

表4. 三种模型检验结果比较表

Table 5. Parameter estimation of Shenzhen composite index return series

表5. 深证综指收益率序列参数估计表

模型的参数均显著，说明序列具有杠杆性，可以近一步加入“ARCH-M”，来检验EGARCH模型，检验结果如表6：

Table 6. ARCH-M test results of Shenzhen composite index return sequence

表6. 深证综指收益率序列ARCH-M检验结果表

由结果可知，系数不显著，说明不存在ARCH-M过程。而后取不同滞后阶数对模型做出验证，验证结果如表7所示。

Table 7. Table of estimated results for different orders of Shenzhen composite index return series

表7. 深证综指收益率序列不同阶数情况下的估计结果表

在各种lag值情形下，F统计量均不显著，说明模型已经不存在ARCH效应。由于前文提到，收益率的描述统计中发现统计的正态分布检验没有通过，可以试图做残差服从t分布的Eviews建模。结果如表8所示，结果p值结果表明均通过检验。

Table 8. Parameter estimation of Shenzhen composite index return series

表8. 深证综指收益率序列参数估计表

4.7. SV模型实证

对于SV-t模型，为保证其收敛性，采用以不同初始值的两条马尔可夫链进行迭代，并设置其退火期为40,000，即先对每个参数进行40,000次迭代，将退火期舍弃掉再进行40,000次迭代，则可以得到参数的模拟结果以及运算时间。对于SV-t模型，其需要估计的参数为： $\mu ,\phi ,\tau ,\omega$ ，参照国外学者的设定，其中设定 $\phi =2{\phi }_1-1$ ，那么各参数的先验分布为：

$\begin{array}{l}\mu \sim N\left(0,100\right)\\ {\phi }_1\sim Beta\left(20,1.5\right)\\ \tau \sim Gamma\left(2.5,0.025\right)\\ \omega \sim {\chi }^2(8)\end{array}$

实证结果如图7、表9所示。

Table 9. Estimation results of parameters of MCMC algorithm in SV-T model

表9. SV-T模型MCMC算法各参数估计结果

Figure 7. bgr results of MCMC algorithm in SV-T model

图7. SV-T模型MCMC算法bgr结果图

由通过winbugs软件得出结果可知，φ的绝对值小于1，再次印证了上文通过GARCH模型收益率中存在着异方差这一结果。

5. 结论与建议

5.1. 主要结论

收益率序列存在着异方差性。改深证综指收益率有“尖峰厚尾”和波动聚集现象，不服从正态分布。风险对收益率的影响不够显著 [9] 。

指数收益率中存在杠杆性。投资者对该指数收益率下跌的反映往往高于相同程度收益上涨的反映，即收益率的下跌更容易出现强烈波动，对市场的冲击影响也更强 [10] 。

5.2. 主要建议

1) 信息披露等相关制度的健全要不断加强

要使得证券市场变得更加成熟，健全信息披露就变为重中之重。前文也提到了，由于证券市场受很多非理性因素影响存在比较明显的波动聚集的现象。市场不稳且具有不测变数，及时性有效性的信息披露必不可少。如果证券市场的一些基础相关信息能够得到及时的披露并且完整的更新，则能够让大家更好地实时了解当前证券市场运行状态，同时还可以充分发挥市场的功能。

2) 加强市场化建设，减少政府干预

在我国，政府较擅长于用“第三只手”对市场进行宏观调控，然而就是因为“第三只手”的存在，由于外界干预而导致市场内部运行的平衡得到了破坏。因此证券市场的波动性原因以及市场上的供需关系多加许多外在影响因素——政府干预。因此，若相关政府只是起到监管证券市场的合法性，为证券交易搭建一个稳定安全且平台，营造一个公平宏正的交易环境，而不是过多干预，那么就能避免产生额外的风险。

3) 加强对投资者的教育

越来越多的证券投资者都偏向于散户，并非具有全面而又扎实的理论基础，缺乏相关金融的知识导致他们可能盲目跟风，将目光专注于短操作，从而也放大了证券市场的金融风险，也容易造成金融市场的动乱。因此，投资者应该学习相关金融知识，树立正确的投资理念，培养善于洞察长期市场的能力，从而使得投资变得更加理性。

4) 加强证券市场法制建设

目前，我国的证券市场法治建设相关制度还不够完全，存在着很多的缺陷，例如存在运用不法手段幕后操纵、恶性竞争、非公平正义的交易等等，扰乱市场秩序，造成了严重的负面影响，助长了不良风气。因此要不断加强市场的法制化建设，规范交易行为迫在眉睫。