1. 引言
锚板作为一种重要的抗拔基础形式,因其结构简单且造价经济,而广泛应用于浮式海洋结构、输电线塔、高耸结构物、边坡挡墙等工程领域中。锚板种类较多,按照形状可将其分为条形锚板、圆形锚板与矩形锚板,按照埋深可将其分为浅埋锚板与深埋锚板。其中,锚板的极限抗拔承载力是锚板基础设计的重点与核心,而抗拔承载力的大小则主要取决于锚板的破坏机制。锚板抗拔承载力一直是锚板研究热点问题。在过去的几十年中,前人对锚板的极限承载力问题进行过较系统的研究。丁佩民,肖志斌等 [1] [2] 基于不同密实砂土中模型锚板上拔试验结果,结合以往的研究成果,系统研究了锚板承载能力的影响因素及锚板荷载位移特性,并按照从条形锚板到矩形锚板、从竖直锚板到倾斜锚板的思路,引入形状系数和倾斜系数,提出了便于工程应用的砂土中浅埋锚板统一抗拔极限承载力计算公式,提出了锚板抗拔位移计算方法。王栋等 [3] 基于大变形有限元分析了均质黏土中圆形锚板的极限抗拔力。刘君、于龙等 [4] [5] 基于弹塑性有限元对正常固结不排水黏土中的条形锚板、均质饱和黏土中圆形锚板的承载特性进行了数值模拟。舒恒等 [6] 采用有限元法并结合Hill稳定条件分别对无重和有重地基中条形锚板的极限承载力进行了研究,能够更好预测地基失稳范围和潜在失稳区域。余生兵,黄茂松等 [7] [8] [9] 提出了基于旋转块体集极限分析上限方法及块体集上限法,并分别对不排水黏土中深埋条形锚板及砂土中条形锚板的抗拔性能进行了数值分析。姚敬宇 [10] 采用PIV测量技术,对砂上中多节螺旋锚变形场进行了研究分析,通过对变形场的研究,确定了多节螺旋锚周围土体破坏形状的控制因素以及锚板间距对于多节螺旋锚基础承载力的影响,为多节螺旋锚基础极限抗拔力的预测提供了参考依据。解全一,张宏博等 [11] 分别对基于有限差分的数值计算法和室内模型试验确定的锚板极限承载力进行了分析对比,探讨了锚板承载力的影响因素。
在过去50多年来,许多学者研究了不同形状锚板的抗拔承载力,但是,大多数研究主要集中在传统锚板在静力荷载作用下的工作性状上。课题组在归纳整理深埋和浅埋锚板工作机理及流土机制的基础上,提出了串联式锚板锚固技术。并基于单锚板和串联式锚板室内模型试验结果,对比研究了单锚板和串联式锚板承载性状。利用FLAC 3D有限差分软件,建立了串联式双锚板的拉拔性状数值模拟模型,获得了上拔力–上拔位移关系曲线,并对其影响因素进行了探讨。
2. 串联式锚板的构造及优点
所谓“串联式锚板”就是将二块及以上的锚板用一根拉杆将其串在一起,锚板可以水平、竖直或倾斜埋设。它与传统意义上的锚板相比,具有如下优点:
1) 具有承载力高,可调性强,能有效控制和调整支挡结构或构筑物的位移。可通过施加预应力来控制与调整结构的位移及优化结构内力分布。
2) 能有效降低“群锚效应”。对于采用锚板联合其它支挡结构处理高填方的情况,能有效减少锚板层数,增大锚板的竖向间距,避免锚板相互干扰,从而降低“群锚效应”。
3) 施工简单,经济性好。在同高度、同一根拉杆上设置多个锚板,施工方便,经济性能好。
3. 室内模型试验
试验概况和试验方法
室内试验模型试验在长 × 宽 × 深 = 5米 × 3米 × 3米的基槽中进行。试验前,在模型槽的底部填500 mm厚的黏性土,再将单锚板及串联式双锚板固定在模型槽中,然后分层填筑黏性土。分层填筑时,采用长为600 mm、直径为500 mm的混凝土圆柱进行碾压,用密实度作为填筑控制指标,填筑前通过压实试验确定单层压实高度、压实遍数。模型试验制作完成后,静置2周后进行抗拔试验。由室内常规试验测得填土的土工参数分别为:土的压缩模量
,内摩擦角φ = 19.5˚,黏聚力c = 9.8 kPa,土的重度γ = 18.6 kN/m3。
锚板由钢板制作,平面尺寸为300 mm × 300 mm的方形锚板,模型锚板的厚度为10 mm,这样的厚度足够可以认为锚板为刚性的。在模型锚板平面的几何中心钻孔,在上拔试验时穿入直径为12 mm的圆钢拉杆,端部用螺栓扣住。圆钢拉杆表面涂漆,可以将拉杆在土中部分的摩阻力忽略。串联式锚板由二块锚板串联而成,上下锚板间距为1.0 m。为对比研究串联式锚板与单锚板的抗拔性状,串联式锚板的下锚板埋深与单锚板相同,埋深为2.5 m;串联式锚板的上锚板埋深1.5 m。
加载装置由主梁、位移测量装置、千斤顶、荷载传感器构成(如图1所示)。根据规范 [12] 荷载通过千斤顶分级施加,由扣在锚板上的钢拉杆对锚板施加上拔力。先估计锚板的极限抗拔力,定出加载等级,每级荷载按照预估极限抗拔力的1/10施加,加载完成后每隔10 min进行1次位移读数,相邻两级荷载之间读数次数不少于3次,当一级荷载连续3次读数范围内位移总量不超过0.1 mm时方可施加下一级荷载。在接近极限抗拔力时,应适当减小荷载分量,按照预估极限荷载的1/15~1/20施加。当施加荷载逐渐接近极限抗拔力时,如果位移增量不断增加或者突然增大,说明锚定板已经失稳,应以前一级荷载作为锚定板的极限承载力。
4. 数值模拟
4.1. 网格划分及边界条件
本数值计算采用FLAC3D有限差分法软件进行数值模拟。计算模型中的钢拉杆采用锚索单元模拟;锚板采用shell单元进行模拟;土体采用实体单元模拟。计算区域取3 m × 3 m × 2.5 m。边界约束条件为:底部边界(z = 0.0 m)所有点沿x,y和z方向的速度为零,侧面x = 0.0 m、3.0 m所有点的x方向速度为零及y = 0.0 m、3.0 m所有点的y方向速度为零。

Figure 1. Schematic diagram of indoor model test
图1. 室内模型试验示意图
4.2. 本构模型及计算参数
数值模拟中土的本构关系采用弹塑性模型和相关联的流动法则、Mohr-Coulomb屈服准则。计算参数为:锚板弹性模量E = 2.0 × 105 MPa,锚板密度ρ = 7800 kg/m3。其余土工参数与室内模型试验土工参数相同。
5. 上拔力–竖向位移关系及破坏模式
图2为锚板上拔力与竖向位移关系的实测与数值模拟对比曲线。由图2可以看出,数值模拟结果与模型试验结果吻合较好,这说明本文建立的数值模拟模型是合理可靠的。同时,从图中可看出:串联式锚板的抗拔承载力远大于传统的单锚板承载力。

Figure 2. Uplift force-displacement curve
图2. 上拔力–位移关系曲线
室内模型试验发现:对于传统的单锚板,在上拔力达到极限抗拔力时,地表的最大隆起量仅为1.3 mm,呈现出深埋锚板的破坏特征;对串联式双锚板,地表最大隆起量仅为1.9 mm,其地表最大隆起量略大于单锚板,这主要是因为上锚板锚深仅为1.5米所致,但总体上讲,地表隆起量与锚板上拔位移相比很微小,也可以认为串联式双锚板同样呈现出深埋锚板的破坏特征。因此,串联式锚板的破坏模式主要取决于下锚板的埋设深度。
数值模拟结果表明,对于下锚板为深埋的情况,串联式锚板之间存在临界间距,其临界间距为4~6 L (L为锚板长边尺寸),当锚板间距小于临界间距,下锚板附近的土体局部剪切破坏区贯通到上锚板时,会产生群锚板效应,从而降低锚板的抗拔承载力;对于下锚板为浅埋锚板的情况,串联式锚板上拔力–竖向位移关系曲线与传统的单锚板几乎接近,上锚板几乎不起作用。因此,串联式锚板只有深埋,至少保证最下层锚板深埋,才能有效提高锚板的抗拔承载能力。
图2为锚板上拔力–竖向位移关系曲线。由图2可看出:无论是串联式或是传统的单锚板,其上拔力–竖向位移关系荷载近似双曲线。其锚板从施加上拔荷载到最终破坏,可以分为三个阶段(如图2中1,2,3所示):1) 弹性压缩阶段,荷载较小时,锚板上方一定范围内的土体处于弹性压缩阶段,上拔力–竖向位移关系曲线为近似直线段,位移增加速率缓慢。当到达该阶段的末尾时,上拔力达到极限抗拔力约50%;2) 局部剪切阶段,锚板边缘附近的土体中出现局部剪切破坏区,锚板的位移开始不断增大,上拔力–竖向位移关系渐渐趋向水平,这一阶段上拔力达到极限抗拔力约80%~90%;3) 剪切破坏阶段,随着上拔力的进一步增加,微小的上拔力增量会引起位移的剧烈增长,对于浅埋锚板,土体中出现贯穿到土表面的整体剪切破坏面,到达极限抗拔力时,锚板急剧上拔伴随土表面隆起,对深埋锚板情况,锚板附近的土体局部剪切破坏,反映在上拔力–竖向位移的关系上是上拔力保持不变而位移持续增长,并且锚板的上拔对土体表面没有什么影响。
6. 串联式锚板抗拔承载力影响因素分析
6.1. 锚板间距对承载力的影响
图3为保持串联式锚定板中下锚定板埋深2.5 m不变的条件下,上下锚板的间距分别为0.5 m、1 m、1.5 m时,锚板上拔力–竖向位移关系曲线。由图3可看出,在下锚板埋深保持不变的条件下,上锚板的锚深从1.0米~1.5米~2.0米,其抗拔承载力并不随上锚板锚深的增加而增加,上锚板的锚深从2.0米减小到1.5米,即锚板间距从0.5米增加到1.0米,其抗拔承载力增加幅度较大,但上锚板的锚深从2.0米减小到1.0米,即锚板间距从0.5米增加到1.5米,其抗拔承载力反而降低。这说明在下锚定板埋深不变的情况下,串联式锚板的抗拔承载力不仅与上锚板的埋深有关,同时与上下锚板间距有关。课题组研究表明:对于深埋串联式锚板,其上下锚板临界间距S = (4~6) L。深埋串联式双锚板之所以存在临界间距是因为从竖平面上看,锚板破坏机构分为两个区域,即三角形区域和扇形区域,且均为变形区,当下锚板变形区达到或超过上锚板底面,则导致上下锚板存在变形区贯通,从而使下锚板承载力不能充分发挥。上下锚板变形区不贯通的最小距离称为上下锚板的临界间距。
6.2. 土的弹性模量及土的密度对承载力的影响
图4、图5分别为土体弹性模量及密度对锚板上拔力–位移关系的影响曲线。由图4、图5可看出:锚板抗拔承载力随土体弹性模量增加而增加,而土体密度的变化对锚板抗拔承载力影响不明显,这是因为该锚板埋深较大,属于深埋锚板所致。由此可推断,对于深埋锚板,通过增大锚板埋深来提高锚板抗拔承载力的效果不明显。
6.3. 土的黏聚力及内摩擦角对承载力的影响
图6、图7分别为土的黏聚力及内摩擦角对锚板上拔力–位移关系的影响曲线。由图6、图7可看出:锚板抗板承载力随土的黏聚力及内摩擦角增大显著增大。因此,提高土的抗剪强度能有效锚板的抗拔承载力。
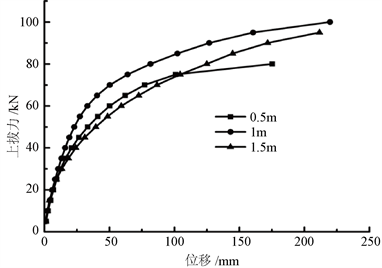
Figure 3. Effect of anchor plate spacing on uplift force-displacement relation
图3. 锚板间距对上拔力–位移关系的影响

Figure 4. Effect of elastic modulus of soil on uplift force-displacement relation
图4. 土的弹性模量对上拔力–位移关系的影响

Figure 5. Effect of soil density on uplift-displacement relation
图5. 土体密度对上拔力–位移关系的影响

Figure 6. Effect of cohesive forces of soil on uplift force-displacement relation
图6. 土的黏聚力对上拔力–位移关系的影响
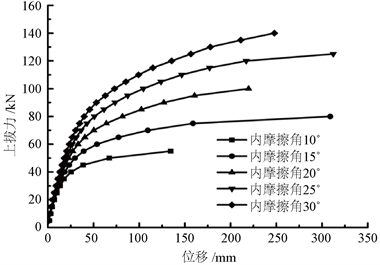
Figure 7. Effect of internal friction angles of soil on uplift force-displacement relation
图7. 土的内摩擦角对上拔力–位移关系的影响
6.4. 锚板尺寸对锚定板承载力的影响
图8为上下锚板间距保持1.0 m不变的条件下,不同尺寸的方形锚板上拔力–位移关系曲线。由图可看出,方形锚板面积从边长20 cm增大到30 cm,承载力提高的幅度最大,再进一步增大方形锚板面积,承载力提高的幅度降低。这主要是由于在上下间距一定的条件下,随着锚板尺寸增大,上下锚板间距接近或小于临界间距导致上下锚板产生群锚板效应,致使锚板承载力提高的幅度明显降低。
6.5. 锚板形状对锚定板承载力的影响
图9为上下锚板间距保持1.0 m不变的条件下,圆形锚板、方形锚板、不同宽度的矩形锚板上拔力–位移关系对比曲线。圆形锚板面积为0.09 m2,相当于方形锚板的面积。由图可看出,在锚板面积相同的条件下,圆形锚板的承载能力远大于方形锚板,同时,还可以看出,锚板从平面尺寸30 cm × 20 cm增大到30 cm × 30 cm,承载力提高的幅度最大,再进一步增大方形锚板面积,承载力提高的幅度显著降低。这主要是由于在上下间距一定的条件下,随着锚板尺寸增大,上下锚板间距接近或小于临界间距导致上下锚板产生群锚板效应所致。

Figure 8. Effect of sizes of anchor plates on uplift force-displacement relation
图8. 锚板尺寸对上拔力–位移关系的影响

Figure 9. Effect of shapes of anchor plates on uplift force-displacement relation
图9. 锚板形状对上拔力–位移关系的影响
7. 结论
本文在归纳整理深埋和浅埋锚板工作机理及流土机制的基础上,提出了串联式锚(碇)板锚固技术,并基于室内模型试验,结合数值模拟,研究了串联式双锚定板的拉拔性状及影响因素,获得如下结论。
1) 串联式双锚定板的承载能力远大于单锚定板,面积相同的圆形锚板的承载力远大于方形锚板。
2) 无论是单锚定板或是串联式双锚定板,上拔力–上拔位移关系的典型曲线为双曲线。
3) 土的强度参数对串联式双锚定板对上拔力–上拔位移关系影响明显。
4) 对于串联式双锚定板,在下锚板埋设深度一定,且为深埋锚板的条件下,土的重度对上拔力–上拔位移关系影响很小,同时,双锚板之间存在临界间距,当锚板间距大于临界间距,随着上锚板埋深增大,串联式双锚板的承载力增加,初步获得双锚板临界间距(4~6 L)。锚板临界间距的影响因素还有待于进一步详细研究。
致谢
感谢审稿人和编辑部提供的有益建议。
基金项目
国家自然科学基金资助项目(No. 51978260)。