一类时滞交通流模型的多稳定性研究

Multistability in Delay Car-Following Models

摘要: 众所周知，交通系统是一个十分复杂的非线性大系统，受到诸多因素的制约，建立一个能够准确描述系统特性的数学模型是一项极具挑战性的工作。时滞车辆跟驰模型是指包含司机反映时滞的车辆跟驰模型。本文在已有模型基础上分析了司机反映时滞对车辆跟驰模型复杂动力学行为的影响，如稳定、分岔、多稳定性及混沌等。通过数值模拟与理论分析，揭示了司机反映时滞这一个体特征在驾驶过程中的重要性。

Abstract: It is well-known that traffic system is a complex nonlinear large system. There are a great number of factors to influence the evolutionary behavior of the system. It is a challenging job to propose a mathematical model to accurately describe such a real system. In car following models of traffic dynamics, there exists a finite time for human drivers to process stimuli of preceding vehicles and make a decision. It is natural to give a detailed study of the mechanism about how time delays affect the traffic flow patterns and their evolutions. In this paper, we are interested in rich dynamical behavior in a class of nonlinear car-following models, including stability, Hopf bifurcations, multistability and chaotic behavior etc. Numerical simulation gives a solid verification of our findings.

1. 引言

揭示交流中所蕴含的复杂非线性行为(分岔、混沌等)是人们长期关注的重要课题。研究发现分岔是交通流中各种非线性因素耦合影响的重要表现形式：当系统中某些参数发生变化越过某个临界值时，交通流系统的拓扑结构发生变化，诱发均匀流与堵塞流之间相变。目前，对交通流中的分岔等复杂现象的研究大多集中在车辆跟驰模型，详见文献综述 [1] [2] 及其中参考文献。

值得一提的是，文献 [3] 提出如下具体模型

${\ddot{x}}_i\left(t+\tau \right)=\frac{a{\stackrel{\dot{}}{x}}_i^m\left(t\right)\left[{\stackrel{\dot{}}{x}}_{i-1}\left(t\right)-{\stackrel{\dot{}}{x}}_i\left(t\right)\right]}{{\left[x_{i-1}\left(t\right)-x_i\left(t\right)\right]}^l}+b\left[x_{i-1}\left(t\right)-x_i\left(t\right)-L_i\right]$ (1)

其中 $m=0,a,b>0$， $L_i$ 为两车之间的实际存在的安全间距， $x_i\left(t\right),{\stackrel{\dot{}}{x}}_i\left(t\right),{\ddot{x}}_i\left(t\right)$ 分别为车队中车辆的位置、速度及加速度； $d_i\left(t\right)=x_i\left(t\right)-x_{i+1}\left(t\right)$ 为相邻两辆车之间的车头间距， $\tau$ 为驾驶员延时反应时间，一般为0.4~1.6秒， $a,b$ 分别表示对车速变化和车头间距变化的反应灵敏度系数。同时还分析由3辆车组成的系统的稳定性及其Hopf分岔特性，揭示了不同的系统时滞量(驾驶员反映时间)和不同的安全间距对系统稳定域的影响。

本文将揭示时滞所引起的系统多稳定性、高余维分岔等，并提出了一类新的非线性模型，模拟了混沌交通流等复杂动力学行为。

根据现有文献，多稳定性(Multistability)是生物学家Kenneth W. Nicker-Son在讨论多稳定蛋白质的生物功能时提出来的 [4]。该词现已在多个领域广泛应用，如声光非线性系统、学习算法、神经网络模型、寡头经济模型、人口模型以及传染病动力学模型的多稳定性研究等。从动力系统角度看，多稳定性是指系统多个平衡点或/与多个周期解(极限环)、多个混沌吸引子的同时存在性。系统最终的运动形式往往与系统地最初状态(初始条件)有关：初始条件不同，而最终的状态不一样(相空间中存在多个吸引子和相应多个吸引域)。这是复杂系统普遍存在的一种现象，如(高维或无穷维)系统中因多种分岔现象而出现多个平凡吸引子或(与)混沌吸引子的同时存在性，以及混沌映射中存在的无穷多周期层次结构等。而本文将揭示时滞车辆跟驰模型同样存在此类现象。

当L_i ≡ L时 [3]，可理解为同质结构，即单一车道上跟随车辆与首车车况、车型相同；而当L_i互异时系统为异质结构，即单一车道上跟随车辆与首车车况、车型不同，鱼龙混杂。

2. 模型描述与多稳定性分析

假设车队中车辆数，并设头车以某一速度匀速前进，即 $\stackrel{\dot{}}{x}=v_0,\ddot{x}\equiv 0$，则模型(1)可写成如下四维非线性自治时滞动力系统形式：

$\begin{array}{l}\text{d}y/\text{d}t=[v_1\left(t\right);-a{v}_1\left(t-\tau \right)/d_1\left(t-\tau \right)-b\left(d_1\left(t-\tau \right)-L_1\right);v_2\left(t\right);a{v}_{\text{1}}\left(t-\tau \right)/d_{\text{1}}\left(t-\tau \right)\\ +b\left(d_{\text{1}}\left(t-\tau \right)-L_{\text{1}}\right)-a{v}_{\text{2}}\left(t-\tau \right)/d_{\text{2}}\left(t-\tau \right)-b\left(d_{\text{2}}\left(t-\tau \right)-L_{\text{2}}\right)]\end{array}$ (2)

其中 $y={\left[\begin{array}{cccc}{d}_1& v_1& d_2& v_2\end{array}\right]}^{\text{T}}$， $v_i\left(t\right)={\stackrel{\dot{}}{x}}_i\left(t\right)-{\stackrel{\dot{}}{x}}_{i+1}\left(t\right)$ 同时我们还将观察到如下系统存在的混沌交通流及其多稳定现象：

$\begin{array}{l}\text{d}y/\text{d}t=[v_1\left(t\right);-a{v}_1\left(t-\tau \right)/d_1\left(t-\tau \right)-b\left(d_1\left(t-\tau \right)-L_1\right)-k{\left(d_{\text{1}}\left(t\right)-L_{\text{1}}\right)}^{\text{5}};v_2\left(t\right);\\ a{v}_{\text{1}}\left(t-\tau \right)/d_{\text{1}}\left(t-\tau \right)+b\left(d_{\text{1}}\left(t-\tau \right)-L_{\text{1}}\right)-a{v}_{\text{2}}\left(t-\tau \right)/d_{\text{2}}\left(t-\tau \right)\\ -b\left(d_{\text{2}}\left(t-\tau \right)-L_{\text{2}}\right)+k{\left(d_{\text{1}}\left(t\right)-L_{\text{1}}\right)}^{\text{5}}-k{\left(d_{\text{2}}\left(t\right)-L_{\text{2}}\right)}^{\text{5}}]\end{array}$ (3)

由文献 [3] 或直接计算可知，系统平衡点为 ${\left(L_1,0,L_2,0\right)}^{\text{T}}$，时滞临界值为

${\tau }_j^{*}=\frac{\arctan \frac{a\omega }{b{L}_i}+\pi j}{\omega },j=0,1,2,\cdots$

其中

$\omega =\sqrt{\frac{a^2+\sqrt{a^4+4L_i^4{b}^2}}{2L_i^2}},i=1,2.$

当时滞 $\tau >{\tau }_{\text{0}}^{*}$ 系统不稳定，当时滞 $\tau <{\tau }_{\text{0}}^{*}$ 系统在平衡点附近局部稳定。

进一步验证Hopf分岔的横截性条件，可计算得当 $\tau ={\tau }_j^{*}$ 时

${\Re \frac{\text{d}\lambda }{\text{d}\tau }|}_{\tau ={\tau }_j^{*}}=\frac{-a{\omega }^2\left(a-b{L}_i\tau -2L_i\omega \sin \left(\omega \tau \right)\right)+L_{i}b{\omega }^2\left(2L_i\cos \left(\omega \tau \right)-a\tau \right)}{{\left(a-b{L}_i\tau -2L_i\omega \sin \left(\omega \tau \right)\right)}^2+{\omega }^2{\left(2L_i\cos \left(\omega \tau \right)-a\tau \right)}^2},$

及

${\Re \frac{\text{d}\lambda }{\text{d}a}|}_{\tau ={\tau }_j^{*}}=\frac{-{\omega }^2\left(2L_i\cos \left(\omega \tau \right)-a\tau \right)}{{\left(a-b{L}_i\tau -2L_i\omega \sin \left(\omega \tau \right)\right)}^2+{\omega }^2{\left(2L_i\cos \left(\omega \tau \right)-a\tau \right)}^2},$

${\Re \frac{\text{d}\lambda }{\text{d}b}|}_{\tau ={\tau }_j^{*}}=\frac{-\left(a-b{L}_i\tau -2L_i\omega \sin \left(\omega \tau \right)\right)}{{\left(a-b{L}_i\tau -2L_i\omega \sin \left(\omega \tau \right)\right)}^2+{\omega }^2{\left(2L_i\cos \left(\omega \tau \right)-a\tau \right)}^2}.$

(a) (b)

Figure 1. Critical values of losing stability by (double) Hopf bifurcations in system (2) as b varies and a is fixed

图1. 当b变化而a固定时，系统(2)中的(双)Hopf分岔失稳的临

(a) (b) (c)

Figure 2. Critical values of losing stability by (double) Hopf bifurcations in system (2) as τ varies

图2. 当τ变化时，系统(7.2)中的(双)Hopf分岔失稳的临界值

图1画出了当参数a固定后中临界时滞与参数b及车间安全距离的相互影响。观察分析可知：有时较小的车间安全距有较高的稳定性，而有时较大的车间安全距才有较高的稳定性。之间的转化(临界状态)可用多稳定性或高余维分岔来解释。这里主要表现为双Hopf分岔。如图1(b)所示当a = 18.3时L_i = D = 16所对应的临界曲线与D = 26所对应的临界曲线在b = 0.5附近相交，从而若所给系统中L₁ = 16，L₂ =26，则在对应两曲线交点邻域出现双Hopf分岔。类似现象也可以在图2中其它参数值所对应的临界曲线交点处观察到：D = 6所对应曲线与另外两曲线均相交。因此若系统(2)或(3)中L₁ = 6，L₂ = 16 (或26)，则在两曲线交点处出现双Hopf分岔。从另外一个角度说明了这种高余维现象的普遍存在性。比较图2中三幅图(τ = 0.5, 1, 1.5)还可发现，随着反应时间增长，参数平面上稳定域范围大幅缩小，从而说明驾驶员的快速反应有利于系统安全性能的提高。

图3从数值的角度验证了Hopf分岔所满足的横截性条件，并且由所给数值值(>, =或<0)，说明图1与图2中所画临界曲线的内侧区域稳定，外侧不稳定，与已有理论分析及数值结果吻合。

Figure 3. Transversality conditions

图3. 横截性条件

3. 进一步分析

文献 [3] 已指出模型(2)中很难数值观测到稳定的极限环。为此我们研究方程(3)。在图4中取 $L_1=L_2=16\text{m}$ , a=6, b= 0.8,τ=0.99, k=0.08及初值 $y\left(t\right)\equiv {\left[\begin{array}{cccc}16.7& 0.01& 17.9& 0.01\end{array}\right]}^{\text{T}}$ , $t\in \left[-\tau ,0\right]$。即设在开始

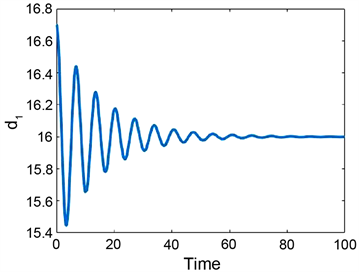
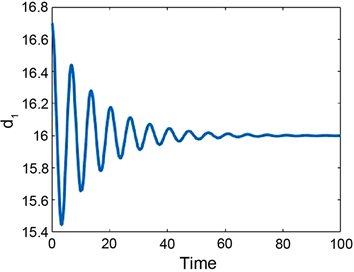
时间段内，第1、2辆车和第2、3辆车之间的车头间距分别为16.7 m和17.9 m，相对速度差均为0.01 m/s。从图4的仿真计算结果可见，系统出现了混沌交通流。图5比较了模型(2)与(3)之间动力学差异，其中L₁ = 16, L₂ = 26 m，初始值与图4同。前者(L₁ = 16)对应子系统参数位于稳定域内，而后者参数位于不稳定域。我们看到了均匀流与周期流的同时存在性。两系统(2)与(3)均出现同样现象，但频率有很大差异。可归结为车辆加速的差异，前者为低速情形，而后者为高速情形。但需要进一步运用非线性动力系统方法解释相应机理。而关于此类多稳定性现象，文 [3] 没有研究讨论。

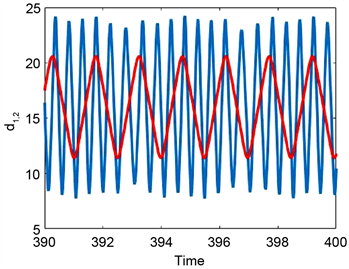
(a) (b)

Figure 4. Chaotic behavior in system (3) with a = 6, b = 0.8, L₁ = 16, L₂ = 16, τ = 0.99,k = 0.08 under the initial condition $y\left(t\right)\equiv {\left[\begin{array}{cccc}16.7& 0.01& 17.9& 0.01\end{array}\right]}^{\text{T}}$ , $t\in \left[-\tau ,0\right]$ . (a) Time series; (b) Phase portrait

图4. 系统(3)中的混沌行为在初始条件 $y\left(t\right)\equiv {\left[\begin{array}{cccc}16.7& 0.01& 17.9& 0.01\end{array}\right]}^{\text{T}}$ 下，a = 6，b = 0.8，L₁ = 16，L₂ = 16，τ= 0.99，k = 0.08， $t\in \left[-\tau ,0\right]$。(a) 时间序列；(b) 相图

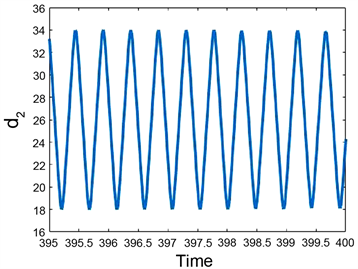(a) (b)

Figure 5. Multistability in system (2) and (3) for a = 6, b = 0.8, L₁ = 16, L₂ = 26, τ = 0.3 under the initial condition $y\left(t\right)\equiv {\left[\begin{array}{cccc}16.7& 0.01& 17.9& 0.01\end{array}\right]}^{\text{T}}$ , $t\in \left[-\tau ,0\right]$ . (a) System (3.2), k = 0; (b) System (3.3), k = 0.08

图5. 系统(2)和(3)中的多稳态性，其中a= 6, b =0.8, L₁ = 16, L₂ = 26, τ = 0.3，及初始条件 $y\left(t\right)\equiv {\left[\begin{array}{cccc}16.7& 0.01& 17.9& 0.01\end{array}\right]}^{\text{T}}$ , $t\in \left[-\tau ,0\right]$。(a) 系统(3.2)，k = 0；(b) 系统(3.3)，k = 0.08

4. 结论

本文发现了一类时滞交通流模型中存在的多稳定性现象，并提出一类新的非线性模型，模拟了混沌交通流等复杂动力学现象。尽管模型(3)可以看成模型(2)的高阶扰动模型，在适当条件下均可诱发均匀流与堵塞流的相变，但周期震荡频率有很大差异，需要进一步运用非线性系统理论加以研究。

本文没有深入分析混沌这一重要非线性特征，可以通过考察初值敏感依赖性及计算最大Lyapunov指数与分形维数等加以验证，文 [5] 的研究方法提供了很好的参考。通过数值模拟揭示了系统高余维分岔(双Hopf)的存在。进一步进行理论分析，是一个有趣的课题。由于其高维特性，相应动力学行为分析有难度。运用时滞微分方程理论 [6] [7] [8] [9]，揭示交通堵塞背后的各种非线性现象产生的内在机制，如交通拥堵的形成和演化机理，以及交通堵塞的分类等问题，将是我们今后研究的重点。

基金项目

山东省自然科学基金资助(ZR2015AL004)及国家自然科学基金资助(No. 61977004)。