“电路、信号与系统”中的相量和频域分析教学方法研究

Phasor Analysis and Frequency Domain Analysis in Circuits, Signals and Systems

摘要: 在“电路基础理论”和“信号与系统”两门课程中，基于相量法的电路正弦稳态分析与系统频域分析都是十分重要的内容，两者之间存在着深刻的内在联系，然而初学者不易把握。本文在剖析相量法和频域法的本质、异同和教学过程所遇到问题的基础上，提出了一个全新的授课思路，希望能改进“电路、信号与系统”课程的教学时效。

Abstract: In the courses of “Circuit Basic Theory” and “Signal and System”, the sinusoidal steady-state analysisof circuit based on phasor methodand the frequency domain analysis of system both are important contents, and there is a deep internal relation between them, which few students can really understand. Based on the analysis of the essence, similarities and differences of the phasor method and the frequencydomain method，as well as the problems encountered during teaching activities, this paper puts forward a new teaching idea, hoping to improving the teaching effectiveness for the course of “Circuits, Signals and Systems”.

1. 引言

对于高等学校电子信息类专业来说，“电路基础理论”和“信号与系统”是两门十分重要的学科基础课程。其中，基于相量法的电路正弦稳态分析和系统频域分析都是十分重要的内容，两者之间有着深刻的内在联系。然而，多年的教学经验表明，学生不易将这两部分内容联系起来，比如，不能把“信号与系统”中电路的频域模型、频响特性与“电路基础理论”中的相量模型、网络函数联系起来。在“信号与系统”中应用频域分析方法求解分析电路稳态问题时，往往机械运用傅氏变换和逆变换方法得到输出信号，不能从本质上把握系统频响特性的物理意义，难以提高实际分析解决电路问题的能力。另一方面，将“电路基础理论”和“信号与系统”两门课程合并成“电路、信号与系统”课程时也需要深入研究教学方法。

本文在剖析传统“电路基础理论”课程中的相量法和和“信号与系统”中频域分析方法的本质、异同和教学中遇到的问题的基础上，针对“电路、信号与系统”课程提出一种全新的授课思路，希望让学生在相对比较少的课时情况下，掌握电路稳态问题的分析方法，理解系统频响特性的实际意义。

2. 传统电路理论课程中相量法

传统的电路基础理论课程一般首先在纯电阻电路的环境里介绍电路的基本规律、基本定理和分析方法。有的教材 [1] 把这部分内容称为“直流电路”。但笔者更愿意采用“电阻电路”这一提法。纯电阻电路本质上是一个“即时、无记忆”系统，描述其输入、输出关系的数学模型是代数方程(组)。在这种“零阶”系统环境下，讨论电路的基本规律、定理和分析方法都十分方便且容易被接受。事实上，不仅仅是直流激励，交流信号激励下电阻电路的分析方法都是一样的。因为，对于一个“零阶”线性系统，输入、输出或者说各处信号之间的关系是一个“比例”关系。另一方面，所谓直流电路是指激励为直流信号的电路，原则上电路中除了电阻，还可以有电容、电感等“记忆”元件。只是，在直流信号激励下，电容表现为断路(电阻无穷大)、电感表现为短路(电阻为零)，因此输入、输出或者说各处信号之间依然为“比例”关系。所以，纯电阻电路和直流电路可以归类为“静态电路”，其输入、输出信号之间的关系是一个取决电路结构和参数的“比例”关系。

含有电感、电容等“记忆”元件，在非直流信号激励下的电路便被称为“动态电路”。动态电路在数学模型上表现为一阶以上的微分方程(组)；稳定的动态电路在功率信号的激励下将产生瞬态响应和稳态响应。由于直接由电路微分方程求解其稳态响应是个繁琐的过程，于是便有了基于相量法的正弦稳态分析。一般地，电路基础理论的教材都是从正弦信号的三要素，即幅值、频率、相角开始引入正弦信号的相量表示，通过讨论电阻、电感和电容端电压与其中电流的关系引出感抗和容抗，介绍相量形式的KCL和KVL，进而给出电路复阻抗以及电路的相量模型。相量法大大方便了动态电路的稳态分析，但传统相量法的教学过程琐碎、繁杂，需要消耗较多的课时资源、且难以形成更具有普遍意义的理论方法。

3. 信号与系统课程中的频域分析方法

“信号与系统”对信号和系统给出了更一般化的描述，信号的时域、频域与S域分解，系统的时域、频域与S域分析，依次展开，层层推进，概念丰富、逻辑清晰、理论完整，无疑在更高的层面上提供了分析包括电路系统在内的动态系统的理论方法。然而，多年的教学实践中注意到，学生对于把握信号系统框架中时域、频域与S域三类不同分析方法的本质与内在关系感到困难，比较容易停留在纯粹的数学变换层面；并且对“信号与系统”和“电路基础理论”中相关联的内容，如系统稳态响应分析以及系统频响特性，与“电路基础理论”中正弦稳态分析部分的关系认识不到位，导致花费了大量的课堂资源，却没有收到应有的教学效果。例如，已知系统频率响应函数 $H\left(j\omega \right)$ 如图1所示，当 $f\left(t\right)=2+4\cos \left(5t\right)+4\cos \left(10t\right)$ 时，求系统响应。

Figure 1. Amplitude and phase frequency characteristics of a system

图1. 某系统幅频和相频特性

有学生采用傅里叶级数法。首先写出

$f\left(t\right)=2+4\cos \left(5t\right)+4\cos \left(10t\right)={\displaystyle \underset{n=-2}{\overset{2}{\sum }}2{\text{e}}^{jn5t}}$,

所以、 $F_n=\{\begin{array}{l}2,n=0,\pm 1,\pm 2\\ 0,其余\end{array}$，再由 $Y_n={H\left(j\omega \right)|}_{\omega =\text{5}n}{F}_n$，得

$\begin{array}{c}y\left(t\right)={\displaystyle \underset{n=-2}{\overset{2}{\sum }}{Y}_n{\text{e}}^{jn5t}}\\ =0+{\text{e}}^{-j\left(5t-{90}^{\circ }\right)}+2+{\text{e}}^{j\left(5t-{90}^{\circ }\right)}+0\\ =2+2\cos \left(5t-{90}^{\circ }\right)\end{array}$

也有学生采用傅里叶变换法。因为， $F\left(j\omega \right)=4\pi {\displaystyle \underset{n=-2}{\overset{2}{\sum }}\delta \left(\omega -5n\right)}$，通过 $Y\left(j\omega \right)=H\left(j\omega \right)F\left(j\omega \right)$，可得

$Y\left(j\omega \right)=4\pi \left[0.5{\text{e}}^{j{90}^{\circ }}\delta \left(\omega +5\right)+\delta \left(\omega \right)+0.5{\text{e}}^{-j{90}^{\circ }}\delta \left(\omega -5\right)\right]$,

再取傅立叶逆变换得

$y\left(t\right)={\text{e}}^{-j\left(5t-{90}^{\circ }\right)}+2+{\text{e}}^{j\left(5t-{90}^{\circ }\right)}=2+2\cos \left(5t-{90}^{\circ }\right)$.

以上两种方法都具备数学上的严谨和完美，却未能凸显系统频率响应函数 $H\left(j\omega \right)$ 的物理意义。事实上，从图1可以清楚地看到，系统的直流增益为1、角频率5 rad/s处的增益为0.5，相移为负的0.5π rad，而角频率10 rad/s处的增益为零。因此，可以直接得到系统的响应 $y\left(t\right)=2+2\cos \left(5t-{90}^{\circ }\right)$。我们把这种方法称为幅频相频法。相较傅里叶级数法和傅里叶变换法，幅频相频法更清晰地反映了系统频率响应特性的本质。

“信号与系统”作为一门独立的课程是在“电路基础理论”之后 [2]，其中系统频域分析部分与“电路基础理论”中的相量法以及相关的阻抗、网络函数等概念之间的有着深刻的内在联系。然而教学中发

现，能够把这两个方法联系起来灵活应用的学生不多。例如，如图2所示周期方波电压源 $u_s\left(t\right)$ 作用于RL电路，试求电流 $i\left(t\right)$ 的前五次谐波。

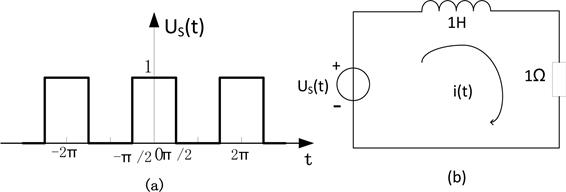
Figure 2. Periodic square wave signal acts on the RL circuit

图2. 周期方波信号作用于RL电路

部分学生的解题过程如下：

1) 求出 $u_s\left(t\right)$ 的前五次谐波表达式：

${u_s\left(t\right)|}_{0,\sim ,5}=\frac{1}{2}+\frac{2}{\pi }\cos \left(t\right)-\frac{2}{3\pi }\cos \left(3t\right)+\frac{2}{5\pi }\cos \left(5t\right)$ ;

2) 列写微分方程 $i^{\prime }\left(t\right)+i\left(t\right)=u_s\left(t\right)$ ；

3) 设 $i\left(t\right)$ 的前五次谐波为

$C_0+C_1\cos \left(t\right)+C_2\sin \left(t\right)+C_3\cos \left(3t\right)+C_4\sin \left(3t\right)+C_5\cos \left(5t\right)+C_6\sin (5t)$

4) 代入微分方程求得7个待定系数;

5) 最后得到 $i\left(t\right)$ 的前五次谐波为

$\frac{1}{2}+\frac{1}{\pi }\cos \left(t\right)+\frac{1}{\pi }\sin \left(t\right)-\frac{1}{15\pi }\cos \left(3t\right)-\frac{1}{5\pi }\sin \left(3t\right)+\frac{1}{65\pi }\cos \left(5t\right)+\frac{1}{13\pi }\sin (5t)$

以上过程计算繁琐。若采用幅频相频法则会很简洁，即首先写出系统的频率响应函数 $H\left(j\omega \right)=\frac{I\left(j\omega \right)}{U_s\left(j\omega \right)}=\frac{1}{1+j\omega }$，然后分别计算其在 $\omega =0,1,3,5$ 时的幅值与相角，便可方便地求出 $i\left(t\right)$ 的前五次谐波。事实上，以上方法与“电路基础理论”中的相量法在本质上是一致的，关键是如何让学生认识到。

4. 电路、信号与系统课程中的系统稳态分析

以上分别分析了基于相量法和频域分析的系统稳态分析方法，以及目前教学实践中存在的问题。下面讨论在“电路、信号与系统”课程中，如何通过一个全新的授课思路，让学生在相对比较少的课时条件下，真正掌握电路稳态问题的分析方法，理解系统频响特性的实际意义。

“电路基础理论”与“信号与系统”两门课的结合点在于动态电路的分析方法。笔者之前提出了“电路、信号与系统”课程的总体组织框架 [3]，即，电路篇、信号篇和系统篇。基本思想是，在电路篇里在电阻电路的环境下介绍电路所特有的基本规律、定理和分析方法；在动态电路部分先介绍基本的动态元件(电感、电容等)的伏安关系，动态电路微分方程的列写以及响应的构成，强调动态电路所具有的动态响应和稳态响应过程。电路正弦稳态分析则从电路篇中移出，合并到系统篇中的系统稳态分析部分，在频域分析方法之后引出。在信号篇里，以线性叠加定理为切入点，系统介绍信号的时域、频域以及s域的分解。在强调积分、傅氏和拉氏三大变换的物理意义的同时为解决动态系统分析提供必要的数学工具。在系统篇里则打破时域、频域以及s域分析的传统框架，将系统篇分为系统动态分析和稳态分析两个部分。灵活应用数学工具为系统分析服务。比如在系统动态分析部分，直接把时域和S域方法打通。引入电路的S域模型，强调指出，在S域模型下，之前电路篇中的电阻电路的理论、分析方法可以完全移植过来，从而方便地解决动态电路的动态分析。在动态过程分析中强调系统过渡过程和稳态响应的概念，为系统稳态分析做好铺垫。

系统稳态分析的重要概念是系统的频率响应特性，其次是明确所谓系统的稳态响应本质上是稳定系统在功率信号激励下的响应，也就是系统对正弦信号的响应的合成。为防止学生落入纯数学推演的陷阱，将系统在正弦信号激励下的响应与系统频率特性的关系直接以“定理”的形式给出，然后通过三种途径加以证明。

定理：频率响应特性为 $H\left(j\omega \right)$ 的系统在 $f\left(t\right)=A\cos \left({\omega }_{0}t+{\phi }_0\right)$ 激励下的稳态响应为 $y\left(t\right)=A|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]$。

证明一：设系统的输入为 $f_1\left(t\right)=A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}$ 、冲激响应为 $h\left(t\right)$，则系统的输出为

$\begin{array}{c}{y}_1\left(t\right)=f_1\left(t\right)\ast h\left(t\right)={\displaystyle {\int }_{-\infty }^{+\infty }A{\text{e}}^{j\left[{\omega }_0\left(t-\tau \right)+{\phi }_0\right]}}h\left(\tau \right)\text{d}\tau \\ =A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}{\displaystyle {\int }_{-\infty }^{+\infty }A{\text{e}}^{-j{\omega }_0\tau }}h\left(\tau \right)\text{d}\tau \\ =A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}H\left(j{\omega }_0\right)\\ =A|H\left(j{\omega }_0\right)|{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}{\text{e}}^{j\phi \left({\omega }_0\right)}\\ =A|H\left(j{\omega }_0\right)|{\text{e}}^{j\left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]}\end{array}$

由于 $f\left(t\right)=A\cos \left({\omega }_{0}t+{\phi }_0\right)$ 是 $f_1\left(t\right)=A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}$ 的实部，所以系统的输出 $y\left(t\right)$ 也是v的实部，即、 $y\left(t\right)=A|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]$。

证明二：设系统的输入为 $f_1\left(t\right)=\cos \left({\omega }_{0}t\right)\epsilon \left(t\right)$ 、传递函数为 $H\left(s\right)$，则系统输出 $y_1\left(t\right)$ 的拉氏变换为

$Y_1\left(s\right)=\frac{s}{s^2+{\omega }_0^2}H\left(s\right)=Y_{1h}\left(s\right)+\frac{1}{2}\frac{1}{s-j{\omega }_0}H\left(j{\omega }_0\right)+\frac{1}{2}\frac{1}{s+j{\omega }_0}H\left(-j{\omega }_0\right)$

其中， $Y_{1h}\left(s\right)$ 对应的是输出中暂态响应部分的拉氏变换，其余对应的是稳态响应 $y_{1ss}\left(t\right)=|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+\phi \left({\omega }_0\right)\right]$。同理，输入为 $f_{\text{2}}\left(t\right)=\sin \left({\omega }_{0}t\right)\epsilon \left(t\right)$ 时，稳态响应为 $y_{2ss}\left(t\right)=|H\left(j{\omega }_0\right)|\sin \left[{\omega }_{0}t+\phi \left({\omega }_0\right)\right]$。故，当 $f\left(t\right)=A\cos \left({\omega }_{0}t+{\phi }_0\right)\epsilon \left(t\right)$ 时，稳态响应为 $y_{ss}\left(t\right)=A|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]$。

证明三：设系统的输入为 $f_1\left(t\right)=\cos \left({\omega }_{0}t\right)$ 、频响特性为 $H\left(j\omega \right)$，则系统输出 $y_1\left(t\right)$ 的傅氏变换为 $\begin{array}{c}{Y}_1\left(j\omega \right)=H\left(j\omega \right)\pi \left[\delta \left(\omega -{\omega }_0\right)+\delta \left(\omega +{\omega }_0\right)\right]\\ =\pi \left[H\left(j{\omega }_0\right)\delta \left(\omega -{\omega }_0\right)+H\left(-j{\omega }_0\right)\delta \left(\omega +{\omega }_0\right)\right]\end{array}$ 所以， $y_1\left(t\right)=|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+\phi \left({\omega }_0\right)\right]$。

同理，当输入为 $f_{\text{2}}\left(t\right)=\sin \left({\omega }_{0}t\right)$ 时，响应为 $y_{\text{2}}\left(t\right)=|H\left(j{\omega }_0\right)|\sin \left[{\omega }_{0}t+\phi \left({\omega }_0\right)\right]$。故，当输入为 $f\left(t\right)=A\cos \left({\omega }_{0}t+{\phi }_0\right)$ 时，响应为 $y\left(t\right)=A|H\left(j{\omega }_0\right)|\cos \left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]$。

顺便指出，从以上的证明过程可以看到，正是由于在信号篇里解决了所有相关的数学问题，在系统篇里才可以方便、灵活地加以应用，同时也便于学生体会时域、频域和S域的本质和三者之间的联系。

在解决了一般线性系统的稳态响应后，再回头看电路的正弦稳态分析方法。首先，在动态电路的时域模型的基础上引入电路的频域模型，强调指出，之前电路篇中的电路理论、分析方法同样可以完全移植到频域模型来。同时考虑到相量法在很多教材和文献中都会出现，有必要对读者和学生有个交代，而且在讲完频域方法后，可以以一个全新的角度，更加简洁地引入电路的相量模型。从上面的证明一可以

看到，由于 $f\left(t\right)=A\cos \left({\omega }_{0}t+{\phi }_0\right)$ 是 $A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}$ 的实部，我们可以记输入、输出的相量形式分别为 $\stackrel{\dot{}}{F}=A{\text{e}}^{j\left({\omega }_{0}t+{\phi }_0\right)}$ 、 $\stackrel{\dot{}}{Y}=|H\left(j{\omega }_0\right)|A{\text{e}}^{j\left[{\omega }_{0}t+{\phi }_0+\phi \left({\omega }_0\right)\right]}$。这样就可以写出正弦信号激励下系统输入、输出的相量形式的表达式 $\stackrel{\dot{}}{Y}=\stackrel{\dot{}}{F}H\left(j{\omega }_0\right)$。

回到传统电路理论中的正弦稳态分析。正弦与相量形式的电流、电压表达式为： $i\left(t\right)=\sqrt{2}I\cos \left({\omega }_{0}t+{\phi }_{i0}\right)$ 、 $u\left(t\right)=\sqrt{2}U\cos \left({\omega }_{0}t+{\phi }_{u0}\right)$ 和 $\stackrel{\dot{}}{I}=I{\text{e}}^{j{\phi }_{i0}}=I\angle {\phi }_{i0}$ 、 $\stackrel{\dot{}}{U}=U{\text{e}}^{j{\phi }_{u0}}=U\angle {\phi }_{u0}$。对比两种相量记法，在电路理论中相量的模是其有效值，相角只记初相角而略去了角频率。之前电阻电路中的电路理论、分析方法同样可以完全移植到动态电路的相量模型中来。两种相量记法在本质上是一致的，都可以方便的表达系统在正弦信号激励下的稳态响应。

基于以上对系统频域分析方法和电路理论中相量法内在关系的深入剖析，在最近的两个教学周期里，我们实施了一个全新的教学方法，即、略去传统电路理论中的正弦稳态分析部分，在系统频域分析理论下讲清系统在正弦激励下的响应之后，引入一般意义的相量表达，接着介绍电路理论中的相量法。应用这种方法，只需增加一个学时便可完成相量法的讲授。相较传统讲授方法所需的5个学时，显著地减少了授课学时；同时我们发现这样的讲授方法让学生们进一步看清了一般系统频域分析与电路系统相量分析之间的内在联系并加以灵活应用。

5. 总结

本文剖析了电路基础理论中基于相量法的正弦稳态分析和信号系统中的频域分析方法，针对“电路、信号与系统”课程，提出一个全新的授课思路。两个周期的教学实践表明，应用这个授课思路，能够大幅减少授课学时，同时又让学生认识到一般系统频域分析与电路系统相量分析之间的联系并加以灵活应用，从而改进了相关内容的教学效果、提高了教学时效。

“电路基础理论”和“信号与系统”两门课程连接点在于动态电路的分析。在多数“电路基础理论”教材中，是以分析对象、分析任务为“导向”，在需要的地方引入相应的数学知识，使学习者往往因为零散出现的数学问题而感到困惑；而“信号与系统”更偏重于理论方法的系统完整性，使得一些学习者不自觉地陷入数学推演里，从而忽视了理论的工程背景及其实际应用。因此，当把“电路基础理论”和“信号与系统”两门课程整合到一起时，应该在一个更高的层面审视两门课程的理论体系，寻求更加合理、更加高效的课程组织体系和教学方法，让学生在更少的课堂学时资源的情况下，更好地掌握电路与信号系统的核心理论并能够灵活地应用于解决实际问题。本文提出的关于频域分析和相量法的教学方法便是研究两门课程内在关系的一个实例。

参考文献

NOTES

^*第一作者。