基于改进小波阈值的GPS观测数据降噪方法研究

Study on GPS Observation Data Denoising Method Based on Improved Wavelet Threshold

摘要: GPS观测数据中混入的噪声会导致定位精度大大降低。针对传统的小波阈值降噪方法在阈值函数和阈值选取方面的不足，设计了一种新型半软阈值函数，利用涡流搜索算法和广义交叉验证实现了分层阈值的自适应确定。改进后的方法不需要先验知识，操作简单，鲁棒性好。数值仿真验证了该方法可以显著降低GPS定位误差。

Abstract: The noise mixed in the GPS observation data will lead to a significant reduction of positioning accuracy. For the shortcomings of traditional wavelet threshold denoising methods in threshold function and threshold selection, a new semisoft threshold function is designed. The hierarchical threshold is determined adaptively by vortex search algorithm and generalized cross-validation. The improved method does not require a prior knowledge, and is easy to use, yet of strong robustness. Numerical simulations verify that this method can significantly reduce the GPS positioning error.

1. 引言

全球定位系统(Global Positioning System, GPS)具有自动化观测、全天候连续作业、控制点不需要通视等特点，能够为全球用户提供低成本、高精度的三维位置、速度和定时等导航信息，因此被广泛应用于交通、建筑、通信、电力、军事等领域 [1]。

由于测量仪器(如卫星摄动、卫星数据更新率)、测量环境(如大气层延迟、多路径效应)以及人为因素(如数据处理方法)的影响，GPS接收机接收到的信号不可避免地混入了部分噪声，使得定位结果出现一定的失真，其中以高斯白噪声最为常见 [2] [3]。从信号频谱的角度来看，GPS信号中的有用成分集中分布在低频范围内，而噪声成分集中分布在高频范围内，两者存在一定的交集。这就使得单纯的低通或高通滤波方法无法有效地分离有用成分和噪声成分 [4]。

目前，GPS观测数据的降噪方法主要包括基于Kalman滤波的方法 [5] 和基于小波分析的方法 [6]。其中，Kalman滤波需要提前知道准确的系统数学模型和噪声统计，这在大部分情况下是很难做到的，不准确或错误的模型和噪声统计会导致滤波效果降低甚至发散。而小波降噪凭借良好的时频局部化特性，可以从不同尺度对信号进行分解处理，在有效降噪的同时，能够尽量保留信号的有用成分，因而受到了很多研究人员的青睐 [7] [8] [9] [10]。

小波降噪的关键是如何提取有用成分的小波系数，剔除噪声成分的小波系数。利用阈值筛选小波系数，即小波阈值降噪方法，由于原理简单、操作方便、计算量小、降噪效果好以及能够较好地保留反映原始信号特征的尖峰点等优点，在实际工作中得到了广泛应用 [11] [12]。

在小波阈值降噪过程中，最重要的环节就是小波系数调整准则的确定和阈值的选取。调整准则是对高于或低于阈值的小波系数进行不同的处理，即确定一个合适的阈值函数。而选取的阈值过小，则噪声不能完全消除，反之则信号的某些细节特征会被滤除。综合来说，这两方面设置直接关系到信号降噪的质量。

传统的阈值函数主要分为硬阈值函数、软阈值函数或半软阈值函数 [13]。其中，硬阈值函数在阈值处不连续，会造成重构信号的自激振荡，影响重构信号的光滑性，当小波系数绝对值大于阈值时，硬阈值函数只是单纯地保留原始小波系数，混杂在内的部分噪声分量没有被有效剔除，容易产生较大的方差；而软阈值函数不存在间断点，得到的重构信号较为光滑，但是它对绝对值大于阈值的小波系数采取恒定压缩的方式，偏离了噪声分量随小波系数的递增而逐渐减小的趋势，会滤掉一些有用的高频分量，使得重构信号与原始信号存在一定的偏差；半软阈值函数对于很多信号的降噪效果要优于硬阈值函数或软阈值函数，但是在阈值附近的过渡不够平滑。阈值主要分为全局阈值和分层阈值。相比于全局阈值，分层阈值更加灵活可控，适应能力更强，因此降噪效果往往更好。但是传统的分层阈值确定需要一定的先验知识(如噪声方差)，这在实际工作中是很难实现的。

针对传统阈值函数和分层阈值确定的局限，本文设计了一种改进的半软阈值函数，利用涡流搜索算法(Vortex Search, VS) [14] 结合广义交叉验证准则(Generalized Cross-Validation, GCV) [15] 自适应地确定分层阈值，有效降低了GPS观测数据的定位误差。本文首先简要介绍了小波阈值降噪的基本原理，接着描述了半软阈值函数的改进和分层阈值的确定，通过数值模拟验证了所提出的方法在GPS观测数据降噪方面的有效性，最后对本文工作进行了总结。

2. 小波阈值降噪基本原理

小波阈值降噪的基本思想是原始信号经过小波变换后的信号系数仅在某些尺度、某些位置上有较大的值，而噪声的小波系数在所有尺度、所有位置上都有较平均的值。通过估计各个尺度上噪声的幅度值，并参照信号的幅度值，设置阈值，去掉噪声的小波系数，保留信号的小波系数，即可去除噪声。这种方法的优点是计算量较小，噪声几乎完全得到抑制，并且反映原始信号特征的尖峰点得到很好的保留。

如图1所示，小波阈值降噪的一般处理步骤为：

① 小波变换

一维的离散加性噪声信号模型可以表示为：

$h\left(n\right)=s\left(n\right)+\epsilon \left(n\right)$ (1)

其中 $h\left(n\right)$ 为含噪信号， $s\left(n\right)$ 为原始信号， $\epsilon \left(n\right)$ 为噪声信号， $n=1,2,\cdots ,N$ ，N是信号的长度。

对 $h\left(n\right)$ 作离散小波变换，得到

$\tilde{h}\left(m,n\right)=\tilde{s}\left(m,n\right)+\tilde{\epsilon }\left(m,n\right)$ (2)

其中 $\tilde{h}\left(m,n\right)$ 、 $\tilde{s}\left(m,n\right)$ 和 $\tilde{\epsilon }\left(m,n\right)$ 分别为 $h\left(n\right)$ 、 $s\left(n\right)$ 和 $\epsilon \left(n\right)$ 在第m层上的小波系数， $m=1,2,\cdots ,M$ ，M是小波变换的最大分解层数。

② 阈值降噪

按照一定的准则，选择适当的阈值，对每一层的小波系数进行量化处理。

③ 逆小波变换

对处理后的小波系数进行逆小波变换，得到降噪后的重构信号。

Figure 1. Procedures of wavelet threshold denoising

图1. 小波阈值降噪步骤

3. 半软阈值函数的改进

常用的阈值函数包括硬阈值函数、软阈值函数和半软阈值函数，将 $\tilde{h}\left(m,n\right)$ 写作 ${\tilde{h}}_{m,n}$ ，则硬阈值函数的表达式如下

${\widehat{\stackrel{˜}{h}}}_{m,n}=\{\begin{array}{l}0\left|{\tilde{h}}_{m,n}\right|<T\\ {\tilde{h}}_{m,n}\left|{\tilde{h}}_{m,n}\right|\ge T\end{array}$ (3)

软阈值函数的表达式为

${\widehat{\stackrel{˜}{h}}}_{m,n}=\{\begin{array}{l}0\left|{\tilde{h}}_{m,n}\right|<T\\ \mathrm{sgn}\left({\tilde{h}}_{m,n}\right)\left(\left|{\tilde{h}}_{m,n}\right|-T\right)\left|{\tilde{h}}_{m,n}\right|\ge T\end{array}$ (4)

而半软阈值函数可以表示为

${\widehat{\stackrel{˜}{h}}}_{m,n}=\{\begin{array}{l}0\left|{\tilde{h}}_{m,n}\right|<T_1\\ \mathrm{sgn}\left({\tilde{h}}_{m,n}\right)\frac{T_2\left(\left|{\tilde{h}}_{m,n}\right|-T_1\right)}{T_2-T_1}{T}_1\le \left|{\tilde{h}}_{m,n}\right|\le T_2\\ {\tilde{h}}_{m,n}\left|{\tilde{h}}_{m,n}\right|>T_2\end{array}$ (5)

其中T、T₁和T₂都是阈值。

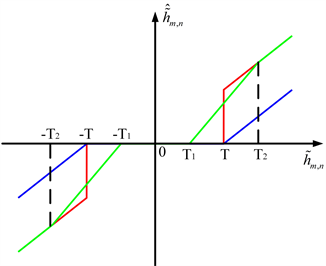
Figure 2. Diagram of traditional threshold functions (red line represents hard threshold function, blue line represents soft threshold function, and green line represents semisoft threshold function)

图2. 传统阈值函数示意图(红线表示硬阈值函数，蓝线表示软阈值函数，绿线表示半软阈值函数)

从图2中可以看出，一方面，硬阈值函数在 $\pm T$ 位置出现了间断点，数据的间断会使信号在重构时发生振荡，另一方面，当 $\left|{\tilde{h}}_{m,n}\right|$ 大于阈值时，硬阈值函数只是简单地保留小波系数，没有剔除其中的噪声，容易造成较大的方差；相对于硬阈值函数，软阈值函数有较好的连续性，有效地避免了振荡问题，但是对于 $\left|{\tilde{h}}_{m,n}\right|$ 大于阈值的小波系数，处理后的系数存在恒定偏差，某些表征边缘的原始信号小波系数和噪声一起收缩，造成重构信号的边缘和细节部分出现模糊失真；半软阈值函数的出发点是当 $\left|{\tilde{h}}_{m,n}\right|<T_1$ 时，小波系数全部对应噪声信号，在 $T_1$ 和 $T_2$ 之间是原始信号和噪声信号的小波系数混合区域，而当 $\left|{\tilde{h}}_{m,n}\right|>T_2$ 时，小波系数全部对应原始信号，这通常与实际情况比较吻合，因此半软阈值函数对于很多信号的降噪效果要优于硬阈值函数或软阈值函数。

一般来说，阈值函数在阈值附近要有比较好的平滑过渡带，即在噪声和信号的分界点之间要有较好的平滑过渡带，这样得到的信号会更接近自然信号。传统的半软阈值函数在这方面表现不甚理想，因此本文提出一种改进的半软阈值函数，将 $\tilde{h}\left(m,n\right)$ 写作 ${\tilde{h}}_{m,n}$ ，表达式如下

${\widehat{\stackrel{˜}{h}}}_{m,n}=\{\begin{array}{l}0\left|{\tilde{h}}_{m,n}\right|<T_{1,m}\\ {\tilde{h}}_{m,n}\left[\frac{1}{2}+\frac{1}{2}\cos \left(\frac{\left|{\tilde{h}}_{m,n}\right|-T_{2,m}}{T_{2,m}-T_{1,m}}\pi \right)\right]T_{1,m}\le \left|{\tilde{h}}_{m,n}\right|\le T_{2,m}\\ {\tilde{h}}_{m,n}\left|{\tilde{h}}_{m,n}\right|>T_{2,m}\end{array}$ (6)

其中， $T_{1,m}$ 和 $T_{2,m}$ 是第m层上的阈值。如图3所示，与传统半软阈值函数相比，改进函数在 $\pm T_{1,m}$ 和 $\pm T_{2,m}$ 位置附近过渡更加平滑。

Figure 3. Comparison of semisoft threshold functions

图3. 半软阈值函数对比示意图

4. 分层阈值的确定

VS算法是最近提出的一种新型元启发式单解优化算法。如图4所示，它的灵感来源于搅动液体产生的涡流现象，可以实现搜索行为的探索和开发之间良好的平衡。该算法通过使用一种自适应步长调整方案的搜索行为模拟涡流现象，具有操作简单和搜索能力强的优点，不需要设置过多参数，只需考虑迭代次数、候选解集大小及搜索空间上下限等参数，其搜索能力超过了单解的模拟退火算法、模式搜索算法和群解的人工蜂群算法。

阈值主要分为全局阈值和分层阈值。前者指的是对各层小波系数采用统一的阈值进行处理，后者指的是对各层小波系数分别采用不同的阈值进行处理。相比于全局阈值，分层阈值明显更加灵活可控，适应能力更强，因此实际工作中的降噪效果往往更好。在本文中，为了进一步提升分层阈值的适应能力，在不需要任何先验知识的条件下，利用VS算法尽可能地确定最优的分层双阈值 $T_{1,m}$ 和 $T_{2,m}$ 。

利用VS算法获取最优解需要一个判定标准。最优阈值的判定准则采用GCV，即第层的目标函数定义为

$\text{GCV}\left(T_{1,m},T_{2,m}\right)=\frac{N\cdot {\displaystyle \underset{n=1}{\overset{N}{\sum }}{\left({\tilde{h}}_{m,n}-{\widehat{\stackrel{˜}{h}}}_{m,n}\right)}^2}}{{\left({\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(1-\left|\frac{{\widehat{\stackrel{˜}{h}}}_{m,n}}{{\tilde{h}}_{m,n}}\right|\right)}\right)}^2}$ (7)

Figure 4. Diagram of optimization process for vortex search algorithm

图4. VS算法寻优过程示意图

通过求解GCV的最小值来确定最优 $T_{1,m}$ 和 $T_{2,m}$ 。

5. 数值模拟

本文基于MATLAB 2018b软件平台进行数值仿真。假定目标在水平面上运动，初始位置为(0, 0)，x方向和y方向的运动速度分别为20 m/s和5 m/s。GPS接收机的扫描间隔为1 s，扫描时间为50 s。首先在原始数据中分别加入信噪比(Signal to Noise Ratio, SNR)为30 dB、20 dB和10 dB的高斯白噪声，得到观测数据。接着利用本文提出的小波方法进行降噪处理，并和基于传统阈值函数(硬阈值函数、软阈值函数或半软阈值函数)的小波阈值降噪方法比较，综合验证本文所提出方法的有效性。此外，在小波基的选取方面，通常要考虑到其正交性、紧支性、对称性等特性。而在小波分解层数的确定方面，一般小波分解层数越多，越有利于信噪分离，但是失真导致的重构误差也越大。因此，通过大量仿真验证，发现选用db5小波基，并将小波分解层数设为4，对于不同的小波阈值函数均能取得较好的降噪效果。

为了定量比较不同方法的降噪效果，引入了均方根误差(Root Mean Square Error, RMSE)作为评判标准，定义为

$\text{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}\left[{\left({x^{\prime }}_n-x_n\right)}^2+{\left({y^{\prime }}_n-y_n\right)}^2\right]}}$ (8)

其中 $\left(x_n,y_n\right)$ 是原始数据， $\left({x^{\prime }}_n,{y^{\prime }}_n\right)$ 表示 $\left(x_n,y_n\right)$ 加噪后再做降噪处理得到的数据。

图5显示了不同降噪方法处理后的GPS观测数据与原始数据之间的RMSE。可以看出，随着SNR的降低，任何一种方法处理后的数据RMSE都逐渐增大。当噪声成分相同时，本文提出的方法降噪效果最好，降噪后的数据RMSE要小于其他方法处理后的结果。

以加入SNR为10 dB的噪声后的观测数据为例，原始数据、含噪数据和降噪数据对应的目标运动轨迹如图6所示。考虑到图面显示的清晰直观，这里只给出了本文所提出方法降噪后的结果。可以看出，与原始数据相比，含噪数据对应的目标轨迹偏差较大，而降噪后的目标轨迹与真实轨迹吻合较好，表明本文所提出的小波方法在该条件下表现良好，这也和定量计算的结果一致。

Figure 5. Comparison of RMSE for different denoising methods

图5. 不同降噪方法的RMSE比较

Figure 6. Comparison of target trajectories

图6. 目标运动轨迹对比

6. 结论

在实际工作中，GPS观测数据中不可避免地混入了一些噪声，对准确定位带来了不利影响。小波分析具有良好的时频局部化特性，可以有效分离GPS信号中的有用成分和噪声成分。本文设计了一种新型半软阈值函数，可以改善传统阈值函数的不足，利用VS算法和GCV准则自适应地确定分层阈值，突破了先验知识的局限。仿真结果表明，与传统的小波阈值降噪方法相比，本文提出的方法降噪效果更好，能够显著降低GPS观测数据的定位误差。

基金项目

本文受到气动噪声控制重点实验室2018年度开放课题(1801ANCL20180303)的资助。