基于质量守恒方程的高压油管压力控制研究

Research on Pressure Control of High Pressure Tubing Based on Mass Conservation Equation

摘要: 高压油管广泛应用于发动机制造，一种高效合理的高压油管压力控制方案，对推动发动机制造业和经济社会发展具有十分重要的意义。通过对高压燃油系统工作原理的研究，提出了一种新的高压油管压力控制方案。首先，根据高压油管进油和喷油质量守恒关系，分别推导出了高压油管在恒压和不恒压条件下的压强与时间的微分方程模型。其次，推导出了高压油管油泵凸轮柱塞运动的角速度计算公式。进一步，考虑到高压油管恒压条件下多个喷油嘴工作的情况，分别讨论了多个喷油嘴不同工作情况下的控制方案。最后，通过对数据进行拟合，检验了模型的准确性。数值结果表明，在恒定压力下单向阀每次开启时长为0.64 ms，高压泵凸轮柱塞角速度为2.7543 rad/ms。多个喷油嘴同时和不同时工作时，高压泵凸轮柱塞角速度大小分别为5.5086 rad/ms、1.37715 rad/ms。此外，本文根据结果制定了一种高压油管压力控制方案，为发动机高压油管的发展提供了理论依据。

Abstract: High-pressure tubing is widely used in engine manufacturing. An efficient and reasonable high- pressure tubing pressure control scheme is of great significance for promoting engine manufacturing and economic and social development. Through the research on the working principle of high-pressure fuel system, a new high-pressure fuel pipe pressure control scheme is proposed. Firstly, according to the mass conservation relationship between high-pressure oil pipe feeding and spraying, the differential equation model of pressure and time of high-pressure oil pipe under constant pressure and non-constant pressure conditions is derived respectively. Secondly, the formula for calculating the angular velocity of the cam plunger movement of the high-pressure tubing oil pump is derived. Further, considering the operation of multiple injectors under the constant pressure condition of high pressure tubing, the control schemes of different injectors under different working conditions are discussed respectively. Finally, the accuracy of the model was tested by fitting the data. The numerical results show that the constant value of the check valve is 0.64 ms at a constant pressure and the angular velocity of the high pressure pump cam plunger is 2.7543 rad/ms. When multiple injectors are working at the same time and at different times, the angular velocity of the high pressure pump cam plunger is 5.5086 rad/ms and 1.37715 rad/ms, respectively. In addition, based on the results, a high pressure fuel pipe pressure control scheme is developed, which provides a theoretical basis for the development of high-pressure fuel pipe.

1. 引言

内燃机对世界工业革命和社会经济发展起到了巨大的推动作用 [1]。燃油进入和喷出高压油管是许多燃油发动机工作的基础，燃油经过高压油泵进入高压油管,由喷油嘴喷出。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化，使得所喷出的燃油量出现偏差，从而影响发动机的工作效率以及工业制造业的经济效益。因此对高压油管压力控制的研究对于发动机制造业和经济社会的发展具有十分重要的意义。

在以往的研究中，许多学者分别对高压油管进行了不同的研究。在国内，1990年，赵学亭等人 [2] 对高压油管压力波和喷油器针阀升程进行测量。1991年，王美丽等人 [3] 对高压油管结构参数研究。1992年，殷子嘉等人 [4] 对高压油管中燃油压力波的传递速度测定。2003年，韦海燕等人 [5] 对高压油管压力波研究。2009年，黄立贤等人 [6] 对高压油管内应力研究。2013年，李丕茂等人 [7] 对高压油管内轨压和喷油脉宽研究。在国外，2005年，Zhang等人 [8] 对电控喷油器和钢轨空腔体积研究。2007年，L等人 [9] 对高压燃油管经常出现柴油机裂纹的泄漏研究。2009年，H等人 [10] 对喷油压力研究。HE等人 [11] 对高压共轨喷射系统控制研究。2011年，Liu等人 [12] 对共轨柴油机的喷油系统参数优化设计。2012年，S等人 [13] 对轨道压力控制器研究。2015年，L等人 [14] 对共轨压力控制器研究。在众多的研究中，高压油管结构参数和喷油针阀的研究和测量，解决了喷油的规律和特性等问题，但不能反映高压油管内部压力变化。对自增强处理工艺的研究，从硬件上提高了油管寿命，对喷油脉宽和空腔体积的研究，提出了压力波幅度与喷油脉宽的关系以及影响喷油率的因素。对喷油和高压共轨系统的研究以及不断优化高压油管参数，对稳定性和共轨压力进行了控制和调节，有效的预测系统燃油的喷射量。但无论是对于高压油管自身参数的研究，还是对共轨控制系统的研究。都忽略了高压油管内部压力的控制。燃油通过高压油泵和喷油嘴进出高压油管都会影响高压油管的压力控制，高压油管内部压力的变化进而又反作用于燃油进入高压油泵和从喷油嘴进出，进而使得所喷出的燃油量出现偏差，从而影响发动机的工作效率以及工业制造业的经济效益。因此，越来越多的学者对高压油管压力控制进行研究，希望提出一种合理的高压油管压力控制方案。

本文通过对高压油管压力控制的研究，提出了一种新的基于质量守恒方程的高压油管压力控制模型。赵学亭等人 [2] 和王美丽等人 [3] 解决了喷油规律和喷油特性的问题，但却忽略了间歇性工作过程会导致高压油管内压力的变化。殷子嘉等人 [4] 、韦海燕等人 [5] 、李丕茂等人 [7] 提出了压力波和喷油脉宽影响油管的工作，却没有给出两者之间明确的影响关系模型。黄立贤等人 [6] 、Zhang等人 [8] 、L等人 [9] 、Liu等人 [12] 对高压油管参数的研究，提高了油管的使用寿命，却没有涉及高压油管内部压力的变化。H等人 [10] 、HE等人 [11] 、S等人 [13] 、L等人 [14] 解决了共轨系统压力变化的控制系统，但没有考虑到油管内部会使得所喷出的燃油量出现偏差。要使高压油管内的压力尽可能稳定，则要保持管内燃油密度不会变化。根据质量守恒定律，在一个供油周期内，供油质量等于喷出燃油的质量。高压油泵每工作一次，喷油嘴工作一次。若管内压强增加,则对于高压油管而言，管内的气体压强会在一个很小的范围内波动。考虑到凸轮驱动柱塞由低压状态旋转至高压状态的过程，高压油管凸轮柱塞的角速度必须满足喷油嘴的工作要求。当多个喷油嘴工作时，在与单个喷油嘴喷油同样的时间内，柱塞的转动速率必须加快，喷油供油策略需要进行调整。本文通过建立的基于质量守恒方程的高压油管压力控制模型，从理论上详细讨论的高压油管压力变化与其他因素的关系，控制了高压油管压力的稳定，在计算机拟合的基础之上准确的模拟了高压油管工作时内部压力的变化，并提出了一种十分有效的高压油管压力控制方案。

2. 基于质量守恒方程的高压油管压力控制模型

(一) 高压油管恒压压力控制模型

燃油的压力变化量和密度变化量成正比。比例系数为 $\frac{E\left(P\right)}{\rho }$，与弹性模量E有关 [15]。本文通过对压

力变化量和密度变化量的分析，建立弹性模量随压强变化模型如下：

$E\left(p\right)=k{\text{e}}^{\lambda p}$ (1)

由此关系建立压力变化量 $\Delta P$ 与密度变化量 $\Delta \rho$ 关系模型：

$\text{d}P=k\text{d}\rho =\frac{E\left(P\right)}{\rho }\text{d}\rho$ (2)

考虑高压油管工作过程中存在的质量守恒：

$m_{in}+m_{old}=m_{out}+m_{now}$ (3)

又 $m_{old}=m_{now}$， $m_{in}=m_{out}$。建立进出气体质量相等的微分方程模型如下( ${\rho }_{160}=0.8712$ 为160 MPa下的密度)：

$\text{d}\rho =\frac{{\rho }_{160}CA\sqrt{\frac{2\left(P_A-P\right)}{{\rho }_{160}}}}{{\displaystyle \int \bar{v}\text{d}t}}\text{d}t$ (4)

建立了压力与时间关系微分方程模型得到：

$\text{d}P=\frac{k{\rho }_{160}CA\sqrt{\frac{2\left(P_A-P\right)}{{\rho }_{160}}}}{{\displaystyle \int \bar{v}\text{d}t}\cdot \exp \left(-\lambda P-\frac{{\text{e}}^{-\lambda P}}{k\lambda }-\frac{D}{k}\right)}\text{d}t$ (5)

(二) 高压油管不恒压压力控制模型

随着高压油管工作的进行，( $m_{in}+m_{old}$)一直在不断增加，( $m_{out}+m_{now}$)也在同步增加，记( $m_{out}+m_{now}$)为m。建立高压油管变动压力的微分模型如下( $m_{old}$ 是初始状态下管内的气体质量)：

$\{\begin{array}{l}\text{d}m=\sqrt{{\rho }_{160}}CA\sqrt{2\left[P_A+\frac{\ln \left(-\lambda k\ln \frac{m}{V+\bar{v}t}-\lambda D\right)}{\lambda }\right]}\text{d}t\\ m_0={\rho }_{100}V\end{array}$ (6)

由 $m_{in}=m_{out}$，建立出高压油管变动压力的微分模型：

$\text{d}P=\frac{k{\rho }_{0}CA\sqrt{\frac{2\times \left(P_A-P\right)}{{\rho }_0}}}{{\displaystyle \int \bar{v}\text{d}t}\cdot \exp \left(-\lambda -\frac{{\text{e}}^{-\lambda P}}{k\lambda }-\frac{D}{k}\right)}\text{d}t$ (7)

(三) 高压油管恒压单喷油嘴柱塞运动模型

考虑凸轮驱动柱塞由低压状态旋转至高压状态这个转一圈的过程，低压状态下，高压油泵的体积为 $V_b$，高压油泵在低压状态下气体的质量 $m_b$。高压状态下，残余体积为v mm³,残留气体的质量 $\Delta m$。进入高压油管中气体的质量为：

$m_{in}=m_b-\Delta m$ (8)

高压油管内气体的密度：

${\rho }_g=\frac{m_{in}+m_{old}}{V_{old}}$ (9)

引用高压油管工作过程中存在的质量等式：

$M_{in}+m_{old}=m_{out}+m_{now}$ (10)

由 $m_{old}=m_{now}$ 即 $M_{in}=m_{out}$。从而得出质量守恒模型：

$\{\begin{array}{l}{M}_{in}=n{m}_{out}\\ m_{in}=\text{d}\rho \text{d}v\end{array}$ (11)

建立针阀运动高度模型如下：

$h\left(t\right)=a{t}^5+b{t}^4+c{t}^3+d{t}^2+et+\epsilon$ (12)

建立喷油体积和时间的关系模型如下：

$V=\frac{1}{3}\ast \pi \ast \left(a{t}^5+b{t}^4+c{t}^3+d{t}^2+et+\epsilon \right)\ast \left(R^2+r^2+R\ast r\right)$ (13)

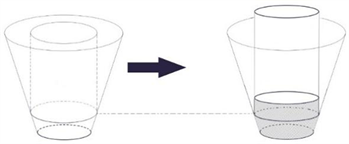
Figure 1. Dynamic working process and volume diagram of the injector

图1. 喷油嘴的动态工作过程及体积示意图

将喷油嘴的形状抽象补充成一个完整的圆锥，如图1所示，令喷孔半径为r，则喷孔到圆锥顶点的距离为：

$h_1=\frac{r}{\tan 9^{\circ }}$ (14)

设升值为h，则阴影部分圆台的下底面半径为：

$R=\left(h_1+h\right)\tan 9^{\circ }$ (15)

然后分别计算每个区间段的气体体积 $V_t$，以及针阀的体积 $V_z$，H为针阀高度，便可以得出如下函数：

$V=V_t+\text{d}{V}_z$ (16)

考虑一个周期 $t=\left[0,100\right]$ 这个时间段，将其分为四个区间，分别为： $\left[0,0.44\right],\left[0.45,2\right],\left[2.01,2.45\right],\left[2.46,100\right]$ 将每一个时间段的总体积V表示出来：

$\{\begin{array}{l}\text{d}{V}_z=\pi R^2\text{d}H\\ V_t=\frac{1}{3}\pi h\left(R^2+r^2+Rr\right)\end{array}$ (17)

所以，在一个周期内，可以得出其转动次数n，有了转动次数，就可以求出柱塞转一圈所需的时间，进而算出角速度，则有：

$\omega =\frac{2\pi \ast M_{in}}{T\ast \rho \text{d}v}$ (18)

(四) 高压油管恒压多喷油嘴柱塞运动模型

当多个喷油嘴工作时，同样的时间内，释压量翻倍，质量变为原来的两倍，必须加快柱塞的转动次数方能达到平衡。由气体质量的守恒得：

$M_{in}+m_{old}=m_{out}+m_{now}$ (19)

由 $m_{old}=m_{now}$， $m_{out}=\rho \text{d}v$ 应有：

$\omega =\frac{2\pi \ast M_{in}}{T\ast \rho \text{d}v}$ (20)

3. 模型检验

(一) 高压油管压力控制模型检验

本文通过微分方程的数值解法和利用MATLAB软件模拟仿真分别对本文模型进行有效性和精确性的检验。根据2019高教社杯全国大学生数学建模竞赛A题的数据 [16]，对所给出的弹性模量与压力关系变化数据进行模拟仿真，得到如图2所示：

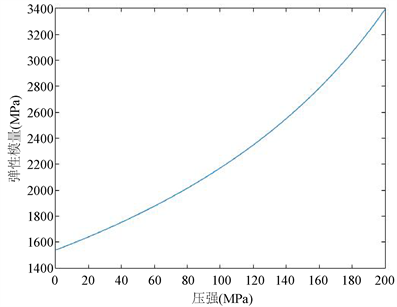
Figure 2. Curve of elastic modulus as a function of pressure

图2. 弹性模量随压强变化的曲线图

通过图像可以得知，趋势是一个递增指数型函数，进一步验证了本文所建立的弹性模量与压力模型 $E\left(p\right)=k{\text{e}}^{\lambda p}$ 的模型的有效性和准确性。做出拟合图像和原图对比，得到的图像效果如图3所示：

Figure 3. Comparison of function fitting and original image

图3. 函数拟合与原图像的对比图

从图中的拟合效果来看，拟合函数图像和原始数据图像几乎重合，所以 $E\left(p\right)$ 函数的表达式可以确定为一个指数型函数，对其进行非线性函数的拟合，得到模型中的 $k=1476.3877$， $\lambda =0.00401$，所以

$E\left(p\right)=1476.3877{\text{e}}^{0.00401p}$

通过对高压油管恒定压力的微分模型的求解，利用计算机模拟仿真画出模型所得到的压强P和时间t的图像，如图4所示：

由图可知，本文选择压强为105 MPa的上限波动最大值，图中的时间是1 s内的开启时间，换算成100 ms的周期，此时的时间为0.64 ms。即每100 ms内开启0.64 ms，压强的增加值为0.5 MPa。

(二) 高压油管恒压喷油嘴柱塞运动模型检验

对所给出的针阀运动曲线数据进行模拟仿真，得到针阀升值随时间的变化曲线如图5所示：

Figure 4. Pressure vs. time image

图4. 压强随时间变化图像

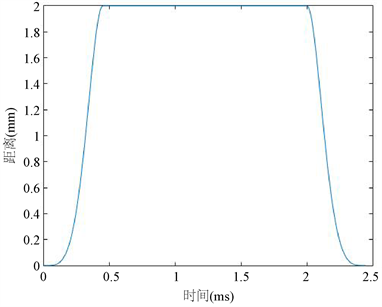
Figure 5. Needle valve rise value with time curve

图5. 针阀升值随时间的变化曲线

由图5可见，针阀开启和关闭两个过程是相互对称的，为一个分段函数，通过对一个周期时间的划分，经过MATLAB数据拟合仿真得到针阀开启时升程高度变化曲线如下图所示：

由图6可知，原始数据曲线和针阀运动升程高度模型拟合曲线完全重合。针阀运动升程高度模型拟合的效果非常好，进一步验证了针阀运动升程高度模型，对其进行非线性函数的拟合，得到模型中的 $a=-772.3439$ 、 $b=570.2069$ 、 $c=-96.5000$ 、 $d=8.8246$ 、 $e=-0.2908$ 、 $\epsilon =0.0017$。所以针阀运动升程高度模型为：

$h\left(t\right)=-772.3439t^5+570.2069t^4-96.5t^3+8.8246t^2-0.2908t+0.0017$

Figure 6. Fit curve of lift height change when the needle valve is opened

图6. 针阀开启时升程高度变化拟合曲线图

综上所述，通过利用现有数据对模型进行检验，进一步说明了本文所建立基于质量守恒的高压油管压力微分模型具有较高准确性、有效性。

4. 结果分析

(一) 高压油管恒压压力控制模型求解结果

针对2019高教社杯全国大学生数学建模竞赛A题的数据 [16]，通过对基于质量守恒的高压油管压力微分模型的求解，并利用计算机模拟仿真，画出模型所得到的只含有压强P和时间t的关系图像，如图7所示：

Figure 7. Pressure vs. time image

图7. 压强随时间变化图像

由图可知，本文选择压强为105 MPa的上限波动最大值，图中的时间是1 s内的开启时间，换算成100 ms的周期，此时的时间为0.64 ms。即每100 ms内开启0.64 ms，压强的增加值为0.5 MPa。

(二) 高压油管不恒压压力控制模型求解结果

通过对高压油管不恒定压力的微分模型的求解，分别得到2 s、5 s、10 s的压强与时间的对应关系。分别如下图8、图9、图10所示：

Figure 8. 0 - 2 second pressure versus time curve

图8. 0~2秒压强随时间的变化曲线

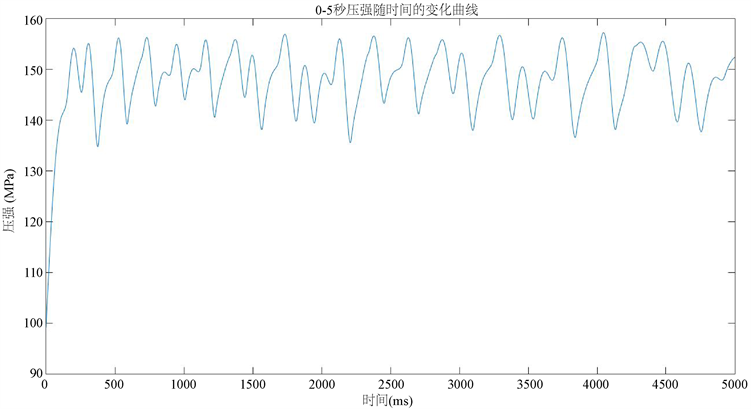
Figure 9. 0 - 5 seconds pressure versus time curve

图9. 0~5秒压强随时间的变化曲线

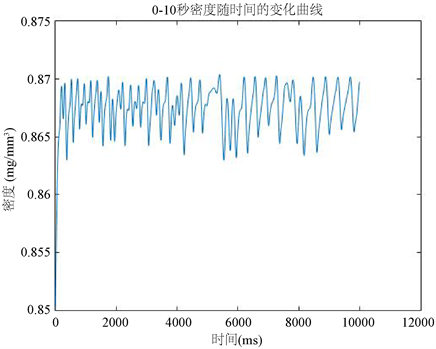
Figure 10. 0 - 10 seconds pressure versus time curve

图10. 0~10秒压强随时间的变化曲线

三个时间段下m-t，ρ-t，P-t关系的图像汇总如图11所示：

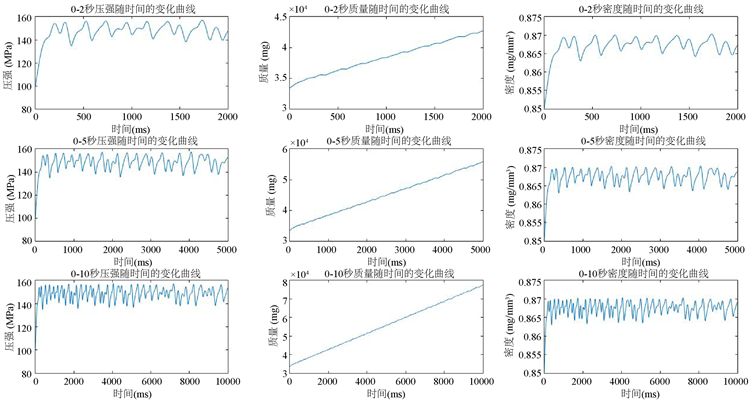
Figure 11. Segmentation curve of three variables with time t

图11. 三个变量随时间t的分段变化曲线

根据三种时间段下，压强和时间的关系曲线，分别找出数据集中所有的开启时间段以及关闭时间段并求和取平均。得到的高压油管油泵和喷油嘴的开关策略为如下表1所示：

由图像和表中数据可知，在0~2 s的调整期内，喷油嘴在一个喷油周期内开启时长为148.0 ms，关闭时间为63.5 ms。在0~5 s的调整期内，喷油嘴在一个喷油周期内开启时长为146.5 ms，关闭时间为62.0 ms。在0~10 s的调整期内，喷油嘴在一个喷油周期内开启时长为148.0 ms，关闭时间为 61.0 ms。

Table 1. Switching strategy table for high pressure tubing oil pump and injector

表1. 高压油管油泵和喷油嘴的开关策略表

(三) 高压油管恒压单喷油嘴柱塞运动模型求解结果

通过对高压油管恒定压力下单喷油嘴柱塞运动模型的求解，计算出公式中需要的常数量： $R=1.25\text{mm}$，

$r=0.7\text{mm}$， $h_1=\frac{r}{\tan 9^{\circ }}=4.4192\text{mm}$ 常数量代入模型中，得道各个m的质量：

$\{\begin{array}{l}{m}_1={132.3578}_1,t=\left[0,0.44\right]\\ m_2=1293.4526,t=\left[0.45,2\right]\\ m_3=12.5873,t=\left[2.01,2.45\right]\\ m_4=0,t=\left[2.46,100\right]\end{array}$

则有： $n=\frac{m_1+m_2+m_3+m_4}{m_{in}}=1.074$， $t_z=\frac{T}{n}=2.2812\text{ms}$， $\omega =\frac{2\pi }{t_z}=2.7543\text{rad}/\text{ms}$。

当高压油管单喷油嘴柱塞在恒定压力下运动时，在一个喷油周期内，高压油管喷油嘴喷油一次，相当于凸轮柱塞转动1.074次，高压油泵凸轮柱塞每转动一圈用时2.2812 ms。高压油泵凸轮柱塞转动的角速度为2.7543 rad/ms。

(四) 高压油管恒压多喷油嘴柱塞运动模型求解结果

通过对高压油管恒定压力下多喷油嘴柱塞运动模型的求解，计算出公式中需要的常数量： $R=1.25\text{mm}$，

$r=0.7\text{mm}$， $h_1=\frac{r}{\tan 9^{\circ }}=4.4192\text{mm}$ 代入上面公式中，计算出各个m的质量：

$\{\begin{array}{l}{m}_1={132.3578}_1,t=\left[0,0.44\right]\\ m_2=1293.4526,t=\left[0.45,2\right]\\ m_3=12.5873,t=\left[2.01,2.45\right]\\ m_4=0,t=\left[2.46,100\right]\end{array}$

分为两种情况进行讨论：

(1) 多个喷油嘴同时开关，则：

$n=\frac{2\left(m_1+m_2+m_3+m_4\right)}{m_{in}}=2.148$

$t_z=\frac{T}{n}=1.1406\text{ms}$

$\omega =\frac{2\pi }{t_z}=5.5086\text{rad}/\text{ms}$

(2) 多个喷油嘴不同时工作，则：

$n=\frac{m_1+m_2+m_3+m_4}{m_{in}}=1.074$

$t_z=\frac{T}{2n}=1.1406\text{ms}$

$\omega =\frac{2\pi }{t_z}=1.37715\text{rad}/\text{ms}$

当高压油管多个喷油嘴柱塞在恒定压力下运动，多个喷油嘴同时开关时，在一个喷油周期内，高压油管喷油嘴喷油一次，相当于凸轮柱塞就转动2.148次，高压油泵凸轮柱塞每转动一圈用时1.1406 ms。高压油泵凸轮柱塞转动的角速度为5.5086 rad/ms。多个喷油嘴不同时工作时，在一个喷油周期内，高压油管喷油嘴喷油一次，高压油泵凸轮柱塞就转动1.074次，高压油泵凸轮柱塞每转动一圈用时1.1406 ms。高压油泵凸轮柱塞转动的角速度为1.37715 rad/ms。

5. 总结

本文通过所建立的基于质量守恒方程的高压油管压力控制模型对2019高教社杯全国大学生数学建模竞赛A题数据 [16] 处理，并对其进行结果分析，总结如下：

1) 本文通过建立的基于质量守恒方程的高压油管压力控制模型进而推导得到压强与时间、压强与密度的数学模型，在质量守恒的条件下，通过计算机模拟仿真可以直观的得到压强与时间、压强与密度的关系和变化规律。

2) 燃油进入和喷入高压油管是燃油机的工作原理，研究燃油机的高压油管压力控制意义深刻，本文通过对燃油机高压油管压力控制研究后，解决了高压油管压力控制方面的问题，得出了高压油管的压力控制相关方案。

3) 在分析高压油管工作原理和燃油压力关系的基础上，本研究运用微分方程建立了基于质量守恒方程的高压油管压力控制模型对压力变化进行模拟仿真，并获得了较为理想的仿真结果结果。在今后可将此模型用于压力变化的问题之中。

基金项目

西南科技大学大学生创新基金项目(项目编号：CX19-061)。