1. 引言
本文中所考虑的图都是连通的,无向的,无自环且无重边的。对于一个图
,我们用
,
和
分别表示其顶点集,弧集和全自同构群。
表示图
的阶(即
顶点的个数)。如果
的一个子群G作用在
(
)是传递的,则称
是G-点传递的(G-弧传递的)。一个弧传递图也称为对称图。对一个正整数s,
中
个点
满足
与
(
)邻接且
(
),我们称
为
的一条s-弧。如果
在s-弧集上是传递的,则称
是
-弧传递的。进一步,如果
在s-弧集上传递,在
-弧集上不传递,那么
叫作
-传递。
对阶数固定的对称图的研究一直是代数图论领域一个很热门的课题,例如,文献( [1] [2] [3] )分别分类了阶为p,2p和3p的对称图。对于一些小度数的图也有很多学者研究,更多文献可参考( [4] - [9] )。1947年,Tutte在文献( [10] )中给出了3度图的点稳定子结构。此后,3度对称图得到了很多学者的关注,例如:Feng等在文献( [4] )中刻画了两倍素数幂的3度对称图;Lu等在文献( [8] )中研究了阶为6p2的3度对称图;Zhou和Feng在( [11] )中分类了2pq阶的3度对称图。
设
是一个传递置换群,如果G的每个极小正规子群在
上都是传递的,则称G是拟本原的;如果G的每个极小正规子群在
上至多有两个轨道且存在一个极小正规子群在
上恰好有两个轨道,则称G是二部拟本原的。对于一个图
,
,如果G在顶点集
上是拟本原或二部拟本原的,则称
是一个G-基图。研究对称图的方法分为以下两步:
第一步,刻画基对称图;
第二步,研究基图的正规覆盖。
上述步骤我们可以看出对基图的刻画是研究对称图的基础,它对作基图的覆盖具有重要的参考作用。设
是阶为
(
)的3度G-弧传递图,本文中我们刻画
的基图,其中p,q为素数且
, 。主要结论如下:
。主要结论如下:
定理1.1 设
是阶为
( )的3度G-弧传递图,其中p,q为素数且
,设
在
上是拟本原或二部拟本原的,
,则
满足表1。
)的3度G-弧传递图,其中p,q为素数且
,设
在
上是拟本原或二部拟本原的,
,则
满足表1。

Table 1. G-basic symmetric graphs of order 4 p q n and valency 3
表1.
阶3度G-基对称图
关于本文中所使用的群论和图论的相关符号都是标准的,可参考文献( [12] [13] [14] )。例如:我们用 ,
和
分别表示n阶循环群,交错群和对称群。对于一个单群T,我们用
表示
的素因子集合。
,
和
分别表示n阶循环群,交错群和对称群。对于一个单群T,我们用
表示
的素因子集合。
2. 预备知识
在本节中,我们给出一些与本文相关的定理和例子。首先是Tutte在1947年确定的3度对称图的点稳定子的结构,它是我们研究3度图的基础。
定理2.1 ( [10] ) 设
是一个连通的3度
-弧传递图,则
,则
满足表2,其中
。

Table 2. Point-stabilizer groups of cubic symmetric groups
表2. 3度对称图的点稳定子
对于一个图
,如果点稳定子
在
的邻域
上是本原的,则称
为局部本原的,由于素
数度的弧传递图是局部本原的,因此下面的结论( [15],引理2.5)提供了研究局部本原图的基本方法,这个结论对Praeger的结果( [16],定理4.1)进行了改进。
定理2.2 ( [15] ) 设
是一个连通的奇素数度的G-弧传递图,
有一个非传递正规子群N在
上至少有三个轨道。则下列事实之一成立:
1) N在
上半正则,
,
是
-弧传递的且
是
的正规N-覆盖;
2)
是
-弧传递的当且仅当
-弧传递的,其中
或
;
3)
,其中
,
。
在文献( [16] )中,Praeger将拟本原置换群分为八类,我们将其称为O’Nan-Scott-praeger定理。下面我们简述O’Nan-Scott-praeger定理。
定理2.3 ( [16] )拟本原置换群可以分为以下八类:
HA (仿射型):
是交换的, ,其中p是素数,
,其中p是素数, 。
。
HS (全形单型): ,其中
。
,其中
。
HC (复合全型):
,其中
。
AS (几乎单型):
是非交换单群,
。
TW (扭圈积型): 在
上正则,
,其中
。
在
上正则,
,其中
。
SD (单对角型):
,
,
,其中
,
。
CD (复合对角型):
,
,
,其中 ,
,
。
,
,
。
PA (乘积作用型):
,
,其中 ,
。
,
。
对于以下较小的群G,我们可以利用Magma ( [17] )确定所有同构意义下的弧传递图,并且得到下面的几个例子。
例2.4 (1)
,则G存在子群同构于
,此时存在一个阶为220阶的3度对称图,记为
。 。
。
(2)
,则G存在子群同构于
,此时存在一个阶为220阶的3度对称图,记为 。
。
。
。
例2.5 (1)
,则G存在子群同构于
,此时存在一个阶为364阶的3度对称图,记为
。
。
(2)
,则G存在子群同构于
,此时存在一个阶为364阶的3度对称图,记为
。
。
例2.6
,则G存在子群同构于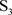 ,此时存在一个阶为1012阶的3度对称图,记为
。
。
,此时存在一个阶为1012阶的3度对称图,记为
。
。
例2.7
,则G存在子群同构于
,此时存在一个阶为4324阶的3度对称图,记为
。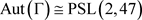 。
。
3. 定理1.1的证明
本节中,我们分以下三个引理来完成定理1.1的证明。
引理3.1 设T是一个非交换单群,
,且
,其中
为素数。则
,
,
,
,
,
, ,
,
,
,或
。
,
,
,
,或
。
证明:由于有限p-群和
(m,n为素数,a,b为正整数)阶群都可解,而可解单群必为素数阶循环群,所以
或2,因此
或4。如果
,由文献( [12],定理1),T同构于( [12],表1)中的八个群之一,又因为
通过检查群的阶,满足条件的群只有
,
,或
。
假设
。则
且
。由此可知
。 (1)
由文献( [12],定理1),T同构于( [12],表3)中的某个群或
,其中q是一个素数幂。对于前一种情况,由于
,由( [12],表3)查得不存在满足条件的群。
如果
,则有
且
,因此
,其中
且
。如果
,由式子(1)和
可知,
或25,即
,或
,如果
,此时有
,
即
。
我们注意到
,于是
或
,因此q = 11,13,23,31,47,49,97或193。通过检查群的阶可得,
,
,
,
,
或 。
。
之后,我们总假设
是一个阶为
(
)的连通G-弧传递3度图,且G在
上是拟本原或二部拟本原的,其中
。令
。
引理3.2 假设G在
上是拟本原的,则
,
,
,
,
或
。
证明:设N是G的一个极小正规子群。则N为同构单群的直积,即
,其中
(
)是一个单群。因为G在
上拟本原,所以N在
上是传递的。如果N是交换的,则N在
上半正则,于是
,这是不可能的,故N是非交换的。首先我们断言
。事实上,由
的连通性及 ,我们可知
是N-弧传递的。此时,如果
在
上传递,由( [14],定理4.2A)可知
的中心化子
(即
)是半正则的,与
矛盾。如果
,我们可知
是N-弧传递的。此时,如果
在
上传递,由( [14],定理4.2A)可知
的中心化子
(即
)是半正则的,与
矛盾。如果 在
上至少有三个轨道,则由定理2.2可知
是半正则的,同样是一个矛盾。从而
在
上恰好有两个轨道U和W。又因为
,因此U和W构成
上一个N-不变划分,这就意味着集合稳定子
在N中的指数为2,而
中没有指数为2子群,矛盾。于是
。
在
上至少有三个轨道,则由定理2.2可知
是半正则的,同样是一个矛盾。从而
在
上恰好有两个轨道U和W。又因为
,因此U和W构成
上一个N-不变划分,这就意味着集合稳定子
在N中的指数为2,而
中没有指数为2子群,矛盾。于是
。
因此
是T-弧传递的,故
满足定理2.1。于是由T的传递性可以得到,
。又因为
是T-弧传递的,故
,从而
,即T满足引理3.1。
假设 ,则T和
,则T和 如表3所示。
如表3所示。

Table 3. Nonabelian groups with 3 prime factors and ( p , q n )
表3. 含有3个素因子的单群及对应
取值
如果
,则
,即
。由Magma ( [17] )计算可得,满足条件的图 不存在。如果
,则
,即
。由文献( [18] )可知
,如果
,则
,即
。但是
中没有子群同构于
,这是不可能的。
不存在。如果
,则
,即
。由文献( [18] )可知
,如果
,则
,即
。但是
中没有子群同构于
,这是不可能的。
假设
,则T和
如表4所示。

Table 4. Nonabelian groups with 4 prime factors and ( p , q n )
表4. 含有4个素因子的单群及对应
取值
如果
,则
,即
,由例2.4可知
。如果
,则
,即
。由例2.5可知
。如果
,则
,即
,但
中没有同构于
的12阶子群。如果 ,则
,即
,则
,即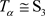 ,由例2.6可知
。如果
,则
,即
,由文献( [18] )可知
。同样地,由例2.7可以得到
,此时
,
。而对于
和
,有
和
,但是对应的T都没有子群同构于
,由例2.6可知
。如果
,则
,即
,由文献( [18] )可知
。同样地,由例2.7可以得到
,此时
,
。而对于
和
,有
和
,但是对应的T都没有子群同构于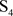 和
。
和
。
引理3.3 G在
上是二部拟本原的,则
,或
。
证明:因为G在
上二部拟本原,所以G存在极小正规子群
在
上恰好有两个轨道
和
,那么
就是一个二部图。令
,则有
,
且
。假设
作用在
上是不忠实的,由( [19],引理5.2),是一个完全二部图,又因为
为3度图,则
,即
,与
矛盾。从而
作用在
(
)上忠实,由( [20],定理1.5)可知,下述之一成立:
1)
在
上是拟本原的;或
2)
中存在两个正规子群
和 ,使得
且在
上半正则。进一步地,有群
在
上是正则的。
,使得
且在
上半正则。进一步地,有群
在
上是正则的。
对于(2),我们可以得到
,这是不可能的。
故(1)成立,因为
,由定理2.3可知,
是几乎单或乘积作用型。设
是
的基柱。其中T是非交换单群且 。
。
假设
是几乎单的,因此
。进一步地,如果T不是G唯一的极小正规子群,由于
,我们很容易可以得到
,也就是说G有正规子群
在
上有
个轨道,与G的二部拟本原性矛盾。从而G是几乎单的,设
。因此我们可以令
,
,其中 且
。
且
。
因为
,由定理2.1可知
,因此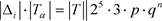 。另一方面,由于
,我们可以得到
。另一方面,由于
,我们可以得到 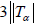 ,从而
,故T满足引理3.1且
或4。
,从而
,故T满足引理3.1且
或4。
当
时,则T和
满足表3。如果 ,则
。因为
,所以
,
或
,
。故
或 ,
或
。由Magma ( [17] ),这两种情况下都没有图
,则
。因为
,所以
,
或
,
。故
或 ,
或
。由Magma ( [17] ),这两种情况下都没有图 存在。如果
,因为
没有指数为2的子群,与
矛盾。如果
,因为
,
,所以
,
,由Magma ( [17] ),不存在满足条件的图
。
存在。如果
,因为
没有指数为2的子群,与
矛盾。如果
,因为
,
,所以
,
,由Magma ( [17] ),不存在满足条件的图
。
当
时,
满足表4。如果
,则
,从而 。这与定理2.1矛盾。如果
,则
,因为
,矛盾。如果
,则
。因为
。这与定理2.1矛盾。如果
,则
,因为
,矛盾。如果
,则
。因为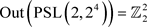 ,故
或
,且对应的
分别为
,故
或
,且对应的
分别为 或
,由Magma ( [17] )可知
中没有24阶子群,
或
,由Magma ( [17] )可知
中没有24阶子群, 中没有同构于
的48阶子群,矛盾。如果
,则
。又因为
,所以
且
中没有同构于
的48阶子群,矛盾。如果
,则
。又因为
,所以
且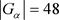 。与
中没有48阶子群矛盾。若
或
。与
中没有48阶子群矛盾。若
或 时,由Magma ( [17] ),不存在这样的3度对称图。若
或
,由例2.4和2.5可知,
或
。
时,由Magma ( [17] ),不存在这样的3度对称图。若
或
,由例2.4和2.5可知,
或
。
假设
是乘积作用型的,则
,其中 (
)是一个单群。如果
(
)是一个单群。如果 在
在 上是传递的,由( [14],定理4.2A)可知
是半正则的,故
,矛盾。从而
在
和
上是传递的,由( [14],定理4.2A)可知
是半正则的,故
,矛盾。从而
在
和 上都不传递,由( [8],引理3.2)可知
是半正则的,同样可以推出矛盾。
上都不传递,由( [8],引理3.2)可知
是半正则的,同样可以推出矛盾。
基金项目
国家自然科学基金资助项目(80031010061)资助。