电磁辐射背景下的神经动力学研究

Study on the Neural Dynamics under the Effect of Electromagnetic Radiation

摘要: 长期暴露在低频磁场下可能导致神经性疾病，本文基于考虑电磁辐射的Hindmarsh-Rose神经元模型，对电磁辐射背景下的神经发放行为进行了研究。电磁辐射作用效果支撑了包含单周期、多周期、复杂周期等多种神经发放模式。在传统的神经模型分岔分析中，外部刺激电流是决定神经发放模式的关键因素。我们的研究结果表明电磁作用效果与外部刺激电流共同决定神经发放模式，改变电磁作用效果能诱导神经发放模式转迁。这将有助于从理论上理解电磁作用效果在神经动力学行为中所起到的关键性作用。为预防和治疗电磁辐射相关的神经疾病提供理论启发。

Abstract: Long-term exposure to low-frequency magnetic fields may lead to neurological diseases. Based on the Hindmarsh-Rose neuron model considering electromagnetic radiation, the neuronal firing be-havior under the background of electromagnetic radiation was studied. The effects of electromag-netic radiation support a variety of nerve delivery modes including single periodic, multi-periodic and complex-periodic patterns. In the traditional bifurcation analysis of neural models, the external stimulus current is the key factor to determine the mode of neuronal firing. Our results show that the effect of electromagnetic interaction and external stimulus currents together determine the mode of neuronal firing. Changing the effect of electromagnetic interaction can induce the mode transition of neuronal firing. This will help us to understand theoretically the key role of electro-magnetic effects in neural dynamical behavior, and provide theoretical inspiration for the preven-tion and treatment of neurological diseases related to electromagnetic radiation.

1. 引言

神经系统是生物体内起主导作用的功能调节系统。生物体内各器官、系统的功能和各种生理过程是在神经系统的调控下实现和维持正常的生命活动。在理论研究中，针对不同的细胞类型、实验或出于不同的理论研究需要提出了不同的数学模型来描述神经电活动 [1]。例如，Hodgkin-Huxley (HH)模型、Morris-Lecar (ML)模型、FitzHugh-Nagumo (FHN)模型、Hindmarsh-Rose (HR)模型、Integrate-and-Fire (IF)模型等等 [2] - [11]。

人类生活在不同频率和强度的电磁场背景下，这使得研究电磁场背景下的神经动力学成为有现实意义的理论课题。大量证据表明，电磁场环境下的神经元存在多种不同的生物学响应。例如应用于皮肤瘤治疗的电穿孔现象 [12]；经颅磁刺激用于癫痫 [13]、帕金森病 [14] 的治疗；电磁场控制神经突触可塑性 [15]、神经元可激发性 [16] 等。1996年，世界卫生组织发起了电磁场相关联的健康问题研究 [17]。研究表明，超低频磁场(1-100KHZ)是一种可能的致癌物，尤其是脑肿瘤 [18]。长期暴露在低频磁场下可能导致老年痴呆、综合性运动神经疾病、肌肉萎缩侧索硬化、阿尔茨海默病等 [19] [20]，但其致病机理尚不清楚。一些相关的实验工作发现低频磁场能诱导模式生物中枢神经系统生化反应异常，能提高初期神经干细胞的增殖 [21]。

理论上一般认为，电磁场诱导的神经响应主要来源于电磁场改变神经元的跨膜电压。在单细胞层次，Schwan最早导出了低频场造成的跨膜电压改变公式 $\Delta V=1.5E0Rcos\theta$ (E0为外场强度，R为细胞半径，θ为膜法向与场方向的夹角) [22]，Zheng Yu等采用Hodgkin-Huxley神经模型，基于能斯特–普朗克方程推导了一个电磁场神经模型，该模型能计算神经跨膜电压和离子电流 [23]。马军等 [24] [25] [26] [27] 基于电磁感应定律，引入“磁通”变量来对神经元复杂电活动进行建模，模型将来自于细胞内外的电磁辐射考虑为背景噪声，研究了不同噪声强度下的神经发放模式，而对于该模型的确定性动力学缺乏细致的探讨。

本文将对马军等提出模型的确定性版本，进行详细的分岔分析，再现模型所支撑的丰富的神经发放模式，从而探讨电磁辐射在决定神经发放模式中所起到的关键性作用，并揭示其非线性动力学机制。这从理论上能更进一步认识该模型，拓展其应用场景，并将有助于从理论上揭示和解释电场致病的生物机理，为预防和治疗此类疾病提供理论依据。

2. 模型和计算设定

该模型采用改进型的Hindmarsh-Rose(HR) [5] 神经元模型来模拟神经动力学，并增加了一个磁通变量来模拟电磁作用效果，确定性模型方程可以写成 [24] [25] [26] [27]

$\stackrel{\dot{}}{x}=y-a{x}^3+b{x}^2-z+I_{ext}-k_{1}W\left(\phi \right)x$

$\stackrel{\dot{}}{y}=c-d{x}_2-y$

$\stackrel{\dot{}}{Z}=r\left[S\left(X+1.6\right)-Z\right]$

$\stackrel{\dot{}}{\phi }=kx-k_2\phi$ (1)

其中x代表神经元细胞膜的电位；y代表与内电流相关的恢复变量；z代表与钙离子激活的钾离子电流相关的慢变调节电流； $\phi$ 代表通过神经元膜上的磁通量； $k_{1}W\left(\phi \right)x$ 表示磁通量变化时的反馈电流； $k_1$ 是反馈增益系数，可以表示电磁辐射的作用强度，是本文进行分析讨论的重要分岔参数；a，b，c，d，r和s为四维神经元模型参数； $kx$ 和 $k_2\phi$ 分别表示薄膜电势对磁体磁通和漏磁的影响通量； $I_{ext}$ 为外部刺激电流。对于单神经模型而言， $I_{ext}$ 包含了神经元所接收到的突触电流，或者刺激素对特定膜蛋白绑定所触发的离子交换等。神经突触可能是抑制性或者兴奋性，分别对应于 $I_{ext}$ 取正值和负值。此外，在模型中，

$W\left(\phi \right)\text{=}\frac{\text{d}q\left(\phi \right)}{\text{d}\phi }=\alpha +3\beta {\phi }^2$ (2)

$\left(\phi \right)x$ 的物理意义可以通过下面的式子来描述：

$i=\frac{\text{d}q\left(\phi \right)}{\text{d}t}=\frac{\text{d}q\left(\phi \right)}{\text{d}\phi }\frac{\text{d}\phi }{\text{d}t}=W\left(\phi \right)\frac{\text{d}\phi }{\text{d}t}=W\left(\phi \right)V=k_{1}W\left(\phi \right)x$

其中V为电动势，且物理单位与电动势相同， $\alpha$， $\beta$ 也是表示模型参数，本文的固定参数a = 1.0，b = 3.0，c = 1.0，d = 5.0，r = 0.006，s = 4，k = 0.9， $k_2=0.5$， $\alpha =0.1$， $\beta =0.02$。如前所述，反馈增益系数 $k_1$ 表示电磁辐射的作用强度，将作为主要分叉参数；另外，在很多神经模型的分岔分析中都将 $I_{ext}$ 作为分岔参数，本文也将 作为另外一个分岔参数。数值模型采用经典的四阶Runge-Kutta法对神经元模型进行数值求解，时间步长取0.001时间单位，大量的计算表明，更小的步长不会进一步改变计算结果。另外，在不同的参数条件下，系统需要不同的时间收敛到稳定的动力学发放。我们的数值模拟发现在2000时间单位后，系统都能收敛到稳定的状态。因此，所有的时间演化都经过2000时间步长的消除暂态过程。

Figure 1. Firing pattern for I_ext = 3.6, k₁ = −0.15. (a) Time-evolution of membrane potential x; (b) Phase diagram for variable x and y in the model; (c) Phase diagram for variable x and z in the model

图1. 当参数值I_ext = 3.6, k₁ = −0.15时的神经发放模式。(a) 神经元膜电位x随时间演化图；(b) 模型中，x, y两个变量在神经动力学过程中的相图；(c) 模型中，x, z两个变量在神经动力学过程中的相图

3. 结果与讨论

如前所述，本文主要通过分岔分析来讨论电磁辐射效应的存在对神经发放的影响。所以下面我们首先将 $I_{ext}$ 固定在一个典型的值3.6，改变参数k₁来模拟不同程度的电磁作用对神经元动力学的影响。图1显示了 $k_1=-0.15$ 时的神经发放斑图。从图1(a)可以看出神经元呈现出单周期的发放，发放周期约为28.3时间单位。图1(b)和图1(c)相图中的闭合极限环(Limit cycle)进一步应证了这种单周期发放。

为了更进一步显示考虑电磁效应对神经元动力学的影响，图2展示了 $k_1=-1.4$ 时的神经动力学行为。从图2(a)中可以看出神经元呈现出周期性Bursting式的发放。其Bursting周期约为245.4时间单位，在一个Bursting周期内约发生16次Spike，这一数目对k₁的依赖关系有待进一步研究。另外在一个Bursting周期内，Spike峰间距(Inter-Spike Interval)发生逐次的变化，变化范围约为5~14时间单位。从非线性动力学的角度来看，神经元的行为是一种多周期振荡行为，图2(b)和图2(c)的相图更清晰地展现了这种多周期行为。

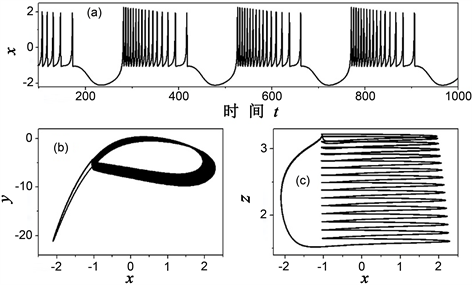
Figure 2. Firing pattern for I_ext = 3.6, k₁ = −1.4. (a) Time-evolution of membrane potential x; (b) Phase diagram for variable x and y in the model; (c) Phase diagram for variable x and z in the model

图2. 当参数值I_ext = 3.6, k₁ = −1.4时的神经发放模式。(a) 神经元膜电位x随时间演化图；(b) 模型中，x, y两个变量在神经动力学过程中的相图；(c) 模型中，x, z两个变量在神经动力学过程中的相图

Figure 3. Firing pattern for I_ext = 3.6, k₁ = −1.08. (a) Time-evolution of membrane potential x; (b) Phase diagram for variable x and y in the model; (c) Phase diagram for variable x and z in the model

图3. 当参数值I_ext = 3.6, k₁ = −1.08时的神经发放模式。(a) 神经元膜电位x随时间演化图；(b) 模型中，x, y两个变量在神经动力学过程中的相图；(c) 模型中，x, z两个变量在神经动力学过程中的相图

图3展示了 $k_1=-1.08$ 时的神经动力学行为。从图3(a)中可以看出神经元的发放呈现出混合模式，其中既包含Bursting式的发放，也包含了简单周期发放的成分。两种发放模式的出现显示出了一定的随机性。从非线性动力学的角度，这种随机混合神经发放模式可以称之为复杂周期振荡行为。图3(b)和图3(c)中的相图也更清晰的反应了神经发放的非周期性和随机性。

为了全面展示电磁辐射效应对神经动力学的影响，我们系统地改变两个参数I_ext和k₁来研究神经发放模式，计算结果展示在图4中。图中白色参数区域神经元不发生发放行为；图中浅灰色参数区域，神经元发生简单周期发放(如图1)；深灰色区域神经元发生Bursting式的多周期发放(如图2)；而网格参数区域内，神经元系统发生随机混合式的神经发放(如图3)。图1~4所展示的各种神经发放模式是几种常见的神经行为。例如，实验研究报道，豚鼠下橄榄神经元的发放呈现出很好的规则行为；猫丘脑网状神经元的发放就呈现了图2所展示的多周期Bursting行为；而在特定的实验条件下，猫丘脑网状神经元又会展现出图3所示的非规则行为 [28]。

Figure 4. The parameter regions for different firing patterns, where the white region represents resting states. Figures 1-3 are obtained for I_ext = 3.6, which is indicated by the dashed line

图4. 不同神经发放模式的参数范围，图中空白区域表示无神经发放。虚线标识出I_ext = 3.6，图1~3的参数取值位于该虚线上的不同区域

可以看出，只有当I_ext > 0是神经元才可能发生发放行为，在I_ext < 0的条件下，任何程度的电磁作用效果都不能产生神经发放行为，因此神经元发放主要是由外部刺激电流来诱导。在I_ext > 0的参数范围内，一定程度的电磁作用效果能诱导神经发放模式的改变。过强的正向或反向电磁作用能彻底抑制神经发放行为，如图所示，只有在−8.2 < k₁ < 5.7的范围内，申请发放才可能被外部刺激电流维持，区域外的强电磁作用可以抑制掉任何刺激电流所激励的神经发放。另外我们可以看到图4中网格参数区域非常小，而且介于多周期和单周期参数范围之间。因此，网格区域所标示的随机混合发放模式可以看成是单周期和多周期两种发放模式之间转迁的过度态。从图中可以看出，这种发放模式的转迁既可以通过外部刺激电流I_ext的变化来诱导，也可以通过k₁的变化来诱导。

为了更进一步地阐明参数变化对神经发放模式的影响，我们计算了神经发放的Spike峰间距(ISI)。其中，图5的中间图给出的是当I_ext = 3.6时，不同k₁取值对应的ISI。I_ext = 3.6的参数值在图4中用红色虚线标识。对照图5和图4可以看出，图4中ISI在−0.58 < k₁ < 0.70范围内的单一取值对应于图5中的虚线穿越的周期发放区域。而在k₁ < −1.33和k₁ > 1.10区域内，ISI明显分裂为差异很大的两支，之中较大的一支对应于图2中显示的Bursting周期，而较小的分支对应于Spike尖峰周期。另外，图4中−1.33 < k₁ < −0.58和0.70 < k₁ < 1.10的参数范围内，ISI的取值呈现出的多样性正好对应于图5中红虚线穿越的复杂周期区域。

Figure 5. The dependence of Inter-spike intervals(ISI) on the parameter k₁for different firing patterns

图5. 不同参数取值的神经发放模式中，峰间距(ISI)随着参数k₁的变化情况

另外图5(a)给出的是I_ext = 6.0的ISI。单一的ISI取值完美地对应I_ext = 6.0在图4中所处的简单周期发放参数范围；而在图5(c)中的两个分支正好说明I_ext = 2.0在图4中完全落在多周期Bursting发放区域。

在图3深灰色参数区域和图2所示的Bursting式的多周期发放中，一个Bursting周期中往往包含的神经Spike数目也受到外部刺激电流和电磁效应的影响。我们改变参数进行了系统的研究。图6(a)显示，对于给定的外部刺激电流I_ext，Spike数目总是随着k₁的增加而减小；反之，图6(b)显示，对于给定的k₁，Spike数目总是随着外部刺激电流I_ext的增加而增加。比较图6(a)和图6(b)，我们还能得到结论：相比较而言，电磁效应的作用效果比外部刺激电流对Spike数目的影响更大。理论上来讲是因为，电磁作用效果通过复杂的动力学过程来影响神经发放，而外部刺激电流是通过一个固定的电流项来影响神经发放。当然这一结论的正确性需要进一步的实验验证。另外，k₁取值的正负不同，实际上代表着不同方向的电磁作用效果。在这里，我们姑且称之为“正向”和“反向”。从图6(a)可以看出，“反向”电磁作用对Spike数目的影响远大于“正向”电磁作用。

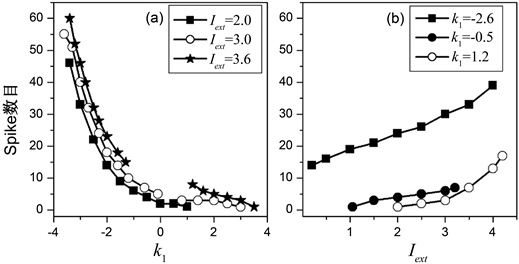
Figure 6. The number of spike in one Bursting period. (a) The number of spike as a function of k₁ for given values of I_ext; (b) The number of spike as a function of I_ext for given values of k₁

图6. 一个Bursting周期中包含的神经Spike数目。(a) 给定的外部刺激电流I_ext下，Spike数目随着k₁的变化；(b) 给定k₁，Spike数目随着外部刺激电流I_ext的变化

4. 总结

随着社会的发展和进步，越来越多的电子产品进入人们的生活，人类生活在一个复杂的电磁环境中。基于一个考虑电磁辐射作用的改进型的HR神经元模型，我们研究了电磁辐射作用效果的存在对神经发放模式的影响。模型再现了多种神经发放模式：单周期发放；Bursting式的多周期发放；混合的复杂周期发放。我们通过改变参数k₁来模拟电磁辐射作用效果。在传统的神经模型分岔分析中，外部刺激电流是决定神经发放模式的关键因素。我们的研究结果表明电磁作用效果与外部刺激电流共同决定神经发放模式，改变电磁作用效果能诱导神经发放模式转迁。在Bursting式的多周期发放中，电磁辐射作用能决定Bursting周期内的包含的发放次数。本研究的结果有助于我们了解在神经动力学建模中认识到电磁辐射作用的重要性，也为外加电磁场来影响神经元的研究提供了理论基础。

NOTES

^*通讯作者。