储能柜冲击试验仿真和随机振动疲劳寿命研究

Research on Impact Test Simulation and Random Vibration Fatigue Life of Energy Storage Cabinet

摘要: 超级电容的优良性能使其在轨道交通车辆的装车占比越来越大，为适应超级电容储能柜结构紧凑和较高的轻量化要求，对柜体结构进行强度仿真和疲劳寿命预估就变得越发复杂和重要。针对某列车储能柜，根据标准IEC 61373-2010，采用有限元分析软件，应用模态叠加法模拟了冲击试验过程中的受力情况，计算了随机振动环境下的响应，得到了结构的1σ、2σ、3σ Von Mises最大应力。利用材料的S/N曲线，并基于高斯分布和Miner提出的线性疲劳累计损伤理论，对结构在给定随机振动环境下的疲劳寿命进行了预估。结果验证了仿真方法的可行性，为产品的安全和可靠性设计提供依据。

Abstract: The excellent performance of super capacitor makes it more and more important to load in rail transit vehicles. In order to adapt to the compact and high lightweight requirements of super ca-pacitor energy storage cabinet, the strength simulation and fatigue life prediction of the cabinet structure become more and more complex and significant. For a train energy storage cabinet, ac-cording to the Standard IEC 61373-2010, the finite element analysis software is used to simulate the stress in the process of impact test by mode superposition method. The response under random vibration environment is calculated, and the maximum Von Mises stress of 1σ, 2σ, 3σ is obtained. Based on the S/N curve of the material, the fatigue life of the structure under the given random vibration environment is estimated based on the Gauss distribution and linear fatigue cumulative damage theory proposed by Miner. The results verify the feasibility of the simulation method and provide the basis for the safety and reliability design of products.

1. 引言

随着列车速度的提高、轴重的增加，对车载设备安全性、可靠性提出了更高的要求。超级电容以循环寿命长、功率密度大、充放电速度快、高低温性能好、容量配置灵活、环境友好免维护等优点 [1]，其装车占比越来越大。然而在进行超级电容储能器柜体结构设计时，要求其结构紧凑及有较高的轻量化水平，因此对储能柜的结构强度与寿命的评估就变得愈来愈复杂和重要。列车储能柜冲击强度与模拟长寿命随机振动疲劳试验是基于ICE 61373-2010标准，通过该试验即认为储能柜满足设计要求。

在储能柜产品设计定型初期，通过仿真分析发现结构设计缺陷，并对结构设计方案进行改进，可避免实物样机试验时出现问题，从而降低开发成本，提高产品开发效率。本文通过基于模态叠加法的瞬态分析法计算储能柜的冲击响应，以及基于随机振动响应下的1σ、2σ、3σ应力计算的振动疲劳寿命，对试验过程中的受力情况进行模拟，从而对试验结果进行评估，提高产品的结构可靠性设计水平 [2] [3]。

2. 冲击试验方法与理论

IEC 61373-2010标准中冲击试验为对设备施加持续时间为D、峰值为A的单个半正弦脉冲加速度，如图1所示，纵向、横向、垂向幅值分别为5 g、3 g和3 g，以验证设备是否满足极限工况的要求 [4]。为了避免共振效应的影响，2次冲击之间应该相隔足够长的时间。设备一共需要在3个方向正反向承受各3次即一共18次的冲击。

冲击分析属于典型的动力学问题。对于多自由度系统，考虑粘性阻尼，其受迫振动的微分方程为 [5] ：

$M\ddot{u}+C\stackrel{\dot{}}{u}+Ku=f\left(t\right)$ (1)

在求解动力学方程(1)时，可以采用直接积分法，也可以采用模态叠加法。模态叠加法是将系统的位移转换到以固有模态为基向量的空间，它对系统本质特性并无影响，通过以求解广义特征值为代价，得到n个非耦合单自由度系统运动方程。模态叠加法求解单自由度系统要比对联立方程组直接求解的方法节省时间。在有限元分析中由于自由度是有限的，其对低阶特征解近似性较好，对于高阶较差，而高阶频率对系统实际影响较小，因此本文针对该类储能柜，将采用模态叠加法进行结构瞬态冲击分析。

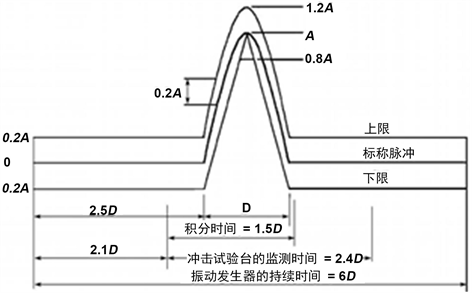
Figure 1. Diagram of half sine pulse of impact test

图1. 冲击试验半正弦脉冲图

3. 随机振动试验及评估方法

由于随机振动的响应是随机的，所以无法用确定的时间函数来描述，但是从统计的角度看，存在一定的规律，可用统计特性进行描述。工程应用中通常使用功率谱密度(Power Spectrum Density, PSD)从频域角度来描述载荷及响应的统计规律 [6] [7] [8]。

ICE 61373-2010标准中规定了不同重量设备在不同安装部位时所采用的PSD试验频谱，用来模拟设备在列车实际运行环境下的振动情况，其中采用长寿命试验量级的振动试验用来模拟设备在25年的使用寿命。在模拟长寿命试验中，标准规定对设备进行纵向、横向、垂向这3个互相垂直的方向分别进行5 h，一共15 h的振动试验，设备通过试验则认为其疲劳寿命可满足使用要求。

随机振动下结构疲劳评估方法主要有时域和频域两种方法，时域法中经典的雨流循环计数方法被认为是最准确的方法，但由于计算量较大，在工程实践中应用受到很大限制 [9]。结合实际试验情况，本文将采用基于频域的谱分析法，通过载荷PSD从频域角度计算出响应的统计规律，再根据Miner提出的线性累积损伤理论和材料S/N曲线，对储能柜结构疲劳寿命进行分析 [10]。该方法为随机振动环境下储能柜结构的随机振动分析和疲劳设计提供了一种有效的计算方法。

在疲劳分析中，Miner线性累积损伤理论由于其形式简单，具备一定的实际理论基础而获得了广泛应用 [11]。Miner线性累积损伤假设从能量的角度出发，认为结构吸收的能量达到极限值时产生破坏。具体从材料S/N曲线上看，在某一应力水平S₁下，对应的破坏时的疲劳寿命为N₁，当实际循环数为n₁时，材料产生的损伤为：

$D_1=n_1/N_1$ (2)

当m个不同的应力水平S_m共同作用时，对损伤进行线性累加，即：

$D={\displaystyle \underset{i=1}{\overset{m}{\sum }}{n}_i/N_i}$ (3)

当损伤D达到1时，则认为材料将产生疲劳破坏。随机振动响应分析采用的线性的模态叠加法 [12]，得到的直接结果仍然为PSD频谱形式。Steinberg假设上述响应的PSD对应的实际应力历程服从高斯分布，从而采用三区间法对响应的Von Mises应力进行分类 [13]。该方法将应力处理成3个水平：小于1σ应力发生的时间为68.3%，1σ~2σ发生的时间为27.1%，2σ~3σ发生的时间为4.33%。该方法忽略了大于3σ的应力，假定它们不造成损伤。这样，利用Miner定律进行疲劳计算，结构疲劳时间T内的总体损伤计算公式是 [14] [15] [16] [17] ：

$D=\frac{n1\sigma }{N1\sigma }+\frac{n2\sigma }{N2\sigma }+\frac{n3\sigma }{N3\sigma }$ (4)

式(4)中： $n1\sigma \le 0.683\bar{V}T$ (1σ水平的实际循环数目)； $n2\sigma \le 0.271\bar{V}T$ (2σ水平的实际循环数目)； $n3\sigma \le 0.0433\bar{V}T$ (3σ水平的实际循环数目)。同时根据S/N曲线查得的1σ、2σ和3σ应力水平分别对应许可循环的次数 $N1\sigma$ 、 $N2\sigma$ 和 $N3\sigma$。其中， $\bar{V}$ 的表达式如式(5)所示：

$\bar{V}=\left(f\max +f\min \right)/2$ (5)

式(5)中： $f\max$ 、 $f\min$ 分别表示随机振动输入频率的最大值和最小值。

4. 储能柜振动响应和疲劳分析

4.1. 储能柜柜体力学模型

储能柜骨架主要由钢型材(Q235)焊接构成，取整体结构建立有限元力学模型，柜体骨架划分为四边形网格为主，电气部件划分为六面体单元为主，焊缝形式采用rigid单元，螺栓连接采用beam单元，柜体内各吊挂安装电器元件的重量以质量单元的形式进行考虑。图2(a)是柜体的整体有限元模型，该模型共有节点486,877个，单元468,844个。图2(b)为吊耳及电气部件局部图。需要指出的是，有限元电气部件仅能保证质量与真实电气件的质量相同，其刚度和转动惯量并不一样，但相对于简化为质量点时电气件无转动惯量且各个安装点为刚性的情况，安装点附近的应力精度会更高。另外吊耳处采用较大的螺栓连接并施加预紧力，局部刚度很大，因此将吊孔周边垫片范围内的节点与吊孔中心点进行刚性耦合，再对耦合点施加约束。模型的x方向是车体行进方向，y方向为垂向，z方向为横向。

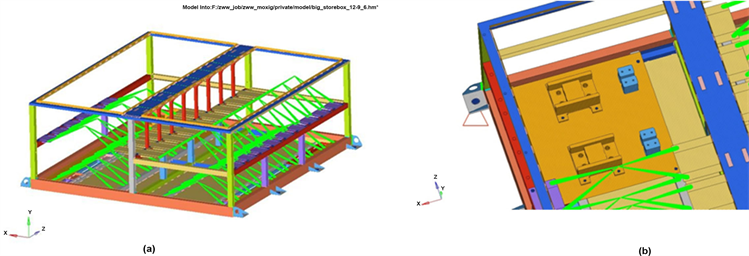
Figure 2. Finite element model of energy storage cabinet. (a) Overall model; (b) Local details

图2. 储能柜体有限元模型。(a) 整体模型；(b) 局部细节

载荷根据IEC61373-2010标准中的试验工况来加载，其中随机振动量级采用模拟长寿命试验中1类A级PSD频谱。约束方式为约束安装座的吊耳孔x、y和z方向的位移自由度。由于自重的影响，冲击分析时y方向将叠加1 g的重力加速度载荷。

4.2. 基于模态叠加法的冲击动力学分析

根据IEC61373-2010标准，试验载荷纵向(X)冲击加速度幅值A为50 m/s²，垂向(Y)冲击加速度幅值A为30 m/s²，横向(Z)冲击加速度幅值A为30 m/s²，持续时间D均为30 ms，同时考虑设备自重影响。

在纵向正反向冲击工况下，正向冲击t = 15.5 ms时，σ_max = 228.6 Mpa，位于中间横梁处，如图3所示位置；在垂向正反向冲击工况下，正向冲击t = 16 ms时，σ_max = 175.2 Mpa，位于吊耳螺栓的安装孔处，如图4所示位置；在横向正反方向冲击，正向冲击t = 15 ms时，σ_max = 103.9 Mpa，位于侧面中间梁处如图5所示位置。3个方向最大应力点随时间的变化历程如图6所示(由于为线性计算，正反冲击计算结果完全一致，因此反向冲击未画出)，且σ_max < 235 Mpa (σ_s(Q235) = 103.9 Mpa)，因此，可判定柜体未发生塑性变形，满足结构强度要求；同时可以发现3个方向冲击加速度达到最大时刻(15 ms)时，结构在惯性力和阻尼的作用下，应力并没有达到最大值(横向由于输出设置原因未捕捉到应力最大时刻点，但最大应力与15 ms差别不大)。

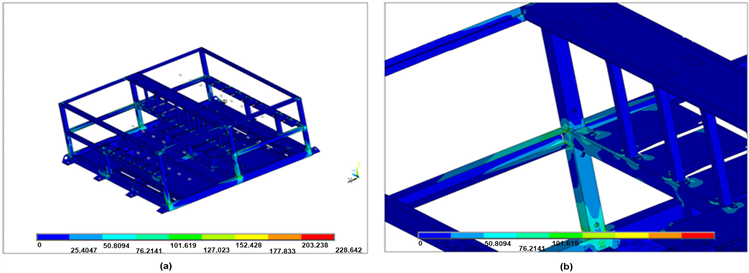
Figure 3. Longitudinal impact strength condition. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (σ_max)

图3. 纵向冲击强度工况。(a) 柜体整体应力；(b) 柜体局部应力分布(σ_max)

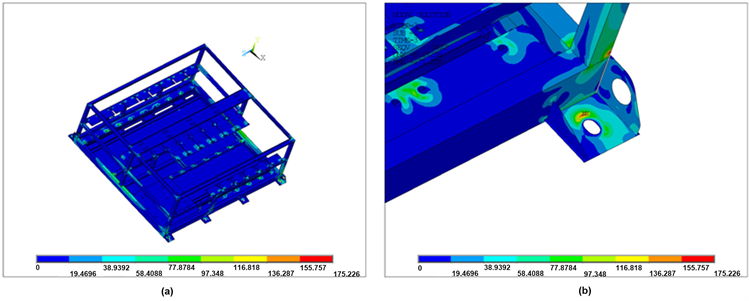
Figure 4. Vertical impact strength condition. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (σ_max)

图4. 垂向冲击强度工况。(a) 柜体整体应力；(b) 柜体局部应力分布(σ_max)

4.3. 随机振动疲劳分析

根据IEC61373-2010标准，储能柜属于1类A级，质量约为1339 kg，依照如图7所示1类A级车体安装设备的ASD频谱，其中，当m < 500 kg时，f₁ = 5 Hz，f₂ = 150 Hz；当500 kg < m < 1250 kg时，

Figure 5. Transverse impact strength condition. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (σ_max)

图5. 横向冲击强度工况。(a) 柜体整体应力；(b) 柜体局部应力分布(σ_max)

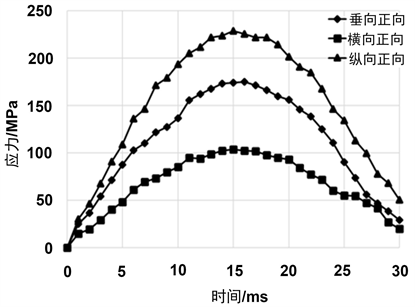
Figure 6. Stress and time curve of impact stress σ_max in three directions

图6. 三个方向冲击应力σ_max的应力时间曲线

$f1=\left(1250/m\right)\times 2\text{Hz}$， $f_2=\left(1250/m\right)\times 60\text{Hz}$ ；当m > 1250 kg时，f₁ = 2 Hz，f₂ = 60 Hz。长寿命试验ASD量级是垂向1.034，横向0.250，纵向0.452 (ms⁻²)²/Hz。所以本储能柜可选取f₁ = 2 Hz、f₂ = 60 Hz的ASD频谱。

纵向、垂向、横向随机振动时1σ应力分布分别如图8~图10所示。纵向随机振动最大应力位于中间横梁焊接处，垂向随机振动最大应力位于中间横梁焊接处，横向随机振动最大应力位于中间横梁焊接处，其1σ、2σ、3σ应力值见表1。

按照Steinberg提出的高斯分布的三区间法，利用Miner定律进行疲劳计算。其中纵向、垂向和横向各试验5 h，即振动时间T = 18,000 s，可以得到储能柜在做随机振动时的振动平均频率为 $\bar{V}=\left(f\max +f\min \right)/2=31\text{Hz}$，则 $n1\sigma =0.683\bar{V}T={{\displaystyle 3.811\times 10}}^5$， $n2\sigma =0.271\bar{V}T={{\displaystyle 7.054\times 10}}^4$， $n3\sigma =0.0433\bar{V}T={{\displaystyle 2.416\times 10}}^4$。根据图11中Q235材料的S/N曲线，在存活率P = 99% 的曲线上查找某一应力值可以得到对应的循环次数。3个方向的1σ、2σ、3σ应力对应的N1、N2、N3见表2。根据式(4)，

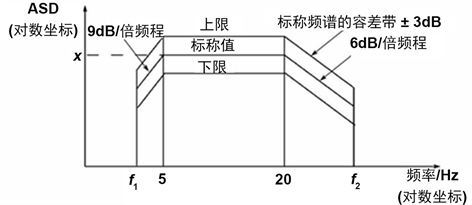
Figure 7. Category 1-Class A-Body-mounted-ASD spectrum

图7. 类–A级–车体安装–ASD频谱

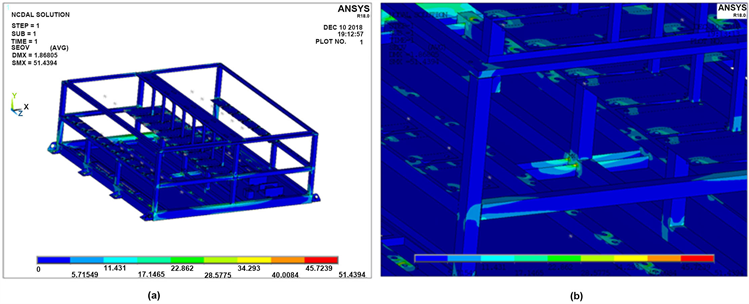
Figure 8. Distribution of 1σ stress in longitudinal random vibration. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (max)

图8. 纵向随机振动时1σ应力分布。(a) 柜体整体应力；(b) 柜体局部应力分布(max)

Table 1. Longitudinal, vertical and transverse random vibration 1σ, 2σ, 3σ stress

表1. 纵向、垂向、横向随机振动1σ、2σ、3σ应力

纵向随机振动时， $D_{纵}\approx 0.007<1$ ；垂向随机振动时， $D垂\approx 0.035<1$ ；横向随机振动时， $D_{横}\approx 0.014<1$。总损伤D = D_纵 + D_垂 + D_横 = 0.056 < 1。

该储能柜完成随机振动试验和冲击试验后，并完成实车测试，未发现明显失效，验证了仿真分析的准确性和可行性。

5. 结论

通过有限元分析软件，应用模态叠加法模拟了储能柜冲击试验过程中的受力情况，结果表明冲击最大应力为228.6 MPa，小于Q235的屈服强度，结构不会发生永久变形，满足设计要求；计算了随机振动

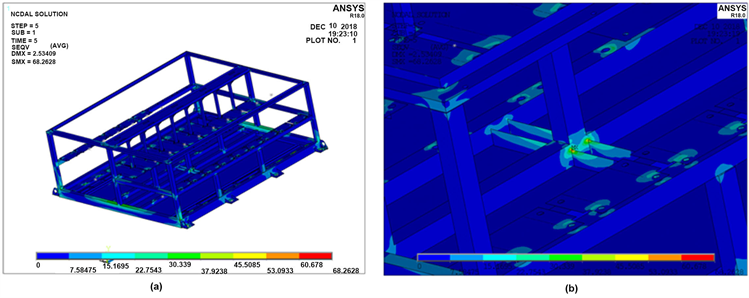
Figure 9. Distribution of 1σ stress in vertical random vibration. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (max)

图9. 垂向随机振动时1σ应力分布。(a) 柜体整体应力；(b) 柜体局部应力分布(max)

Figure 10. Distribution of 1σ stress in transverse random vibration. (a) Overall stress of cabinet; (b) Local stress distribution of cabinet (max)

图10. 横向随机振动时1σ 应力分布。(a) 柜体整体应力；(b) 柜体局部应力分布(max)

Figure 11. S/N curse of Q235

图11. Q235材料S/N曲线

Table 2. The fatigue life under the stress levels of 1σ, 2σ and 3σ in three directions

表2. 在3个方向1σ、2σ、3σ应力水平下的疲劳寿命次数

环境下的响应，得到了结构的1σ、2σ、3σ Von Mises最大应力，并基于高斯分布和Miner提出的线性疲劳累计损伤理论，对结构在给定随机振动环境下的疲劳寿命进行了预估，得到的累积疲劳损伤最大值为0.056，满足疲劳安全设计要求。通过试验和实车验证，产品均可靠运行，确定了该仿真方法的可行性。储能柜柜体作为与安全密切相关的重要结构件，采用有限元仿真进行符合标准的设计校核，能有效指导产品的开发，防止产品设计出现问题导致设计和试验的反复，可加速开发进程，减少开发成本。

NOTES

^*通讯作者。