两类冠图的符号罗马控制数

The Signed Roman Domination Number of Two Classes Corona Graph

摘要: 设图G=(V,E)为一个简单无向图，若S⊆V，则记f(S)=∑_v∈sf(v)。若实值函数f:V→{-1,1,2}满足以下两个条件：1) 对于任意的顶点v∈V，均有f(N[v])≥1成立；2) 如果对任意顶点v∈V，若f(v)=-1，则存在一个与v相邻的顶点u∈V满足f(u)=2，则称该函数为图G的符号罗马控制函数。图G的符号罗马控制数定义为γ_sR(G)=min{f(V)|f为图G的一个符号罗马控制函数}。本文利用构造法及穷标法主要得到了k-正则图的冠图以及轮图的冠图的符号罗马控制数的精确值。

Abstract: Let G=(V,E) be a simple undirected graph and denote f(S)=∑_v∈sf(v) for S⊆V. A real-valued function f:V→{-1,1,2} is called a signed Roman domination function if f satisfies the conditions that 1) f(N[v])≥1 for any v∈V, and 2) every vertex v for which f(v)=-1 is adjacent to a vertex u for which is f(u)=2. The signed Roman domination number of G is γ_sR(G)=min{f(V)|f is a signed Roman domination function f of G} . In this paper, we determine exact values of the signed Roman domination number of two classes graph, such as a Corona of k-regular graph and wheel graph by constructive method and exhaustive method.

1. 引言

本文所指定的图均为无向简单图，文中未说明的符号和术语同文献 [1]。

设 $G=\left(V,E\right)$ 是一个图，其顶点集 $V=V\left(G\right)$ 和边集 $E=E\left(G\right)$。对任意 $u\in V\left(G\right)$，则 $N_G\left(u\right)$ 为u点在G中的邻域， $N_G\left[u\right]=N_G\left(u\right)\cup \left\{u\right\}$ 为u点在G中的闭邻域， $d_G\left(u\right)=\left|N_G\left(u\right)\right|$ 为u点在G中的度，而 $\delta =\delta \left(G\right)$ 和 $\Delta =\Delta \left(G\right)$ 分别为图G的最小度和最大度。在不致混淆情况下，可将 $N_G\left(u\right)$， $N_G\left[u\right]$， $\Delta \left(G\right)$， $\delta \left(G\right)$ 分别简单记为 $N\left(u\right)$， $N\left[u\right]$， $\Delta$， $\delta$。用 $C_n$， $P_n$， $K_n$ 分别表示n阶圈、路和完全图。k-正则图G是指G

中每个顶点度均为k的图。

过去的几十年，图的控制理论作为图论中很重要的研究课题，其研究内容越来越丰富，很多学者在不同背景应用之下提出各种类型的符号控制数以及其变化的形式，如图的符号控制数 [2]、图的边(全)符号控制数 [3]、图的符号全控制数 [4]、图的圈符号(边)控制数 [5] 以及符号(全)罗马控制数 [6]、符号边(全)罗马控制数 [7] [8] 等。在1995年，由J E Dunbar等人首次提出图的符号控制概念，从此开辟了这一研究领域并得到迅速发展。图的符号控制数的研究有着广泛的应用背景，如交通岗位、物资供应点的设置等。

至今为止，很多相关学者踊跃研究关于图的符号罗马控制数的上下界 [9] 以及特殊图的符号罗马控制数的精确值。文 [10] 中，Zhao等人确定了完全二部图以及轮图的符号(全)罗马控制数。文 [11] 中，尹凯等人确定了完全多部图的符号罗马控制数。本文主要确定了两类特殊冠图，如k-正则图的冠图和轮图的冠图的符号罗马控制数。

对于图 $G=\left(V,E\right)$，定义一个函数 $f:V\mapsto R$ 和G的一个子集 $S\subseteq V$，记 $f\left(S\right)={\displaystyle {\sum }_{v\in \in S}f\left(v\right)}$。下文中，为简单起见，记 $V_i$ 表示所有标号为i的顶点集合，其中 $i=-1,+1,+2$。对于 $x\in V$，把 $f\left(N\left[x\right]\right)$ 简单记为 $f\left[x\right]$。

2. 基本概念

定义1 [9] 设图 $G=\left(V,E\right)$ 为一个简单无向图，若 $S\subseteq V$，则记 $f\left(S\right)={\displaystyle {\sum }_{v\in \in S}f\left(v\right)}$。若实值函数

$f:V\mapsto \left\{-1,1,2\right\}$ 满足以下两个条件：

1) 对于任意的顶点 $v\in V$，均有 $f\left(N\left[v\right]\right)\ge 1$ 成立；

2) 如果对任意的顶点 $v\in V$，若 $f\left(v\right)=-1$，

则存在一个与v相邻的顶点 $u\in V$ 满足 $f\left(u\right)=2$，则称该函数为图G符号罗马控制函数。图G的符号罗马控制数定义为 ${\gamma }_{sR}\left(G\right)=\min \left\{f\left(V\right)|f为图G的一个符号罗马控制函数\right\}$。若符号罗马控制函数f满足

${\gamma }_{sR}\left(G\right)={\displaystyle {\sum }_{v\in V}f\left(v\right)}$,

则称函数f为图G的 ${\gamma }_{sR}\left(G\right)$ -函数。

定义2 [3] 图G的每个顶点上粘接r个悬挂点而得到的图称为图G的r-冠图，记为 $I_r\left(G\right)$。特别地，图G的1-冠图，记为 $I\left(G\right)$。

定义3 设 $W_{n+1}=C_n\vee K_1$ 为轮图，其中中心点为 $v_0$，圈 $C_n$ 上顶点为 $v_1,v_2,\cdots ,v_n$。用 $I_7\left(W_{n+1}\right)$ 表示圈 $C_n$ 中每个顶点上粘接7个悬挂点且中心点上粘接 $2n+1$ 个悬挂点而得到的图。

3. 主要定理及其证明

定理1设 $G^{\prime }$ 为任意n个顶点的k-正则图 $\left(k\ge 1\right)$ 且 $G=I_{2k+1}\left(G^{\prime }\right)$，则

${\gamma }_{sR}\left(G\right)=n\left(1-2k\right)$.

证明：设 $G=I_{2k+1}\left(G^{\prime }\right)$， $G=G\left(V,E\right)$，其中 $G^{\prime }$ 为任意的k-正则图。令

$V\left(G^{\prime }\right)=\left\{v_1,v_2,\cdots ,v_n\right\}$, ,

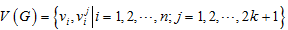其中 $v_i^j$ 为图 $G^{\prime }$ 的悬挂点。下面首先考虑图G的符号罗马控制数的下界。

设 $f=\left(V_2,V_1,V_{-1}\right)$ 是图G的 ${\gamma }_{sR}\left(G\right)$ -函数，由符号罗马控制数定义知

$f\left[v_1\right]+\cdots +f\left[v_n\right]\ge n$,

即

$\begin{array}{l}{\displaystyle \underset{j=1}{\overset{2k+1}{\sum }}f\left(v_1^j\right)}+\cdots +{\displaystyle \underset{j=1}{\overset{2k+1}{\sum }}f\left(v_n^j\right)}+\left(k+1\right){\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left(v_i\right)}\\ =f\left(V\left(G\right)\right)+k{\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left(v_i\right)}\ge n\end{array}$

故，有

$\begin{array}{c}{\gamma }_{sR}\left(G\right)=f\left(V\left(G\right)\right)\\ \ge n-k\left(f\left(v_1\right)+\cdots +f\left(v_n\right)\right)\\ \ge n-k\cdot 2n=n\left(1-2k\right)\end{array}$.

另一方面，通过给出一个符号罗马控制函数g来证明图G的符号罗马控制数的上界。令

$g\left(v\right)=\{\begin{array}{l}+2,当v=v_i,i=1,\cdots ,n\\ -1,否则\end{array}$

容易验证，对于任意顶点 $v\in V\left(G^{\prime }\right)$，有

$g\left[v\right]=2\left(k+1\right)-\left(2k+1\right)=1$.

对于任意顶点 $v_i^j\in V\left(G\right)$，有 $g\left[v_i^j\right]=1$。从而G中有 $\left|V_2\right|=n$， $\left|V_1\right|=0$， $\left|V_{-1}\right|=2k+1$。故，有

${\gamma }_{sR}\left(G\right)\le g\left(V\right)=2\left|V_2\right|+\left|V_1\right|-\left|V_{-1}\right|=n\left(1-2k\right)$.

综上所述，有

${\gamma }_{sR}\left(G\right)=n\left(1-2k\right)$.

定理1 证毕。

定理2 设 $W_{n+1}=C_n\vee K_1$ 轮图且 $G=I_7\left(W_{n+1}\right)$，则

${\gamma }_{sR}\left(G\right)=1-7n$.

证明：设 $G=I_7\left(W_{n+1}\right)$， $G=\left(V,E\right)$，其中 $W_{n+1}=C_n\vee K_1$。令

$V\left(W_{n\text{+}1}\right)=\left\{v_0,v_1,\cdots ,v_n\right\}$

$V\left(G\right)=\left\{v_i^j|i=1,2,\cdots n,j=1,2,\cdots ,7\right\}\cup \left\{v_i^k|i=0,k=1,2,\cdots ,2n+1\right\}\cup V\left(W_{n+1}\right)$,

其中 $v_0$ 是 $W_{n\text{+}1}$ 的中心点， $v_i^j$ 为悬挂点。

设 $f=\left(V_2,V_1,V_{-1}\right)$ 是图G的 ${\gamma }_{sR}\left(G\right)$ -函数，由符号罗马控制数定义知

$f\left[v_1\right]+\cdots +f\left[v_n\right]+f\left[v_{n+1}\right]\ge n+1$,

即

${\displaystyle \underset{j=1}{\overset{7}{\sum }}f\left(v_1^j\right)}+{\displaystyle \underset{j=1}{\overset{7}{\sum }}f\left(v_2^j\right)}+\cdots +{\displaystyle \underset{j=1}{\overset{7}{\sum }}f\left(v_n^j\right)}+{\displaystyle \underset{j=1}{\overset{2n+1}{\sum }}f\left(v_0^j\right)}+4{\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left(v_i\right)}+\left(n+1\right)f\left(v_0\right)\ge n+1$,

由此推出

$f\left(V\left(G\right)\right)+3{\displaystyle \underset{i=1}{\overset{n}{\sum }}f\left(v_i\right)}+nf\left(v_0\right)\ge n+1$.

故，有

$\begin{array}{c}{\gamma }_{sR}\left(G\right)=f\left(V\left(G\right)\right)\\ \ge n+1-3\left(f\left(v_1\right)+\cdots +f\left(v_n\right)\right)-n\cdot f\left(v_0\right)\\ \ge n+1-6n-2n=1-7n\end{array}$.

另一方面，通过给出一个符号罗马控制函数g来证明上界。令

$g\left(v\right)=\{\begin{array}{l}+2,当v=v_i,i=0,1,2,\cdots ,n\\ -1,否则\end{array}$,

容易验证，对于任意顶点 $v\in V\left(W_{n+1}\right)$，有 $g\left[v\right]=1$。对于任意顶点 $v_i^j\in V\left(G\right)$，有 $g\left[v_i^j\right]=1$。从而G中有 $\left|V_2\right|=n+1$， $\left|V_1\right|=0$， $\left|V_{-1}\right|=9n+1$。故，有

$\begin{array}{c}{\gamma }_{sR}\left(G\right)\le g\left(V\right)=2\left|V_2\right|+\left|V_1\right|-\left|V_{-1}\right|\\ =2\left(n+1\right)-7n-\left(2n+1\right)=1-7n\end{array}$.

综上所述，有

${\gamma }_{sR}\left(G\right)=1-7n$.

定理2 证毕。

基金项目

国家自然科学基金(No.11701257、No.11801253)，河南省教育厅高校重点项目(No.18A110025)。