1. 引言
根据解的存在唯一性定理 [2]，如果微分方程
中右端函数
在某区域G上连续，
在G上有界或连续，则在G内初值问题的解是存在且唯一的，
从而在G内肯定不存在奇解。如果存在唯一性定理的条件不在整个
的定义域内成立，则奇解(如
果存在的话)只有到那些破坏了存在唯一性定理条件的点集中去找，也就是到使得
无界的点集中去找。
对于某些微分方程，如
，
等，它们的奇解(包络)是存在的。但是用c-判别曲线法求通解曲线族的包络时，由于通解是在
的取值有一定限制的条件下求得的，所以根据c-判别式求得的c-判别曲线与通解是矛盾的，到目前为止，凡是涉及到求诸如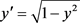
，
之类的微分方程的包络(奇解)问题的书籍、文献(如 [3]、 [4]、 [5] )等，都是在这样的矛盾情形下，逻辑不自洽地“指导出”微分方程的奇解(包络)。结论是正确的，但求解过程是逻辑矛盾的。
本文通过构造通解法解决了这个矛盾。此前笔者曾通过补充定义法解决了这个矛盾(见 [1] )。
2. 构造通解法
例1判断微分方程
(1)
是否存在奇解，如果存在就求出来。
解右端函数
，它在带形区域：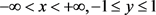
上定义、连续。
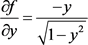
当
时无界，所以方程(1)如果有奇解，只能是
，显然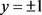
是(1)的两个特解。下面求方程(1)的通解。
当
时(注意这个限制条件)，(1)可改写为
,
积分得
,
于是
(2)
其中c为任意常数。由于
也是(1)的解，故也可把(1)的通解表示为
或
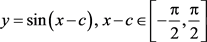(3)
其中C为任意常数。
现在求通解曲线族(3)的包络。这里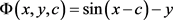
，
，c-判别式为
c-判别曲线为
, 与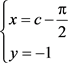
这两条c-判别曲线均为有
，
，满足非蜕化条件，故两条c-判别曲线
都是通解曲线族(3)的包络，从而
都是方程(1)的奇解。
例2 [6] 判断微分方程
(4)
是否存在奇解，如果存在就求出来。
解右端函数
在其定义域内是连续的。
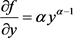
当
时无界，所以方程(4)如果有奇解，只能是
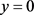，显然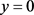
是(4)的一个特解。下面求(4)的通解。
当
时(注意这个限制条件)，(4)可改写为
,
积分得
,
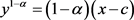或
,
或
,
或
(5)
其中c为任意常数。由于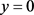
也是(4)的解，故也可把(4)的通解表示为
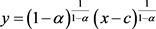, (6)
易得c-判别曲线为
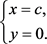
同样易知
为通解曲线族(6)的包络，从而
是(4)的奇解。