基于部分特权信息的支持向量机

Support Vector Machines Based on Incomplete Privileged Information

摘要: 特权信息的重要性在许多领域尤为突出，特别是在生物医学领域。许多研究表明，特权信息可以提高分类的准确性。传统方法是使用SVM+来解决包含特权信息的分类问题。但是在许多情况下，由于特权信息收集成本高昂，训练集仅包含部分特权信息。面对特权信息不完整的数据，最大的挑战是如何使用此部分特权信息来获取数据的隐藏信息。在文章中，我们提出的基于支持向量机(ICSVM+)部分特权信息的新融合分类算法，可以很好地解决这个问题。对此融合分类算法本文提出了两个思想，分别为交叉校正(CC)和线性加权(LW)去实现此融合算法。我们称这两种方法为CC-ICSVM+和LW-ICSVM+。另一项重要工作是，我们提出的基于窗口理论的权重更新方法能够很好地适应不同的数据集。通过与SVM和SVM+的实验比较，我们的ICSVM+方法能够有效地解决特权信息的缺失问题。

Abstract: The importance of privileged information is particularly prominent in many fields, especially in bio-medicine. It is because researchers have proven that privileged information can improve clas-sification accuracy. And the traditional approach usually uses SVM+ to solve the classification problem that contains privileged information. Unfortunately, in many cases the training data set contains only partial privileged information due to the high cost of privileged information collection. In the face of data with incomplete privilege information, the biggest challenge is how to use this partial privilege information to obtain the maximum hidden information of the data. Fortunately, a new fusion classification algorithm based on incomplete privileged information for Support Vector Machine (ICSVM+) that we proposed, can solve this problem well. In this paper, two ideas are proposed for the fusion classification algorithm, namely, cross-correction (CC) and linear weighting (LW). We call these two methods (CC) ICSVM+ and (LW) ICSVM+. Another important work is that a weight updating method based on window theory proposed by us can adapt well to different data sets. Through experimental comparison with SVM and SVM+, our ICSVM+ methods were able to effectively deal with the lack of privilege information.

1. 引言

Vapnik (2009)提出了基于SVM [1] [2] 的新学习范式，即学习使用特权信息(LUPI) [3]，被称为基于特权信息的支持向量机(SVM+)。训练阶段提供特权信息，但不适用于测试集。Vapnik对特权信息做了大量的研究，并且被运用在各个领域中 [4] [5] [6] [7] [8]。实验结果表明，学习使用正确的特权信息有助于提高分类性能 [9]。在某些情况下，特权信息很难收集而且昂贵，特别是在生物学和医学。因此，在实际数据中，有许多情况下只有部分训练样本具有特权信息 [10]。由于SVM+不适合这种情况，我们必须构建一个适应具有部分特权信息的数据集的新模型。部分特权信息类似于通常已知的缺失数据集。对于缺少的数据集，我们现阶段有许多方法完成 [11] [12]。使用其他信息和特权信息的关联来完成缺失的特权信息也是一个可行的方法。这种情况更适合Pu J等人研究的医学数据 [13]。然而，它需要获得特征和标签之间的关系，以补充特权信息的缺失数据，这可能在生物医学中具有更好的实验性能。但在其他领域，特征和标签之间的关系在特权信息中不能很好的体现。因此，这样来补充缺失的数据集可能无法获得稳定的实验结果。

我们不想对原始数据集做大量的填充，而是想要一个好的分类结果。在此情况下，Vapnik习惯于将其放在SVM+的模型扩展部分中，用类似于SVM+的思想来解决它。他使用包含一些特权信息的空间来训练校正函数。与SVM+不同，用于训练校正功能的空间非常小。但缺少特权信息的样本还没有校正。该模型的想法与SVM+的非常相似，理论上它是SVM+模型的较弱版本。基于此理念，我们能否使用具有特权信息的样本空间和没有特权信息的样本空间来相互校正？

事实上，如果具有特权信息的训练集小于原始训练集，则特权信息的影响会非常小。我们可以完全丢弃特权信息不使用SVM训练，而使用SVM+训练。在某些情况下，我们不想丢失任何信息。例如，当具有特权信息的训练集占用原始训练集的30%时，SVM和SVM+都不能实现更好的分类结果。

本文提出了一种基于部分特权信息的名为ICSVM+的融合分类算法。实现此算法需要三个步骤。图1中详细介绍了实施过程。

Figure 1. LW-ICSVM+ and CC-ICSVM+ implementation process. The red box is the two classification methods proposed in this paper. LW is a linear weighted fusion method and CC is a cross-correction fusion method

图1. LW-ICSVM+和CC-ICSVM+实施过程。红框是本文提出的两种分类方法，LW是一种线性加权融合方法，CC是一种交叉校正融合方法

2. 相关工作

特权信息在机器学习中得到了广泛的应用，这是Vapnik在SVM+中首次提出的。后来的研究人员对特权信息在不同的模型上进行了应用 [14] [15]。例如adboost+就是将特权信息用在adboost算法上，以及用在决策树上也有很好的分类性能 [16]。这些方法的原则是利用 $X^{\ast }$ 特权信息产生的空间来校正原始空间X的信息。但是目前对于部分特权信息的数据还有待研究，因此我们将构建有特权信息样本和没有特权信息的样本之间的关系来解决这个问题。构建三个空间 $X^{\ast }$ (特权信息)， $X_1$ (不含特权信息)， $X_2$ 其中 $X_1\cup X_2=X$，利用权重融合去建立空间关系。事实上，权重融合 [17] [18] [19] 可以在很多方面有效地提高实验性能，如神经网络集成。

3. 算法介绍

3.1. 基于SVM的部分特权信息

SVM+实现了具有特权信息的数据分类问题，但没有解决部分特权信息的应用。本文提出的模型称为ICSVM+可以更好地解决问题。当只有一部分样本有可用特权信息，其他n个样本没有特权信息，给定一组三维特征样本：

$\left(x_1,y_1\right),\cdots ,\left(x_n,y_n\right),\left(x_{n+1},x_{n\text{+1}}^{\text{*}},y_{n+1}\right),\cdots ,\left(x_l,x_l^{\text{*}},y_l\right),x\in X,x^{*}\in X^{*},y\in \left\{-1,1\right\}.$

最小化间距由下式给出：

$\begin{array}{l}\underset{\omega ,{\omega }^{\ast },b,b^{\ast }}{\min }\frac{1}{2}\left[\left(w_1\cdot w_1\right)+\left(w_2\cdot w_2\right)+\gamma \left(w^{\ast }\cdot w^{\ast }\right)\right]+C{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\xi }_i}+C^{\ast }{\displaystyle \underset{i=n+1}{\overset{l}{\sum }}\left[\left(w^{\ast }\cdot z_i^{\ast }\right)+b^{\ast }\right]}\\ s.t.y_i\left[\left(w_1\cdot z_i\right)+b_1\right]\ge 1-{\xi }_i,i=1,\cdots ,n\\ y_i\left[\left(w_2\cdot z_i\right)+b_2\right]\ge 1-\left[\left(w^{\ast }\cdot z_i^{\ast }\right)+b^{\ast }\right],i=n+1,\cdots ,l\\ {\xi }_i\ge 0,i=1,\cdots ,n\\ \left(w^{\ast }\cdot z_i^{\ast }\right)+b^{\ast }\ge 0,i=n+1,\cdots ,l.\end{array}$ (1)

其中， $w_1$， $w_2$， $w^{*}$ 由方程定义。

$w_1={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i{y}_i{z}_i},$

$w_2={\displaystyle \underset{i=n+1}{\overset{l}{\sum }}{\alpha }_i{y}_i{z}_i},$

$w^{*}=\frac{1}{\gamma }{\displaystyle \underset{i=n+1}{\overset{l}{\sum }}\left({\alpha }_i+{\beta }_i-C\right)z_i^{*}}$

其对偶问题表述如下：

$\begin{array}{l}\underset{\alpha ,\beta }{\max }{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\alpha }_i}-\frac{1}{2}{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)}\\ -\frac{1}{2\gamma }{\displaystyle \underset{i,j=n+1}{\overset{l}{\sum }}\left({\alpha }_i+{\beta }_i-C\right)}\left({\alpha }_j+{\beta }_j-C\right)K^{\ast }\left(x_i^{\ast },x_j^{\ast }\right),\\ s.t.{\displaystyle \underset{i=n+1}{\overset{l}{\sum }}\left({\alpha }_i+{\beta }_i-C^{*}\right)}=0\\ {\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_i{\alpha }_i}=0\\ {\displaystyle \underset{i=n+1}{\overset{l}{\sum }}{y}_i{\alpha }_i}=0\\ {\alpha }_i\ge 0,i=n+1,\cdots ,l\\ 0\le {\alpha }_i\le C,i=1,\cdots ,n.\end{array}$ (2)

我们获得两个决策函数：

$f_1\left(x\right)=\left(w_1,z\right)+b={\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_i{\alpha }_{i}K\left(x_i,x\right)}+b_1,$ (3)

$f_2\left(x\right)=\left(w_2,z\right)+b={\displaystyle \underset{i=n+1}{\overset{l}{\sum }}{y}_i{\alpha }_{i}K\left(x_i,x\right)}+b_2.$ (4)

决策函数 $f_1\left(x\right)$ 是从没有特权信息的样本中获取的，决策函数 $f_2\left(x\right)$ 是从特权信息样本中获取的。

Figure 2. Process for dealing with the missing of privileged information

图2 .处理特权信息缺失的流程

在最终获得决策算法之前，本文提出了一种基于滑动窗口的权重更新算法。它将有助于完成融合决策的两种部分特权信息的SVM+算法，我们称之为LW-ICSVM+和 CC-ICSVM+。图2显示了方法LW-ICSVM+和CC-ICSVM+方法的实现过程。

3.2. 权重评估

权重选择对于进行融合决策非常重要。在我们的实验中，我们发现基于滑动窗口的权重更新公式非常有效。

在训练集中，样本标签是已知的，我们将训练集划分m块，并表示为 $d_j\left(1\le j\le m\right)$。对每个数据块使用上述模型，我们发现两组决策函数的值， $f_1^j$ 以及 $f_2^j$ 最佳权重可以通过以下公式获得：

$q^j=\underset{0<q<1}{\text{arcmax}}F\left[q{f}_1^j+\left(1-q\right)f_2^j\right]$ (5)

其中， $F[\cdot ]$ 是这组决策值的准确率。

这些数据块中会有一些数据块，即使调整了参数，精度也不会很高。我们需要省略与这些数据块对

应的参数。因此，我们将设计一个窗口W，并且窗口中的数据块数是固定的( $W={\displaystyle \underset{s=1}{\overset{u}{\cup }}{d}_s}$ )。每次输入新的

数据块，计算最佳参数及其相应的精度，记为 $\left(q^j,A^j\right)$，其中 $A^j$ 是精确率。比较原始窗口中权重的精度，并删除精度最低的相应权重(如果精度相同，则随机删除一个权重)，最后平均值q将作为最终权重。权重更新的步骤在算法1中给出。在图3中，我们显示了原始窗口与新窗口之间的关系：

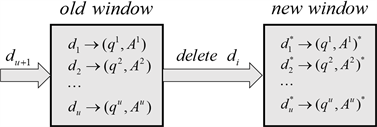
Figure 3. Weight value evaluated by a slide window

图3. 滑动窗口计算的权重值

窗口大小为u，下一步我们的新窗口将成为旧窗口。

3.3. 融合方法

3.3.1. 线性加权融合法

线性加权融合获得的新决策函数为：

$f\left(x\right)=q{f}_1\left(x\right)+\left(1-q\right)f_2(x)$

等价于：

$f\left(x\right)=q{\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_i{\alpha }_{i}K\left(x_i,x\right)}+\left(1-q\right){\displaystyle \underset{i=n+1}{\overset{l}{\sum }}{y}_i{\alpha }_{i}K\left(x_i,x\right)}+\left(1-q\right)b_2+q{b}_1$ (6)

3.3.2. 交叉校正融合

在半监督学习中，有一类自训练算法 [20]。该算法将测试集的置信部分返回到训练集进行再训练，直到所有测试集都分类。运用这个思想将测试集转换为训练集，提出了交叉校正融合方法。该方法可以得出一系列伪标签，删除不好的分类结果，保留较好的分类结果。与Vapnik的想法不同，我们的方法是双向相互修正，而不是单向修正。交叉校正融合方法有两个步骤：分配步骤和校正步骤。

标签预分配：

在ICSVM+模型中，我们不仅得到两组决策值，而且得到两组标签 $L_1$ 和 $L_2$。以 $L_2$ 为对象，我们可以获取n组伪标签 $L_2^1,L_2^2,\cdots ,L_2^n$ (算法2中显示了算法步骤)。

标签校正

在监督学习过程中，通常数据集分为训练集和测试集，训练集用于生成分类器，测试集用于测试分类器的效果。在这里，我们添加一个验证集。从理论上讲，完整的数据集可以达到良好的分类效果，但当训练集有错误的数据(训练标签错误)时，测试集会得到一个坏的标签，从而降低分类精度。在这个问题上，我们提出了交叉校正融合方法(CC)，以选择 $\left(L_2^1,L_2^2,\cdots ,L_2^n\right)$ (上一步)中的最佳标签。

CC通过以下步骤实现：

步骤1：将 $L_2^i$ 分配方法中的标签和测试集合并到新的训练集中，记为 $D_{train}^i$。

步骤2：从验证集中选择k个样本为新测试集，该测试集记为 $D_{test}$，其标签记为 $L_{test}$。

步骤3：由于分配步骤的测试集没有特权信息，我们使用SVM来训练训练集 $D_{train}^i$ 和测试集， $D_{test}$ 并将预测标签标记为 $L_{test}^{*}$。然后，将步骤3中的标记与步骤2中的标记进行比较，并将获得的准确率标记为 $a_i$。

步骤4：重复上述步骤以获取对应于n个伪标签 $L_2^1,\cdots ,L_2^i,\cdots ,L_2^n$ 的n个准确率 $a_1,\cdots ,a_i,\cdots ,a_n$。选择准确率 $a_j=\underset{1\le i\le n}{\max }{a}_i$，其相应的标签 $L_2^j$ 是最佳标签。

关于CC的实现步骤，我们在算法3中给出了。在CC中，我们没有在分配步骤中将测试集添加到具有已知标签的训练集中，这与半监督学习的自训练算法不同，因此很难选择最佳标签。同样，我们试图在步骤2中放大k的值以放大精度之间的差异并选择最佳标签。因此，在CC实现过程中，数据集实际上是分批测试的，输入数据块不应太小，这样会降低SVM的精度，也不应该太大，太大会增加计算量。

3.4. 数据块大小控制

在CC-ICSVM+中，我们需要选择最佳标签。预测标签的数量是分配步骤中的随机次数。因此，为了节省计算量，我们将尝试减少上述算法中的n。通过随机选择，如果所有可能的组合都取到，则一定可以得到最优标签。在某些情况下，获得最优标签的成本非常高。实际上，我们也可以选择次优标签。如果输入的测试数据块较大，这样导致随机次数也会增加，因此可以使用批量处理测试来节省计算量。从以下不等式可以看出，对较大测试集的批量处理测试将节省计算量。

$C_{\left|l_1\right|+\left|l_2\right|}^{r_1+r_2}>C_{\left|l_1\right|}^{r_1}+C_{\left|l_2\right|}^{r_2}$ (7)

4. 实验设置

4.1. 实验准备

从UCI数据集中选出了八个数据集：Wine data set, seeds data set, Pima Indian Diabetes data set, lonosphere data set, Abalone data set, statlog (heart) data set, Breast cancer Wisconsin data set, Liver Disorders data set。8个数据集的样本数量不同，为了统一化，我们从8个数据集中提取了部分数据集且大小近似，并将数据集的这一部分划分为训练集、测试集和验证集。训练集与测试集的比率为7:3。此外，将训练集分为两部分：特权信息和非特权信息也就是普通特征，然后分析特权信息样本比例的准确性影响。表1提供了八项实验数据的详细信息。

Table 1. Information about experimental data

表1. 有关实验数据的信息

在实验过程中，我们选择了4种方法：SVM、SVM+、LW-IC SVM+、CC-ICPSVM+。在前两种方法中，数据无法充分利用。包含特权信息和没有包含特权信息的样本将分别在SVM和SVM+中丢弃。值得注意的是，由于特权信息有助于分类，因此在真实数据中可能会丢失更多特权信息。尽管SVM训练样本比SVM+训练样本多，但准确率不一定高于SVM+。

4.2. 实验结果

在LW-ICSVM+中，我们使用了线性加权融合方法，而在CC-ICSVM+中，我们使用了交叉校正融合方法。在表2中，当特权信息争用占训练总量的30%时，我们分别使用四种方法获得八组数据的准确率。在实验过程中，30%的特权信息在训练集中随机提取，因此训练集中的部分示例不包含特权信息。在这里，我们随机抽取了3次，最终准确率被平均。我们可以看到，对于八组数据集，LW-ICSVM+和CC-ICSVM+方法均高于SVM和SVM+，尽管SVM和SVM+在某些情况下工作良好。对于Wine data set，seeds data set，LW-ICSVM+方法优于CC-ICSVM+。原因有两个：首先，因为CC-ICSVM+对两个分类器进行相互更正。如果一个分类器的所有训练点的错误也是另一个分类器的训练点错误，则CC-ICSVM+方法将不能得到准确的结果。其次，由于这两组数据集的样本数量几乎很少，而且新的测试集我们在校正步骤中产生的测试组也相对较小。因此，它导致校正步骤的精度差别很小，并且无法明确选择最佳标签。

Table 2. Experimental accuracy of eight groups of data

表2. 八组数据的实验准确率

对于方法 CC-ICSVM+中的校正步骤，我们知道每组预测标签对应的准确率，对应的最高准确率的标签是最佳标签。表3显示了Breast Cancer Wisconsin and Ionosphere datasets中每个预测标签 $L_2^i$ 的准确率。在分配步骤中，我们取n = 5，获取5组伪标签， $d_2$， $c_1$ 为最佳标签。

Table 3. The accuracy a i of each prediction label L 2 i

表3. 每个预测标签 $L_2^i$ 的准确率 $a_i$

5. 结论

对于训练集只包含部分特权信息的情况，以及几种研究提出的不同的方法，但其性能和结果并不高。我们提出了LW-ICSVM+和CC-ICSVM+算法，有效地解决了特权信息不完整的问题。在实现过程中，我们采用了自适应权重更新公式的思想。实验表明，与传统SVM和SVM+相比，该方法的准确率显著提高。在比较LW-ICSVM+与CC-ICSVM+时，我们发现虽然后者的准确率高于前者，但前者的复杂性更低。因此，如果分类精度不需要很高，可以选择LW-ICSVM+。最后，对于算法测试的复杂度上，在CC-ICSVM+中提出了对测试集的分区，以控制算法的计算量。

在未来的工作中，我们计划控制CC-ICSVM+的计算量，合理控制测试集数据块的大小，对数据块的大小与分类准确率之间的关系进行实验研究，从而获得能够保证在拥有较少的计算量的情况下产生较高的精度。