1. 线
线若要在四维世界中存在,则必须要有体积(具有一到三维的量)和时间(第四维的量)。我们在研究一条线时,往往无视其他参数。而线长度的本质是什么?在一般研究线时,往往会对线的宽度忽略不计(也就是所研究的线都一样长,不是无限趋近与零)。但线宽是线的性质,没有线宽则线也不存在。而一条宽度无限小的线的本质是什么?现在,在研究线时加入宽度。设宽度为x时,y单位长度的线有y单位体积。我们先画一条线,它有2y单位长度,2z单位体积如图1。

Figure 1. A line with a width of x, a length of 2y and an area of 2z at 30˚ from the reference line
图1. 与基准线成30˚的宽度为x,长度为2y,面积为2z的线
将这条线以与基准线(图中虚线,在图中与线的夹角为30˚)方向平行的方向无限切割,如图2。
将切割后的每一份沿基准线方向平移,移动到与基准线方向垂直的同一条直线上,其拥有2y单位面积,y单位长度,和2x单位宽度。宽度的计算方式如图3所示。
这两条线理所当然不同,它们的差别在哪?在切割的过程中两条线相对的每一份的面积都不同,这是为什么他们长度不同,宽度不同,体积相同。也就是移动后两条线的宽度不同,是因为宽度的不同导致面积相等。在宽度都为一个定值时,长度不同时面积一定是不同的。但当宽度无限小时,这时切割后的每一份都是一个面积无限小的点,这时,宽度的差别就消失了,两条线相对的每一份的面积都相同了。体积等于份数 × 每份的面积,份数相同,每份体积相同,这两条线的体积相同。这两条线的长度不同一条为2y另一条为y,宽度相同(都无限趋近于0),体积却相同了。
曲线仍是如此,画一条曲线,如图4。

Figure 3. After cutting, a line with a width of 2x, a length of y and an area of 2z which is 90˚ to the reference line is formed
图3. 切割后形成的宽度为2x,长度为y,面积为2z的与基准线成90˚的线
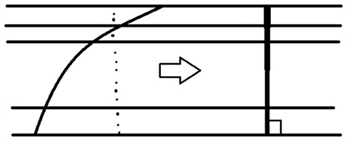
Figure 4. A curve cut in the same way
图4. 以同样方式切割的曲线
按照上文方法切割,然后平移,在曲线宽度为x时,它切割后会变成一根不均匀的线,如图五。在宽度无限小时,每份间的差别也消失了,每一份都是一个无限小的点。体积等于份数 × 每份的面积,份数相同,每份体积相同,这两条线的体积相同,所以曲线也仍是如此。
2. 维度
零维和一维的差别是长度,一维和二维的差别是面积,二维和三维的差别是体积,三维和四维的差别是时间。如果仅仅只拥有三维的一个物体,它是不会变化的(包括所有的性质)。只拥有三维的物体就像是一张三维立体成像的照片,它的一切已经被固定。而在四维中,三维拥有变化这种性质,这就像是电影,不过是完全3D的。它由一张张连续的照片拼接而成。所以我们可以这样构造四维:在三维外,建立一条坐标轴,轴上的每一点都是一个完整的三维世界,连续的三维世界相互连接才能展现出变化的性质。一维,二维,三维都是这样,只有在更高维中,内部的维度才可以变化 [1]。也可以这样想象,无限切割时间(虽然在现实世界不能无限切割),大家都能想象的到,在静止的时间中所有的物体都是静止的。在前文关于线的理论中,宽度无限小的线由无限小的点叠加而成,并且每条这样的线都具有相同面积。这就像维度一样,每一个维度世界在较高维中总是有相同意义,这种构造完全符合维度的性质。反过来推也仍然成立,一个三维世界无限分割后每一份都是一个面,把面无限分割每一份都是线,把线无限分割每一份都是一个点。由此,我们可以推测:较高维是由较低维(比前者低一维)无限叠加而成。
现在,我们用上文切割的方式证明该种构造适应于所有维度:
我们把线放在三维中,以任意方向无限切割。切割后的每一份仍然是无限小的点。由于其在三维中拥有体积,份数相同,每份体积相同,整条线的体积相同。由这样的线叠加的面,由于其中的每条线都有这样的性质,所以每个这样的面体积也相同。
我们再把线放在四维中,以任意方向无限切割。切割后的每一份仍然是无限小的点。由于其在四维中拥有四维积,份数相同,每份四维积相同,整条线的四维积相同。由这样的线叠加的面,由于其中的每条线都有这样的性质,所以每个这样的面体积也相同。由这样的面叠加的体,由于其中的每个面都有这样的性质,所以每个这样的体四维积也相同。
接下来,剩下的维度同理可得,就不再多做叙述了。这是和无限切割理论相辅相成的,它们相互为基础相互证明。
3. 点线面循环
由于维度的无限叠加理论,我们会发现一个现象:点形成线,线形成面,面形成体,体连起来又是一条线,线又形成面,面又形成体,体又形成线……维度的形成一直是点线面–点(体点)线(体线)面(体面)–点线面这样的循环。其本质在于线性的堆叠,线性的堆叠导致了点线面循环的现象。
4. 量不变原理
我们把线放在一维中,以任意方向无限切割。切割后的每一份都是无限小的点。份数相同,每份长度相同,整条线的长度相同。由这样的点叠加的线,无论是怎样的,其长度都可以说是相等的。
我们再把线放在二维中,以任意方向无限切割。切割后的每一份仍然是无限小的点。由于其在二维中拥有面积,份数相同,每份面积相同,整条线的面积相同。由这样的线叠加的面,由于其中的每条线都有这样的性质,所以每个这样的面的面积也相同。这样的面每一个都是面积相等的。而依照前文的切割方式,这样的线本身也是面积相等的。
其他维度同理可得。
我们可以发现同维度的维度有相同的量(在无限可分的情况下),再结合上文中维度的理论,也就是维度在较高维中代表的量相等。这些量不变就构成了量不变原理。量不变原理也因此分为两种:维度间量不变,维度内部的量不变。维度间量不变就是维度在较高维中代表的量相等,维度内部的量不变就是同维度的物体具有相同的量(在无限可分的情况下)。这就是量不变原理。
5. 量不变原理在现实中的应用
5.1. 维度内部量不变原理
由于存在空间离散性,所以维度内部并不能无限切割。因此维度内部的量不变原理在现实中是不成立的。但我们可以反过来利用这种不成立。如果我们所生活的世界中一种量是无限可分的,那么根据维度中的量不变原理,这种量一定不能表示为一个确切的数字。所以只要是可以用确切数字表示出来的物理量都一定是存在离散性或者叫量子性的性质。这就意味着每一个可以用确切数字表示的物理量一定有一个最小量,现代我们以及发现了许多这样的量。例如能量子,元电荷,以及空间时间的离散性。现在,通过维度中的量不变原理我们逆推出:力,磁场等也具有这样的性质。它们一定有最小量,而它们的量是最小量的整数倍。
5.2. 维度间量不变原理
由于维度世界中存在空间离散性,所以维度内部无法无限分割。然而在维度之间,较高维看较低维都是视作无限可分的。这就像是生活在影片中的一个物体,影片的最小单位是一帧,在一部影片中,一帧拥有一个固定的时间n秒,对于生活在其中的东西,这就是它们的离散性,是一种性质,无法再分。而对于我们可以编辑影片的人来说,它仍然是可分的,在n秒中我们还可以再加任意帧,还是n秒但帧数已经完全不同。在维度世界中可以无视较低维(比前者低的任意维)的空间离散性,这就是维度间的无限可分。这也是为什么维度中量不变原理在现实世界中不成立而维度间量不变原理成立的原因。
5.3. 由量不变原理得到基本公式
现代科学家们已经发现在高维中,某些公式可以统一。这说明物理量是遵循着和维度有关的某些法则的。而且,世界本身也是由维度构成。那么,综上所述,维度的法则即是世界的法则。我们可以推测物理量也遵守维度的法则,即上文叙述的量不变原理。
由于离散性,维度内的物体不能无限分割,而是可以表达为一个确切的数字。且由于维度间的无限可分,维度间量不变原理仍然成立,所以我们得到公式。在高维量不变的情况下,所有低维量的乘积不变(乘积即是维度的变化,线乘线就是面积,线乘面就是体积,线乘线再乘线还是体积,低维量的相乘就构成了高维)。这就组成了公式。例如:对应着面积不变的公式xy = z也就是x,y所代表的物理量的乘积一定等于z,在z不变的情况下,xy一定等于一个定值。当然,z本身是可以变的。x增大,y就减小;y增大x就减小。视为一个量是基础量,而另一个量是它线性叠加的值,总量等于一个定值。
5.4. 公式循环
由于点线面循环,公式的变化又遵循图形的变换(维度的变换),所以所有基本物理公式都可以表达为
 (x,y,z,n都代表不同的一个物理量,三个公式之间没有相互关系,三个公式中的x,y,z
(x,y,z,n都代表不同的一个物理量,三个公式之间没有相互关系,三个公式中的x,y,z
可以代表不同物理量。此公式只代表形式)的形式分别代表着面积不变,体积不变。线本身只是一个量,不足以成为公式,体到线的变化就是这样没有公式,所以只有以上的那3种公式。
5.5. 量不变推导出的量的离散性
根据维度内部量不变原理,一个可以无限分割的量,无论怎样量都相等。这就意味着这个量无法用确切数字表达。逆推,如果一个量能够用确切数字表达,那么它一定是无法无限切割的,这代表它一定具有离散性或者是量子化(能量子等)的性质。已经发现的就有许多这样的例子:空间离散性、能量子、元电荷电量等等。因此我们可以预言力,质量以及其他量的离散性存在(力量子,质量子等)。
5.6. 时间流动即是位移
如果,我们的世界是绝对静止的,那么一个在我们世界相对我们世界静止的物体就一定不据有能量,它的能量为0焦耳。但是,爱因斯坦等科学家们已经推导出了物质和能量的转化关系
,说明在现实世界中,静止的物体也具有能量。那么,我们的世界就一定是按照一个固定速度不断运动的。所以,我们建立一个绝对静止的坐标,而我们的世界在该坐标系中移动。而且由于我们的世界是在不停运动的(前几句的论证),又由于不同的世界不可能在该坐标系的同一点上(众所周知,一个坐标只能有一个数据,就像一个固定的时间点上只能有一帧)那么时间的流动就代表着空间的流动(就像照片组成的电影一样)。也只有这样,一个在我们世界静止的物体才能有能量。而我们在空间中的位移基于该移动之上,所以会在绝对静止坐标系中和世界产生偏差造成时间流动不同的现象(如下文的解释)。
5.7. 用量不变原理和无限叠加原理对洛伦兹变换以及相对论的解释
由于无限叠加原理,四维由三维无限叠加而成,既然四维世界可以稳定的运行,那么,三维世界的变化(在内部物体都静止的情况下,也就是前文中在绝对静止坐标系中世界的移动)就一定有一个稳定的速度。就像一部影片的帧率。这种速度在四维世界中就是时间流动的速度。
洛伦兹变换是以
[2] 的方式变换,我们可以将它变换一下
根据量不变原理
,在这种空间中v (这里是
(能应用与洛伦兹变换的所有量)一定是一个定值。
那么,我们是否可以这样认为:在空间中静止的某一物体,时间在该物体上流动的速度是光速c。而在空间中位移的物体使时间在其身上流动的速度改变为
,
(可以视为在四维中空间的方向被扭曲成前后两个方向,也就是一个空间矢量变成了标量)。根据量不变原理(以时间为例)时间在该物体上流动的速度 × 普适时间 = 普适时间流动的速度 × 该物体真实经历的时间。也就是该物体在时间线中经历的位移一定和一个静止物体在时间线中经历的时间相等。
接下来是对
[3] 的解释,设一静止(在我们世界静止)的物体上有一力F作用在上面,该物体
质量为m,力的作用时间是t,力作用的距离为s。那么能量就是E = FS,动量P = Ft,则
转化一下就是
。在瞬间,时间间隔极短可以视为F大小不变的情况,即
即瞬时能量为
(v是
也是该点的瞬时速度,不考虑相对论质量变化)。而如果以诞生(没有加速
过程,平均速度就是最终速度也是瞬时速度)的方式能量就会不同。这时
,这时
(v是诞生后的速度)而我们的世界遵守着
的规律,这更是印证了世界流动的速度是v,也与前文时间流动即是位移以及洛伦兹变换的解释相互论证。
这就是使用量不变对相对论解释的一种有一定理论论证的推导猜想。
6. 结论
1) 高维可以由低维线性的无限叠加而成。
2) 同一维度的任何物体在较高维度中拥有相同的量。
3) 在可以无限分割的情况下,同一维度的任何物体在其维度拥有相同的量,且该量无法用确切数字表达。
4) 前一条的逆推,在现实中,可以用确切数字表达的物理量一定是离散型的。
5) 因为量不变和无限叠加,所以形成了规律(公式)。
6) 所有的基本物理学公式都可以表达为
(x,y,z,n都代表不同的一个物理量,三个公
式之间没有相互关系,三个公式中的x,y,z可以代表不同物理量。此公式只代表形式)的形式。
7) 依靠前几条的结论来对洛伦兹变幻的解释。