1. 引言
从20世纪初开始,金融分析逐渐发展,1952年均值–方差投资组合理论的提出,标志着标准金融学的诞生。标准金融学以投资者完全理性和有效市场假说为前提,研究并开发出了一系列资产定价模型,比如资本资产定价模型(CAPM)以及其各种拓展形式和多因素模型等 [1] [2]。Fama和French于1993年在他们的《股票和债券收益的共同风险因素》一文中提出了著名的三因素模型 [3],至此之后,标准金融资产定价理论迅速发展并成熟,行为金融学应运而生。行为金融学针对标准金融学中投资者完全理性与有效市场的假设前提,提出了不同的观点 [4]。首先是引入了投资者不完全理性 [5] 的假设,认为市场参与者不完全是理性的,他们只是准理性人或者有限理性人,当他们做出风险决策时,并不遵循贝叶斯规则,而是使用简单有效的直观推断。然后提出了有限套利的观点,认为市场由于非理性交易者的存在,会导致不当定价,因而会存在套利机会,因此,有效市场假说可能是无效的。投资者的不完全理性和限制套利的存在构成了行为金融学的理论基石 [6] [7] [8]。
我国现实的金融市场中,由于每一个投资者的生活经历、受教育水平以及所拥有资产都不尽相同,所以异质性的存在是一定的,同时异质信念也是金融市场的一个重要特征。
2. 异质信念的相关理论
衡量异质信念的主要指标有分析师预测分歧、收益波动率和换手率等 [9] [10] [11] [12] [13]。
1) 在异质信念与资产收益关系的实证检验中,分析师预测分歧是最基本的衡量指标,一般用分析师收益预测的标准差来表示,分析师预测的分歧程度与未来收益负相关。
2) 收益波动率又称历史波动率,因为它反映了股价过去的波动,但是因为股价波动难以预测,利用历史波动率来对价格进行预测一般来说都不能保证准确。其计算方法为:首先从市场上获得股票在固定时间间隔上的价格;其次对于每个时间段,求出该时间段末的股价与该时段初的股价之比的自然对数;最后求出这些数值的标准差,再乘以一年中包含的时段数量的平方根,得到的结果即是历史波动率。
3) 换手率是指一年内股票的成交量占股票总数的百分比 [14]。其计算公式为:换手率 = (某一段时期内的成交量)/(发行总股数) × 100%。
股票的换手率和超额收益波动率是异质信念的较好衡量指标,与分析师预测值的分歧度呈较强的正相关,异质信念越强的股票,后期收益率越低,并且这个现象只有在卖空限制存在时才显著。股票收益波动率除了受到异质信念的影响之外,还受到市场风险、公司规模等因素的影响。
3. Fama-French三因子模型与改进
3.1. Fama-French三因子模型
Fama-French三因子模型认为,一个投资组合(包括单个股票)的超额回报率可由它对三个因子的暴露来解释,这三个因子是:市场因子(
)、市值因子(SMB)、账面市值比因子(HML) [3]。
其中市场因子表现为每月回报率与无风险回报率之间的差异;市值因子表示为小规模公司收益与大公司收益之差;市值比因子表示为高净值市价比公司股票收益与低净值市价比公司股票收益之差。
这个多因子均衡定价模型可以表示为:
其中
表示为时间t的无风险收益率; 表示为时间t的市场收益率;
表示为时间t的市场收益率; 表示为资产i在时间t的收益率;
表示为资产i在时间t的收益率; 是市场风险溢价即市场因子;
是市场风险溢价即市场因子;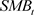 为时间t的市值因子的模拟组合收益率,
为时间t的市值因子的模拟组合收益率, 为时间t的账面市值比因子的模拟组合收益率,
为时间t的账面市值比因子的模拟组合收益率, 、
、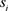 、
、 分别是三个因子的系数。需要注意的是假若所实证数据完全满足这个模型,则截距应显著为0。
分别是三个因子的系数。需要注意的是假若所实证数据完全满足这个模型,则截距应显著为0。
在探讨Fama-French三因子模型的应用时,是以“有限理性”理论假设为基础,同时FF三因子模型属于多元回归模型 [3]。其基本假设为:
1) 、SMB、HML与随机误差项u不相关;
、SMB、HML与随机误差项u不相关;
2) 零均值假定: ;
;
3) 同方差假定,即 的方差为一常量:
的方差为一常量: ;
;
4) 无自相关假定: ;
;
5) 解释变量之间不存在线性相关关系,即两个解释变量之间无确切的线性关系;
6) 假定随机误差项 服从均值为零,方差为
服从均值为零,方差为 的正态分布,即
的正态分布,即 。
。
3.2. 三因子模型实证研究
3.2.1. 数据及其处理说明
本文数据选用2010年6月1日到2015年12月31日期间沪深A股上市的其中100支股票,数据来源为东方财富choice数据库。
首先我们对所选取的100支股票进行分类,以流通股份数额为标准,进行从小到大的排序,分成小、大两类;然后根据账面市值比即股东权益与公司市值之商的值进行从小到大的排序,分成低、中、高三类;再对这两种分类取交集,得到SL、SM、SL、BL、BM、BH六个投资组合 [15]。
月收益率的计算采用每只股票每月的收盘价减去开盘价之差再除以开盘价的值。
具体因子计算公式如下:


市场因子的值 ,为所有股票样本的月收益率加权平均的值减去无风险收益率得到,其中无风险收益率我们采用当月的利率进行计算。
,为所有股票样本的月收益率加权平均的值减去无风险收益率得到,其中无风险收益率我们采用当月的利率进行计算。
投资组合的市场收益率 的值为投资组合中所有股票的月收益率加权平均所得,公式表示为:
的值为投资组合中所有股票的月收益率加权平均所得,公式表示为:

其中 表示预期收益率,
表示预期收益率,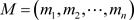 表示无风险收益率,
表示无风险收益率, 表示市场因子的矩阵,
表示市场因子的矩阵,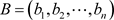 表示市值因子的矩阵,
表示市值因子的矩阵, 表示市值比因子的矩阵。
表示市值比因子的矩阵。
3.2.2. 三因子模型数据处理
首先计算每只股票的月收益率,部分结果如下表1所示。

Table 1. Monthly yield of stock samples (Partial)
表1. 股票样本的月收益率(部分)
需要注意的是,一是其中为0的部分,是因为其月开盘价等于其月收盘价所致;二是号码是指对每只股票进行了编号以便方便计算。
而后根据流通股数的排序将所有股票分成S和B两类,又根据账面市值比将所有股票分成H、M和L三类,接着组合得到SL、SM、SL、BL、BM、BH六个投资组合,部分结果如下表2、表3所示:


Table 2. SL combinations (Partial)
表2. SL组合(部分)

Table 3. BM combinations (Partial)
表3. BM组合(部分)
其中的数字为股票的编号,说明此股票在这个投资组合中。
再进行三个因子的计算,分别是市场因子、市值因子(SMB)以及市值比因子(HML),部分结果如下表4所示:


Table 4. Values of three factors (Partial)
表4. 三个因子的值(部分)
最后对三因子进行拟合得到四个参数的结果如表5所示:

Table 5. Three-factor model parameter values
表5. 三因子模型参数值
根据FF三因子模型的研究,如果模型能完美解释数据的话,则beta1 > 0, beta2 < 0, beta3 > 0, beta4 = 0。
但是从表5我们可以看出所有的投资组合中beta1都大于0,且数值的绝对值都最大,说明市场因子的解释能力最强且起正面作用,符合FF三因子模型的研究结果。而beta2的值在SH、SM、SL中都大于0,与FF三因子模型研究结论相符,但是在BH、BM、BL中beta2的值小于0,即在中国股市上大盘股的市值因子小于0,说明在中国股市上大盘股的市值因子反而起了负面作用,与FF三因子模型的研究结果不相符。beta3的值在SH、BH、BM中都大于0,符合FF三因子模型的研究,但在SM、SL、BL中的值都小于0,与FF三因子模型的研究结论不相符,beta3的值说明中国股市的实际情况是全部高价值和部分中价值的股票与FF三因子模型的研究结论相符合,即市值比因子起了正面作用,而小盘股的中价值和所有低价值的股票都不符合,即市值比因子起了负面作用。所有投资组合的beta4即常数项都很接近于0,符合FF三因子模型的研究结论。
每个模型的拟合度以及p值等如下表6所示:

Table 6. The coefficient of determination and p-value of the portfolio
表6. 投资组合的判定系数、p值
我们可以看出每个组合的模型拟合度都高达90%左右,效果十分理想,但是如此高的拟合度可能存在多种共线性的问题,但是在这里我们暂时不考虑。而p值远远小于0.05,模型十分显著。
3.3. 三因子模型的改进
虽然我们从上面的数据实证可以看出三因子模型已经十分显著了,但是还能进一步改进。改进的意思并不只是单单提高拟合度,而是在允许拟合度相差不多的情况下,给投资者更多的选择,即投资者在投资的过程中,如果选用三因子模型,就只能去关注和研究市场因子,市值因子以及市值比因子相关的数据和讯息,这会造成一种选择的固化。也即,投资者没有多余的选择,选择不够多样化。假如所有的投资者都看重了三因子模型的拟合度,而都选择了使用三因子模型来预测收益,那么所有人的收益和损失都是一样的,每个人都没赔没赚,整个股市无法运行。但是如果有了多种选择,即使模型的拟合度稍微低了一点,也会有人去选择这种模型,因为不可能每只股票都满足三因子模型,总有一些股票满足新的模型,这样便能让整个股市流动起来。
这里我们采用异质信念的一个十分重要的衡量指标换手率,来进行三因子模型的改进。
3.3.1. 加入换手率后的四因子模型
我们将每个月每只股票的换手率进行处理,得到每个月所有股票换手率的均值,将其作为第四个因子加入三因子模型中,代入之前的因子数据得到如下结果:

Table 7. Three-factor model parameter processing result of adding turnover rate
表7. 加入换手率的三因子模型参数处理结果

Table 8. Four-factor model fitness and p-value results for adding turnover rate
表8. 加入换手率的四因子模型拟合度以及p值结果
需要说明的是beta1、beta2、beta3和之前实证时一样依次为三个因子的系数,而beta4为换手率的系数,而常数项因为不需要对比且数据都十分接近0,故没有表出,因此之后的常数项都不进行表出。从表7中前三列的系数与原本的三因子模型实证数据相差无几,且正负都没有改变。而最后一列换手率的系数在SH、SM、BM、BL这四个投资组合中都大于0,说明在这四个组合中换手率的高低与投资组合的收益率成正比,在SL、BH中系数小于0,则在这两个组合中换手率的高低与收益率成反比。
表8中的数据和之前的结果相对比,可以看出SH、SM、SL、BH的拟合度都有轻微的提高,而BM、BL的拟合度有轻微的下降,但是总体来说是相差无几的,而且就六个组合而言,加入换手率的三因子模型整体拟合度在提高,而且p值都远远小于0.05,说明此模型效果十分显著,且四个因子的组合解释能力相对于原来的三因子增强了。
所以我们对此模型进行小部分股票的数据验证,选择的股票是BM中的平安银行和万科A两只股票,时段为2016年1月到2016年12月。要说明的是为什么不选择单只股票而是两只股票进行研究,因为市值因子的含义就是样本中的小公司收益减去样本中的大公司收益。下图1为用FF三因子模型的改进后的四因子模型以及原有的三因子模型数据拟合结果:

Figure 1. Ratio of simulated yield to actual yield
图1. 模拟收益率与实际收益率之比
从图1中我们看出模拟出来的两个收益率都高于实际收益率,而相比较而言,四因子模型的收益率更加接近实际的收益率,虽然和实际收益率的差距不小,但是也能说明四因子模型的解释能力要高于原来的三因子模型。为什么模拟出来的收益率与实际收益率相差过大呢,根据前人的相关研究,我们可以知道三因子模型是用来观测整个股市的模型,也就是说,用来检验的数据越多,则解释能力越强,模拟出来的数值就更接近实际数值,在此我们不再做此方面的数据证明,我们只是为了说明四因子模型的解释能力要稍大于三因子模型。
3.3.2. 换手率替换市值因子后的三因子模型
从前文的三因子模型数据实证中我们可以得出市场因子起的作用最大,而且没有出现与美国股市不相符的结果,所以我们选择依次将市值因子和市值比因子替换,形成新的三因子模型。
首先我们将市值因子用换手率替换,进行数据处理和回归之后得到结果:

Table 9. Three coefficients after replacing the market value factor
表9. 替换市值因子后的三个系数

Table 10. Fitness and p-value after replacement of market value factor
表10. 替换市值因子后的拟合度和p值
从表9我们可以看出市场因子仍然占主要地位,而换手率和市值比因子仍然处于次要地位,与传统三因子相比相差因子地位相同。与之前结果相同,beta1总是与所有投资组合存在正相关关系;而在SH、SM、BL中beta2大于0,在SL、BH、BM中beta2小于0,没有发现明显的规律存在;对于beta3而言,SH、SM、BH的值都大于0,而其余的三个投资组合的beta3都小于0,我们与FF三因子模型的实证结果相比较可以发现,FF三因子实证中的beta3即市值比因子的系数大于0的投资组合是SH、BH、BM,虽然和这次的结果不完全相同,但是可以看出都是包含H和M的投资组合,说明对于高价值和部分中价值的股票而言,其市值比因子系数大于0,即在考虑投资高价值和部分中价值的股票时,市值比因子总是起着正面作用,换而言之,投资者在投资此类股票时,市值比因子是个值得考虑的方面。
表10中,我们通过与表6的对比,可以看出模型的拟合度在所有投资组合中都有或多或少的下降,说明相对于换手率而言,市值因子有着更好的解释力,所以用换手率替换市值因子来改进模型看起来并没有取得预期的效果。
3.3.3. 换手率替换市值比因子后的三因子模型
用换手率替换市值比因子,结果如下:

Table 11. Three factor parameters after replacing the market value ratio factor
表11. 替换市值比因子后的三个因子参数

Table 12. Fit and p-values after changing the market value ratio factor
表12. 换市值比因子后的拟合度和p值
从表11中可以看出市场因子还是一如既往地占主导地位,而在市值比因子和换手率参数的对比中可以看出,除了SH组合以外,其余的投资组合中beta3的绝对值都要小于beta2的绝对值,即换手率的影响小于市值因子,也就是说在投资小盘股中的高价值股票时,换手率的考虑优先度要高于市值因子。再有,beta3的值在SH、SM、BM、BL中大于0,而在SL、BH中小于0,可以发现换手率在中价值股票中往往有着正面的作用,而在高价值和低价值股票中,则与其流通股数有关系,所以投资者们在投资中等价值股票时,可以关注它们的换手率。
从表12的模型拟合度与FF三因子拟合度对比之后,可以看出拟合度普遍下降,说明在这次的因子替换中,换手率相比较于市值比因子而言,它的解释能力还是不足的。
4. 结论
本文探究了资产定价理论的发展,而后对其中的FF三因子模型进行了重点研究,并应用行为金融学中的重要概念异质信念,它的其中一个重要衡量指标换手率对其进行了简单的改进,而后将FF三因子模型以及改进后模型拟合的收益率与真实收益率三者互相比较,得出以下结论:
1) FF三因子模型对中国股市确实地有着很强的解释能力,但是其中某些因子的系数正负与在美国股市的研究略有出入,说明中国股市与美国股市的实际情况不尽相同;
2) 异质信念对于收益率的预测确实有着或大或小的影响,我们选取的衡量指标换手率在与原有的三个因子组成四因子模型时,通过与实际数据的相互比对,四因子模型的解释能力略大于FF三因子模型,即加入了换手率的四因子模型更加贴合中国股市的实际情况;
3) 在换手率替换其中一个因子的改进当中,最后得到的结果并没有到达我们理想的效果,因为在替换之后,模型的解释能力反而下降了,虽然下降的幅度不大,但是也足以说明换手率相对于市值因子和市值比因子而言,它的解释能力还不足够,因此本文并没有对此改进后的模型进行数据验证;
4) 改进后得到的新模型加入了异质信念,而异质信念是行为金融学的重要概念,从理论上来说,改进的模型更贴近于实际情况。
NOTES
*通讯作者。