1. 引言
随着科学技术的发展，磁性材料在信息存储、医疗器械、生物医学等领域发挥着越来越大的作用 [1] [2] [3] [4]。磁性纳米环是一种环状纳米结构，因奇特的磁特性，受到了很多研究者的关注。研究发现：纳米环磁化过程中，在低场状态下会形成涡旋态，此时系统的杂散场接近于零，因此这一状态下的磁性纳米环可高密度集成，使系统的存储密度大幅提升 [5]。2010年，丁澜等发现SiGe纳米环的电导对外加磁场非常敏感 [6]。并解释了在外加磁场恒定的情况下，电导随曲率的关系。2015年，宁思同等利用劈裂纳米环不同部位的等离激元杂化耦合，产生了多极等离激元共振的现象。该特性非常适合于折射率传感应用，对开发新型无标记生物传感器件具有很重要的意义 [7]。2017年，缪晶晶等基于紧束缚理论，研究了石墨烯纳米环的电子结构和磁响应特性 [8]。2019年，王兆华等基于三维有限元法，发现纳米环/椭球二聚体的偏心方向和偏心率对表面等离激元共振有着重要的影响 [9]。
虽然磁性纳米环的研究广受关注，但是采用Monte Carlo方法计算纳米环磁特性的文献却比较少。其主要原因为运算时间问题：格点数量众多的纳米环在传统的Monte Carlo计算中需要耗费大量时间，从而影响了工作的效率和进度。为了解决这一问题，我们结合快速傅立叶微磁学(FFTM)方法与传统Monte Carlo方法，对不同尺寸的纳米环自旋组态形成及稳定性进行了研究。
2. 模型和算法
纳米环的主要几何参数有外半径R，内半径r，宽度w (w = R − r)。在模拟计算中，我们主要研究的对象是外半径R (20 nm ≤ R ≤ 100 nm)，内半径为r (0 nm ≤ r ≤ 80 nm)的圆环，系统的几何模型如图1。
结合磁性纳米环的特性，采用Monte Carlo方法 [5]，研究磁性纳米环的磁化动力学特性。
模拟计算中，采用有限元算法，划分单元为规则的球体单元。体系的总能量包括交换相互作用能，偶极相互作用能，磁各向异性能和塞曼能 [10]，表示为
(1)
(1)式中的参数设置与文献 [5] 一致。在模拟计算中，采用自由边界条件，模拟温度设为300 K，磁场沿着x轴正方向，而且从−2000 Oe到2000 Oe。
FFTM方法用于计算磁性系统的偶极相互作用能以及偶极相互作用场，这种方法运用了分立的卷积定理，通过计算相互作用矩阵的傅立叶变换来计算系统的偶极场，进而计算系统的偶极能 [11]。
3. 结果与讨论
图2展示的是内半径r = 20 nm，外半径不同的铁纳米环的磁滞回线。从图2可以发现，在这一条件下，不同几何形态的纳米环都存在双稳态特征：在低场区域存在“涡旋态”台阶，在高场区域存在“洋葱态”台阶 [5]。在高场区，系统的塞曼能在能量竞争中占据主导地位，外场迫使系统的自旋取向趋于外场方向，因此系统出现“洋葱态”，其对应的磁滞回线台阶即为“洋葱态”台阶 [5]。而在低场区，系统的塞满能较小，此时系统的交换能、偶极能和各向异性能占据主导地位，这几项能量相互竞争，产生“涡旋态”，其对应的磁滞回线台阶为“涡旋态”台阶 [11]。研究中还发现，“涡旋态”台阶宽度
随着外半径的增大而减小。由于台阶宽度可用于标识纳米环涡旋态的稳定性 [5]，因此从图2中可以看出，当内半径固定时，宽度越大的铁纳米环，其涡旋态越不稳定。
Figure 2. The hysteresis loops of Fe nanorings with different outer radius (r = 20 nm)
图2. 不同外半径铁纳米环的磁滞回线(r = 20 nm)
图3给出了宽度w = 50 nm，内半径不同的铁纳米环的磁滞回线。从图3可以发现，当宽度一定时，铁纳米环的内半径大小对铁纳米环系统磁化行为存在明显的影响：当内径r = 0 nm时，系统几何形态为实心圆盘，存在较大的中心能，因此系统不存在双稳态特征 [5] (如图3(a))；随着r的增大，磁滞回线逐渐出现了双稳态特征。同时，从图3中开可以看到，当r增大时，处于“洋葱态”和“涡旋态”之间过渡态逐渐减少。
为了进一步研究系统的磁化过程，我们模拟了R = 60 nm，r = 10 nm (即w = 50 nm)的铁纳米环(图3(b))的自旋组态，如图4所示。从模拟的结果看出，在不同外磁场作用下系统呈现不同的自旋组态。从图4中可以看出，当H = −2000 Oe时(图3(b)中的“1”位置)，系统出现了极化态，即“洋葱态”，如图4(a)
Figure 3. The hysteresis loops of Fe nanorings with different inner radius (w = 50 nm)
图3. w = 50 nm，不同内半径铁纳米环的磁滞回线
(a) H = −2000 Oe (b) H = 0 Oe (c) H =700 Oe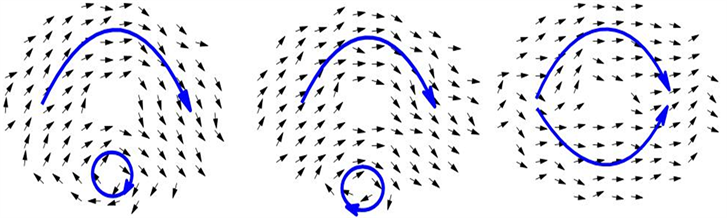
(d) H = 1100 Oe (e) H = 1300 Oe (f) H = 2000 Oe
Figure 4. Typical spin configurations of Fe nanoring (R = 60 nm, r = 10 nm)
图4. 铁纳米环典型自旋组态(R = 60 nm, r = 10 nm)
所示。随着外加正向磁场的增大，在H = 0 Oe (图3(b)中的“2”位置)时候形成“涡旋态”，继续增加正向磁场，当H = 700 Oe时，在纳米环下方出现“局部涡旋态”(如图4(c))；再增大H，我们会发现纳米环的“局部涡旋”远离纳米环中心向下运动(如图4(c)~图4(e))；当磁场增加到2000 Oe (图3(b)中的“6”位置)时，反向“洋葱态”产生，如图4(f)所示。
4. 结论
利用Monte Carlo方法结合快速傅里叶变换方法模拟了纳米环的磁特性。模拟结果表明，纳米环的内外半径会明显影响系统的磁特性。除内径为0的系统外，其他系统均出现了双稳态特征；系统在不同外场的作用下可呈现洋葱态、局部涡旋态、涡旋态和反向洋葱态等自旋组态；同时，涡旋态的稳定性与系统的内外径明显相关。本工作可为磁记录材料的实验研究提供理论依据。在下一步的工作中，我们开展大尺度纳米环阵列的模拟研究，为磁记录材料的器件设计提供相应的理论基础。
基金项目
福建省自然科学基金(2017J01553)，福建省本科高校教育教学改革研究项目(FBJG20180259)，福建师范大学本科教学改革研究项目(I201803032)，大学生创新创业训练计划项目(201910394013, cxxl-2019127, cxxl-2019s62)资助项目。
NOTES
*通讯作者。