IYPT2020下落的塔实验研究

Experimental Research of Falling Tower in IYPT2020

摘要: 对“下落的塔”的现象进行了理论分析。接着定制不同尺寸的圆盘，并将相同的圆盘叠成塔，对其底部施加一个突然的水平力以单独移除底层圆盘，若仍保持塔的稳定即为实验成功。发现了塔的稳定性与塔的层数无关，并且探究出塔的稳定性与塔的质量、金属块的直径、底层金属块和桌面的摩擦系数成正相关。该现象可应用于建筑底部放置球体的制震结构。

Abstract: The phenomenon of the “Falling Tower” was analyzed theoretically. Then different sizes of discs were prepared. Identical discs are stacked one on top of another to form a freestanding tower, and the bottom disc can be removed by applying a sudden horizontal force. If the tower remains stable, the experiment will be proved successfully. The results show that the stability of tower has no connection with the number of layers, but is positively related to the mass of tower, the diameter of disc and the frictional coefficient of platform. The phenomenon can be applied to earthquake-resistant structures with spheres placed on the bottom of the building.

1. 引言

砖块搭建的层状建筑或者若干个物块的层叠堆积物放置在地面，当底层的物块受到外部水平力的作用时，物块之间会发生相互作用，它们最终的运动状态与物块之间的摩擦系数、外力大小和底部物块与地面之间的摩擦系数都有关系。本文定量研究该问题，对于建筑的稳定性设计具有一定的理论参考价值。

2. 实验原理

国际青年物理学家学术研究锦标赛简称IYPT，本文的课题来自于IYPT。如图1所示，把几块相同的圆盘上下整齐地叠放在一起，构成下落的塔。在圆盘没有分离前，我们可以把圆盘的运动分解成两部分：第一阶段是在底层圆盘与上层的整体进行水平相对位移。我们可以通过牛顿运动定律进行分析。而第二阶段是上层圆盘倾斜，发生刚体转动。我们可以通过刚体力学进行分析。我们假设在圆盘的运动过程中受到的空气阻力的为零，对“下落的塔”的稳定性进行分析。

2.1. 牛顿力学分析

(1) 我们首先假设出一个由四个质量为m的尺寸、粗糙度完全相同的圆盘组成的“下落的塔”，如图1所示。

Figure 1. The tower made of disks of the same mass

图1. 质量相同圆盘所堆的“塔”

(2) 当底层圆盘1受到一个外力时，系统受力如图2所示 [1]。

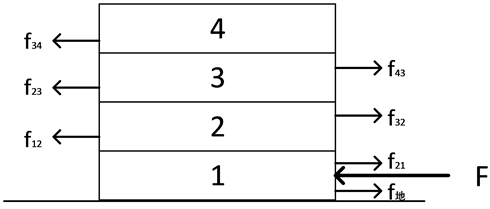
Figure 2. The subjected force diagram of tower

图2. “塔”的系统受力图

分析系统受力：

$F-3mg{\mu }_{物}-4mg{\mu }_{地}=m{a}_1$ (1)

$3mg{\mu }_{物}-2mg{\mu }_{物}=m{a}_2$ (2)

$2mg{\mu }_{物}-mg{\mu }_{物}=m{a}_3$ (3)

$mg{\mu }_{物}=m{a}_4$ (4)

因此时底层滑出，顶层三个圆盘相对静止，根据

$a_1>a_2=a_3=a_4$ (5)

得：

2.2. 刚体力学分析

(1) 从顶层圆盘2、3、4开始倾斜，直到与圆盘1分离可视为阶段2，如图3所示。

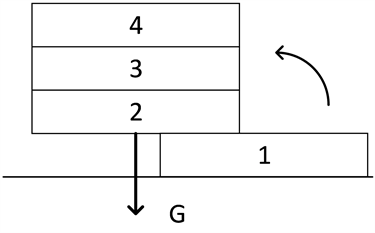
Figure 3. The disks tilt away from the center of gravity

图3. 圆盘偏离重心发生倾斜

(2) 取1、2单独分析，设圆盘的角加速度为 $\alpha$，圆盘中心到倾斜点的距离为r，圆盘的直径为d，高度为h，转过的倾角为φ。刚体力学分析如图4所示。

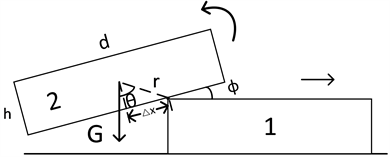
Figure 4. The analysis of separated disks of number 1 and 2

图4. 取1、2单独分析

根据刚体力学公式 [2]：

$r\times F=J\cdot \alpha$ (6)

带入数据得：

$\sqrt{{\left(\frac{h}{2}\right)}^2+\Delta x^2}\cdot \left(mg\sin \theta \right)=J\cdot \frac{{\text{d}}^2\phi }{\text{d}{t}^2}$

$\theta =\arctan \left(\frac{\Delta x}{\frac{d}{2}}\right)+\phi$

计算转动惯量：

$J=\frac{1}{3}m\left[{\left(\frac{h}{2}\right)}^2+{\left(\frac{d}{2}\right)}^2\right]+m\left[{\left(\frac{h}{2}\right)}^2+\Delta x^2\right]$ (7)

可得关系式如下：

$\sqrt{{\left(\frac{h}{2}\right)}^2+\Delta x^2}\cdot \left(mg\sin \theta \right)=\left[\frac{1}{3}m\left(h^2+{\left(\frac{d}{2}\right)}^2+3\Delta x^2\right)\right]\cdot \frac{{\text{d}}^2\phi }{\text{d}{t}^2}$ (8)

根据上文的分析我们不难发现，在第一阶段，底层圆盘1的滑动取决于圆盘的质量、桌面和圆盘1之间摩擦系数、圆盘1和圆盘2之间的摩擦系数以及所施加外力的关系。在第二阶段，顶层圆盘2、3、4整体的倾斜则与圆盘的直径和高度有关。接下来的实验也主要以上述的因素作为研究对象。

3. 实验装置及实验方法

实验装置有：电子天平，定滑轮，轻绳，物品袋，不同直径、高度、粗糙度的304不锈钢金属块(ϕ 40*8 mm酸白、ϕ 40*8 mm抛光、ϕ 40*8 mm磨砂、ϕ 20*8 mm酸白、ϕ 30*8 mm酸白、ϕ 50*8 mm酸白、ϕ 40*4 mm酸白、ϕ 40*16 mm酸白)。

实验步骤如下。

3.1. 准备实验器材

(1) 根据实验目的以及实验原理，定制出不同直径、高度、粗糙度的304不锈钢金属块。

(2) 通过电子天平测量不同规格的不锈钢金属块和物品袋的质量。

(3) 取出适量的被同规格的金属块作为砝码。

3.2. 根据实验原理进行实验，测量数据并记录

(1) 将轻绳的一端连上物品袋，穿过定滑轮，另一端系上圆环结。

(2) 将2个ϕ 40*8的金属块叠加在离定滑轮35 cm的桌面上，并在最底层金属块上套好圆环结，向物品袋中加入一个ϕ 40*8作为砝码，观察是否成功完成“下落的塔”。

(3) 重复以上步骤10次，若成功与失败的次数相差过大，则选择次数较多的现象并记录；若成功和失败的次数接近，则进行标记，并选择其他质量的金属块作为砝码，并记录实验刚好成功时的砝码的重量。

(4) 若成功完成“下落的塔”，则在金属块上再叠加一个金属块，并重复步骤；若没有完成，则在物品袋里加入一个砝码，重复步骤(3)中的操作。

(5) 根据不同的研究对象，分别选取不同规格的金属块，重复步骤(2)、步骤(3)、步骤(4)中的操作。

注意事项：

(1) 在实验前选择合适的安全距离，防止金属块损坏定滑轮。

(2) 尽量让轻绳与桌面水平。

(3) 待绳子自然伸直后，平稳释放重物。

(4) 每组实验重复进行，临界点附近密集取值。

4. 测量结果分析

由于器材的限制，本次实验将主要从牛顿力学所分析的影响因素入手。为了使实验结果更加直观，我们将不同规格的金属块尺寸在实验刚好成功时砝码的重力即临界点的水平作用力和“塔”的层数做出了如下的关系图。

4.1. 金属块直径

通过对比尺寸分别为ϕ 20*8、ϕ 30*8、ϕ 40*8、ϕ 50*8的金属块的临界作用力与层数的关系图(图5)，我们发现：临界水平力与金属块直径正相关，即其他条件相同时，金属块的直径越大，稳定性越高。联系上文的分析，金属块的直径的改变也导致了塔身的质量发生改变，进而影响其稳定状态。因此我们也验证了塔的质量与“下落的塔”稳定性的关系。

Figure 5. Diagram of relationship between critical horizontal force and number of layers of metal blocks with different diameters

图5. 不同直径金属块临界水平力–层数关系图

4.2. 金属块粗糙度

由于材料的限制，我们无法选择粗糙度成定值的金属块。但通过对比粗糙度明显不同的抛光面、酸白面、磨砂面的金属块的临界作用力与层数的关系图(图6)，我们可以发现：临界水平力与金属块的粗糙度正相关，即其他条件相同时，金属块的粗糙程度越大，稳定性越高。这也验证了上文中的分析——塔的稳定性与金属块之间的摩擦因数有关。

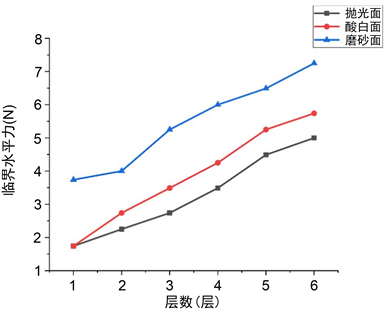
Figure 6. Diagram of relationship between critical horizontal force and number of layers of metal blocks with different roughness

图6. 不同粗糙度金属块临界水平力–层数关系图

4.3. 金属块的层数

通过研究发现，塔的稳定性与金属块的质量有关。为了使该研究不受金属块质量的影响。我们选取高度成倍数的金属块：ϕ 40*4、ϕ 40*8、ϕ 40*16，将ϕ 40*16层数为1时的作用力与ϕ 40*8层数为2时的作用力以及ϕ 40*4层数为4时的作用力进行对比。这样既改变了塔的层数，又使金属块的质量保持不变。下图为临界水平力与ϕ 40*8金属块的层数的关系图，如图7。(注：ϕ 40*4、ϕ 40*16的层数分别扩大、缩小一倍)，我们发现：三种尺寸的金属块曲线基本重合。根据上文的分析，当金属块没有分离之前，可看做一个整体，因此，当仅改变塔的层数时，不会影响塔的稳定性。

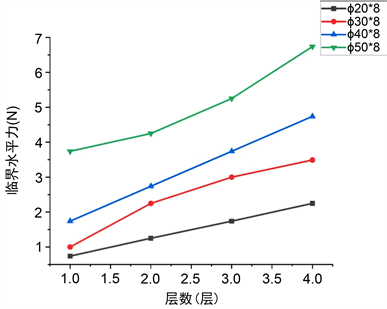
Figure 7. Diagram of relationship between critical horizontal force and number of layers of metal block with different heights

图7. 不同高度金属块临界水平力–层数关系图

5. 结语

本实验测试了“下落的塔”，不但发现了塔的稳定性与塔的层数无关，而且探究出与塔的质量、金属块的直径、与底层金属块和桌面的摩擦系数成正相关之间的关系。除此之外，理论分析发现塔能否保持静止直立与其重心也有关系，如果要单独考虑重心问题，则需不同材质的圆盘，因材料限制未能深入探究。

该发现可以应用于建筑的制震结构：地震中的横波相当于突然的水平力，通过减小建筑与底层装置的摩擦系数，例如在建筑物中放置各种球体，让其吸收地震能量，确保建筑其他地方不会发生问题，达到防震减灾的目的 [3] [4]。

基金项目

上海市大学生科技创新项目《磁场中冷热探针测量硅片的载流子浓度实验研究》。

NOTES

^*通讯作者。