1. 引言
惯性导航系统(Inertial Navigation System)在启动时,必须依赖提供的外部精准信息完成初始对准,以修正惯性系统惯性平台的初始失调角。由于使用惯性导航系统的运载平台的差异,其采用的初始对准方式也不一样,如机载平台通常采用“传递对准”方式、陆用平台则“行进间”对准方式较为普遍、船载平台以码头条件的“系泊对准”为主要考虑的对准方式;同时由于惯导设备形态的差别,采用的对准方式也不尽相同,如捷联惯导系统主要采用凝固坐标系 + 卡尔曼滤波器的方式完成初始对准、液浮惯导则采用传统的经典控制网络实现初始对准。本文讨论的是空间稳定型惯导系统,采用H∞ control的方式实现初始对准。
空间稳定型惯导系统平台框架结构如图1所示,由于陀螺和加速度计装于惯性平台,一起稳定于地心惯性坐标系,相对于当地重力矢量翻滚 [1]。加速度计输出含有重力分量,为了得到地理坐标系中水平面内的加速度,必须精确分辨出重力分量。所以对空间稳定惯性导航系统的加速度计标度因数非线性、标度因数稳定性及零偏提出了很高要求,如果加速度计的动态特性稍差,必然在加表信号输入中带入干扰。同时由于静电支撑陀螺壳体连续旋转,虽然调制了其陀螺本身常值漂移,但是因为壳体翻滚轴或台体翻滚轴不可能与陀螺动量矩矢量一致,即存在壳体翻滚或台体翻滚失准角,也给惯性导航系统带来附加的误差 [2]。在考虑动态情况下,加速度计、陀螺壳体旋转、框架的随动跟踪误差等因素,造成了在初始对准过程中对准时间长,对准精度不高。考虑到H∞控制技术对于噪声不敏感性和鲁棒性,本文将H∞控制的设计方法,运用于空间稳定型惯导系统的初始对准中。研究表明,该方法能有效抑制不确定性干扰的影响,对于提高空间稳定惯性导航系统的动态对准性能效果明显。
2. H∞控制技术
以连续定常系统为例,其动态方程作为广义控制对象:
(1)
其中,
为外输入信号,包括外干扰、噪声、参考输入等;
为控制信号;
为被控输出信号;
为被测信号。
代表广义被控对象,
代表要设计的控制器。
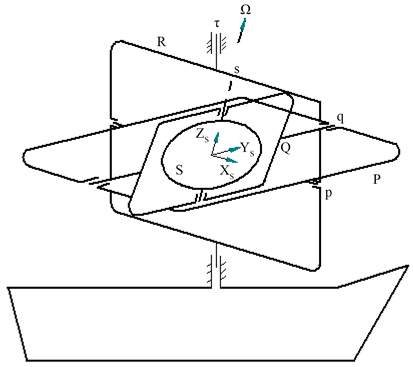
Figure 1. The frame structure of space-stable system
图1. 空间稳定系统框架结构示意图
在确定性次优滤波过程中,可将噪声看作是能量有限的随机信号,使系统的干扰到估计误差的闭环传递函数的范数小于给定的正数 [3]。
若相应的传递函数形式为
(2)
则从
到z的闭环传递函数为
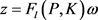 (3)
(3)
其中,
。最优
控制的目的就是设计控制器
使闭环系统内稳定且使系统闭环传递函数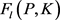 的无穷范数极小。由于寻找
最优控制器在数值计算和理论上都很复杂,且在实际应用中往往没有必要,因此通常设计的控制器是在范数意义上接近最优控制器的次优控制器,即满足
的无穷范数极小。由于寻找
最优控制器在数值计算和理论上都很复杂,且在实际应用中往往没有必要,因此通常设计的控制器是在范数意义上接近最优控制器的次优控制器,即满足
(4)
其中
为给定常数。
3. 空间稳定型惯导系统初始对准的H∞应用
3.1. 初始对准步骤
空间稳定惯性导航系统原理如图2所示,其初始对准分为两个步骤进行,第一个步骤为粗对准(平台对准),在陀螺启动之前,借助外部信息(如平台罗经提供的姿态信息)平台用平衡环锁定技术(将指令角度输入平衡环模数转换器)定向,调整框架使平台坐标系与惯性坐标系接近一致。第二个步骤为精对准(确定平台坐标系的实际指向),即确定平台坐标系相对于惯性坐标系的关系或者确定平台坐标系相对于当地地理坐标系的关系 [4]。这个过程采用自校准法通过经典的校准网络,以地球转速
、
为基准信号由惯导计算机完成精对准。这一过程即为“数学平台”的调平过程。
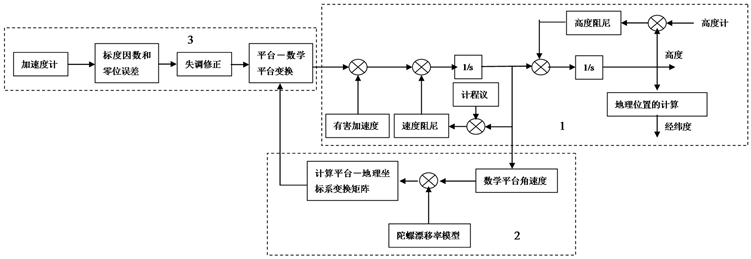
Figure 2. The space-stable inertial navigation system
图2. 空间稳定惯性导航系统
3.2. 精对准实现
空间稳定型惯导系统精对准中根据在不同坐标标系的编排可以考虑在惯性坐标系下和地理坐标系下实现。但在惯性坐标系的机械编排中,平台坐标系引出的加速度讯号直接在地心惯性坐标系中解算,由于重力分量的补偿比较困难,难以寻找一个基准信号(地理坐标系下的基准信号为
)作为参考在这样的情况下设计初始对准网络不容易满足其导航要求的对准精度,因此考虑在地理坐标系编排中实现精对准,如图3所示。
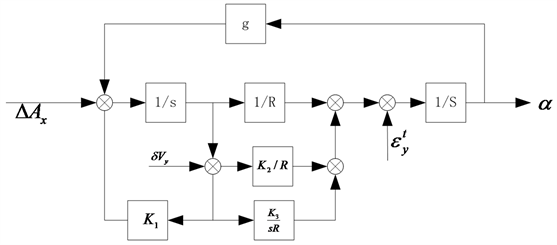
Figure 3. The error block diagram of horizontal circuit in north direction
图3. 北向水平回路误差方块图
3.3. “数学平台”解算
a)
的变化计算
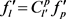 (5)
(5)
式中
:平台坐标系加速度计输出;
 :平台坐标系向地理坐标系转换;
:平台坐标系向地理坐标系转换;
b) 有害加速度计算
(6)
其中“
”表示解算量。
c)
的解算方程
(7)
式中
(8)
D方程满足以下方程:
(9)
J方程由下式计算
(10)
d) 角速度
的计算
(11)
e)
的求解
满足方程
(12)
此时,用解算的速度计算“数学平台”相对于惯性空间的角速度,不断求解变换矩阵
,使得速度误差逐渐趋于零这个过程,也就是
趋于
的过程。在这个过程中,重力分量的调节过程如图4所示。精对准的调整过程就是不断使
趋于
的过程,当调整结束时认为已经精确的确定了矩阵
,相当于“数学平台”已经得到了对准 [5]。同时也就确定了平台坐标系的精确指向。
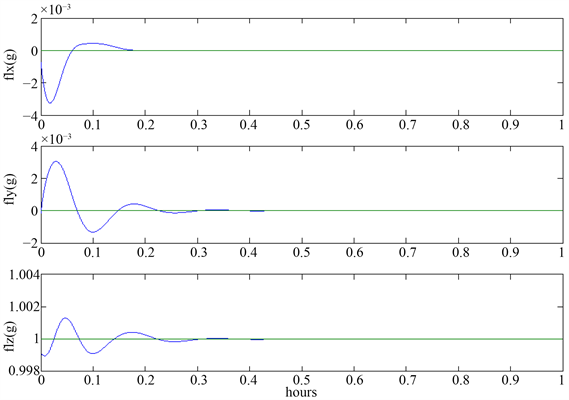
Figure 4. The gravity change process in initial alignment
图4. 初始对准中重力分量变化过程
3.4. H∞控制的初始对准
如果考虑到系统的干扰如陀螺壳体旋转、加速度计的非线性、框架随动的跟踪误差等因素。系统的初始对准将无法达到2.3节中所述效果,故采用H∞控制技术设计初始对准。同经典分析方法类似,把水平对准和方位对准分开来考虑。以水平回路为例讨论,系统的方块如图5所示。
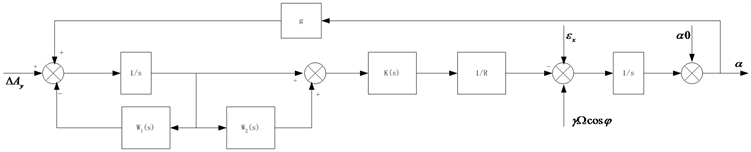
Figure 5. The block diagram in horizontal alignment
图5. 水平对准方块图
(13)
在空间稳定惯性导航中,系统加速度计零偏为常值时造成的“数学平台”误差角如式(13)所述。如果考虑系统中壳体旋转造成的影响为
,框架跟踪误差和加速度计的非线性综合考虑为
为一高频有界不确定量 [6],
,频率
。最终体现在加速度计上的误差为:
(14)
在基于混合灵敏度的
控制方法要求
(15)
其中
为系统的灵敏度函数, 为补灵敏度函数。考虑到加权函数
和
,系统的增广状态方程可化为标准
控制方程 [7] [8],其中
为补灵敏度函数。考虑到加权函数
和
,系统的增广状态方程可化为标准
控制方程 [7] [8],其中
;
;
;
;
;
;
;
;
.
利用
控制理论,可求得一近似最优控制器:
(16)
当方位回路设计时与水平回路相似,
(17)
仿真比较
控制技术设计的初始对准与传统的初始对准,设陀螺常值漂移:
;陀螺与g有关项漂移系数:
;陀螺与g2有关项漂移系数:
;加速度计零位:
;壳体的旋转干扰:
,
,
;壳体旋转、框架随动等干扰:
,
;平台粗对准后初始不对准角:
。

Figure 6. The comparison of two initial alignment schemes
图6. 两种初始对准方案比较
图6可以看出,在带有干扰的空间稳定型惯导系统初始动态对准中,H∞控制方案与经典控制方案相比,具有两个突出优点:一方面它缩短了对准时间,H∞控制方案在100分钟左右就已经进入了稳态,而经典的控制收敛的效果与H∞控制方案相比,在精度上较差;同时在外界干扰噪声较大的情况下,H∞控制方案方位对准后的波动更小,体现了系统具有较强的鲁棒性。
4. 结论
本文针对空间稳定型惯性导航系统的特点,开展其初始对准的研究。在系统分析和设计阶段,充分考虑被控对象所存在的不确定因素,如空间稳定型惯导系统各框架的“牵连”干涉运动,对精确初始对准带来的影响,因此利用H∞控制技术设计了近似最优控制器,给出了保持系统渐进稳定且满足给定H∞性能指标的充分条件,针对空间稳定型的对准方式,引入了加权函数进行自适应调节,根据空间稳定型惯性导航系统的误差规律,得到了可用于控制输入的未知时滞参数的自适应律。通过仿真实验,验证了H∞控制技术克服系统噪声的不确定等因素的有效性,提升了10%的初始对准精度,同时能够一定程度缩短约系统初始对准时间。
基金项目
国家科技部重大仪器专项(2013YQ310799)。