1. 引言
核电厂中安全壳的作用是在正常运行和事故工况下,包容放射性物质,从而保证周围公众和环境的安全。然而,在核电厂发生事故期间,即使安全壳没有严重失效或破坏,放射性裂变产物气溶胶仍然会通过安全壳内可能存在的微小通道泄漏到外界环境中去。这些安全壳内可能存在的微小通道包括安全壳的裂缝、某些老化的密封件或贯穿件、波纹管和焊缝等。
目前,许多国家在进行反应堆的安全分析以及评估核事故条件下释放到环境中的源项时,仍然把气溶胶粒子从这些微小通道的泄漏速率按和普通气体一样进行计算,完全忽略气溶胶在这些微小通道的沉积和滞留效应 [1]。然而,大量的实验研究 [1] 表明,气溶胶粒子在通过这些微小通道时,会在多种沉积机制的作用下,在微小通道内发生沉积,且这些沉积的气溶胶粒子还可能堵塞这些微小通道 [1],从而显著减少放射性气溶胶向环境的泄漏。如Watanabe [2] 对典型沸水堆安全壳的试验研究表明,如果考虑气溶胶粒子在微小通道内的滞留和堵塞效应,事故1天后泄漏到环境中的裂变产物总量减少了约50%~70%。
至少从10CFR 100建立以来,放射性气溶胶在这些微小通道内的泄漏和滞留就成为反应堆安全分析的关注点 [1]。通过对气溶胶粒子在微通道内沉积效应的研究,可以进一步提高对释放到环境中的源项进行评估的技术水平。
本文选取了部分代表性的微通道内气溶胶沉积模型进行介绍。本文的研究成果将为安全壳微小通道内气溶胶沉积模型的研究奠定基础。
2. 微小通道内气溶胶沉积机制介绍
可能导致气溶胶粒子在微小通道内发生沉积的沉积机制很多,大体如下:
1) 重力沉降
气溶胶粒子为具有一定体积和质量的实体颗粒,则其在重力作用下,会在微小通道内发生沉积,这种沉积机制称为重力沉降。实验研究 [1] 和模型研究 [3] 均表明,当流速相对较低时,重力沉降对尺寸较大的气溶胶粒子影响更大。此外,重力沉降与微小通道的布置有关,如果微小通道垂直布置,则重力沉降对气溶胶粒子在微小通道内的沉积不起作用。
2) 布朗扩散
气溶胶粒子会在布朗扩散的作用下,在微小通道内发生沉积,该沉积机制称为布朗扩散。现有研究表明 [3],在层流状态下,布朗扩散对尺寸较小的气溶胶粒子影响较大。
3) 扩散泳
当蒸汽在微小通道壁面发生凝结时,靠近微小通道壁面处的蒸汽浓度较低,而远离微小通道壁面处蒸汽的浓度较高,该蒸汽浓度梯度的存在会引起分子扩散,进而能够导致气溶胶粒子的运动,该运动既包含存在非冷凝成分引起的流体动力流,也包含了扩散泳力驱动的流体运动 [4]。气溶胶粒子在上述运动过程中,向壁面运动,进而在壁面上发生沉积,这种沉积机制称为扩散泳。
4) 蒸汽凝结
当气溶胶的载体气体中存在水蒸气时,气溶胶粒子可能在蒸汽凝结的作用下发生沉积。蒸汽凝结的作用机制有两种 [5],第一种,当蒸汽与微小通道壁面之间存在温度梯度时,蒸气就会在微小通道壁面上发生凝结。随着蒸汽在壁面上的凝结,会加强气溶胶粒子的扩散泳去除;第二种,当蒸气与气溶胶粒子之间存在温度梯度时,蒸汽也可能在气溶胶粒子表面发生凝结,此时将增加气溶胶粒子的重力沉降速率。
5) 热泳
当通道内存在温度梯度时,在其内流动的气溶胶粒子会受到一个沿温度降低方向的力,即热泳力。热泳力的大小与温度梯度成正比。在热泳力的作用下,气溶胶粒子由高温区域向低温区域运动的现象叫做热泳 [4]。现有模型研究结果表明 [3],在层流状态下,热泳对小尺寸的气溶胶粒子有较大影响。
6) 电泳
在有些情况下,气溶胶粒子可能带有电荷。当存在电场时,会驱动气溶胶粒子沿着一个固定方向运动,气溶胶粒子在此作用下发生沉积的机制称为电泳 [4]。
7) 惯性碰撞
由于气溶胶粒子具有一定的体积和质量,则其在运动过程中可能会脱离流线,与微小通道壁面发生碰撞,称为惯性碰撞。气溶胶粒子尺寸在5~10 μm之间时容易受到惯性碰撞的影响 [6]。通常而言,当气溶胶粒子进入微小通道时,会在入口处与壁面发生惯性碰撞,造成一部分气溶胶粒子的损失;此外,在通道内输运过程中,气溶胶粒子也会与内壁面发生惯性碰撞。这两种惯性碰撞需要分开考虑,总的气溶胶粒子惯性碰撞损失是二者的综合结果。
8) 湍流扩散
当流体处于湍流流动状态时,存在着一系列大小和强度不等的漩涡,这些漩涡基本以随机的方式向流体的各个方向移动。部分气溶胶粒子会进入这些漩涡中,并随着漩涡一起运动,该现象称为湍流扩散。
9) 涡流碰撞
当流体处于湍流流动状态时,如果气溶胶粒子的惯性力较小,它们通常会在通道的后端由于涡流的作用而发生聚集沉积,该沉积过程称为涡流碰撞。涡流碰撞作用的气溶胶粒子尺寸通常在1~10 μm之间,以及那些易受扩散和热泳影响的气溶胶粒子 [6]。
10) 平流夹带
通道内气体的流动可能导致气溶胶粒子被夹带,由此导致的气溶胶粒子在微小通道内的沉积称为平流夹带 [4]。
11) 反弹
沉积到通道表面的气溶胶粒子不会永远都停留在通道表面上,而是可能通过与表面的反弹而重新返回到流体中 [1]。
12) 再悬浮
再悬浮也是沉积到通道表面的气溶胶粒子再次回到流体中的一种方式。可能引发气溶胶粒子再悬浮的机理有很多种 [1],如沉积粒子上方的气流突然转变方向,这种机理引发的再悬浮的特点是会有一个突然大的再悬浮现象,之后伴随着长期的、短暂的、小的再悬浮现象。新沉积的气溶胶粒子更容易受此机理的影响,发生再悬浮;粒子的影响也是诱发再悬浮的机理之一。
13) 静电沉积
气溶胶粒子可能由于空气中存在的自由离子、天然放射性及粒子间的相互摩擦碰撞而带电,从而发生静电沉积 [7]。
3. 多沉积机制及堵塞模型
3.1. M-V模型
Morewitz和Vaughan [1] 提出了一个非常简单的模型来预计通道在发生完全堵塞之前通过的气溶胶质量,其数学表达式如下式(1)所示:
(1)
其中,
为通道在发生完全堵塞之前通过的气溶胶质量,kg;
为由实验数据拟合的经验常数 = (5 ± 3) × 104,kg/m3;
为泄漏通道的等效水力直径,m。
M-V模型的提出迅速引起了气溶胶协会的关注和讨论。该协会认为反应堆安全分析中关注的微小泄漏通道气溶胶滞留行为和从大气中气溶胶样品的取样问题是类似的。基于气溶胶粒子的斯托克斯数(Stk)及重力沉降速度,Davies、Agarwal和Liu分别提出了取样准则 [1],以保证按此准则取得的样本能够代表总体的真实情况。仅当不满足上述取样准则时,M-V模型才是适用的。因此,总体来看,M-V模型的适用范围较小,且由于该模型没有考虑气溶胶粒子在通道内的各种沉积机制,也是该模型的一大缺陷 [1]。
3.2. Williams模型
Williams模型 [4] 在分析气溶胶粒子在微小通道内的沉积时,综合了气溶胶粒子的各种沉积机理的计算,并考虑了堵塞物的形成,通过一系列假设,给出了沉积方程的解析解。Williams在分析计算时划分了以下三个步骤:
步骤1:计算通过非均匀截面通道的气体流量;
步骤2:计算气流中的气溶胶粒子通过各种沉积机制沉降到壁面的沉积量;
步骤3:确定通道堵塞的形成速度和时间。
在上述三个步骤的分析计算中,需要考虑以下问题:
a) 由于流道几何形状的不确定性以及流体本身温度、压力、组成成分等的差异,将气流的流动分为层流流动和湍流流动分别研究。在计算时也考虑了弯头的影响以及通道内表面粗糙度的影响。
b) 对气溶胶粒子在通道表面的沉积速率进行计算,在计算时考虑了如下沉积机理:重力沉降、布朗扩散、热泳、扩散泳、湍流扩散、电泳、平流夹带、惯性碰撞(通道内)。沉积速率与气流的流型、气溶胶粒子的大小、粒子的质量及通道表面的粗糙度有关。
c) 由于气溶胶粒子在通道内的沉积(也可能有气溶胶粒子的再悬浮过程发生),会使通道的流通面积变小,流道的几何形状不断发生改变,进而又会影响到流型。也就是说a)、b)、c)之间是相互关联的,需要处理好变量之间的耦合关系。
d) 建立通道堵塞的数学模型,给出近似的解析解,从而评估气溶胶粒子通过通道进入大气的量。
Williams模型经过一系列的简化处理,这导致该模型理论存在一些不足之处,如,始终将流动当作湍流流动、对堵塞物的形状轮廓进行了具体的假设、忽略了通道入口附近的惯性碰撞等。此外,虽然Williams模型在建立过程中已经进行了很多简化和近似,但模型仍然十分复杂。
3.3. Gelain模型
Gelain模型 [8] 描述了气溶胶通过混凝土裂缝的沉积份额。为了对流体在混凝土裂缝中的行为进行建模,模型中采用如图1所示的简化模型来表示混凝土裂缝的网络结构。该简化模型将混凝土裂缝简化为一个长“L”,宽“e”,范围跨度为“l”的矩形通道。该混凝土裂缝的简化近似模型同时被众多的研究者所采纳 [1] [8]。因此,Gelain模型的第一步便需要确定混凝土裂缝的上述三个特征量;在此基础上,可进一步评估在层流状态下气溶胶粒子的沉积份额。
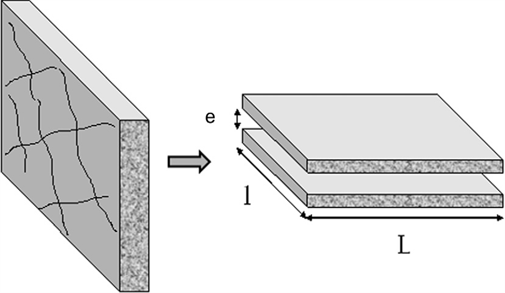
Figure 1. The simple model for containment crack used in Gelain model
图1. Gelain模型中采用的简化混凝土裂缝模型
Gelain模型中采用的实验样本代表了钢筋混凝土墙体受到地震剪切应力作用后形成的裂缝。为确定混凝土裂缝的特征尺寸,需要三类方程,将上述三个特征尺寸关联起来,具体如下:
方程1:裂缝宽度“e”和范围跨度“l”的关联方程;
方程2:裂缝长度“L”的计算方程;
方程3:裂缝三个特征量的关联方程。
Gelain模型中考虑了三种类型的气溶胶沉积机制,分别为:布朗扩散、重力沉降和惯性碰撞(入口处),而气溶胶粒子的沉积采用沉积份额的形式表示,总的沉积份额如下式(2)所示:
 (2)
(2)
其中,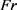 为总沉积份额,无量纲;
为总沉积份额,无量纲; 为各沉积机制导致的沉积份额,无量纲。
为各沉积机制导致的沉积份额,无量纲。
Gelain模型中给出的气溶胶粒子沉积模型仅在气溶胶处于层流流动状态及干燥的环境中进行了验证,其对其他情况的适用性还有待进一步检验。
3.4. Demokritos模型
为了完善ASTEC程序,使其更好地评估严重事故源项,希腊的Demokritos研究中心开发了新的数值模型来研究气溶胶粒子在微通道(缝隙)内的沉积以及堵塞的形成 [9]。Demokritos模型以一维气溶胶输运方程的数值解为基础,结合了多种气溶胶沉积机制,根据沉积的气溶胶粒子质量来确定通道(缝隙)面积随时间的变化。
Demokritos模型中将通道(缝隙)假定为一个直的通道,并保守地忽略通道壁面的粗糙度。在气溶胶流动模型中只考虑了输运、沉积等外部过程,内部气溶胶粒子之间反应等内部过程没有考虑。Demokritos模型中共考虑了四种气溶胶粒子的沉积机制:重力沉降、布朗扩散、湍流扩散和涡流碰撞,并将其按照流体的流态进一步细化,当流体处于层流流动状态时,仅考虑重力沉降和布朗扩散;而当流体处于湍流流动状态时,忽略布朗扩散的作用。
Demokritos模型相对简单,便于建立数值算法,能够对微通道内气溶胶的堵塞与滞留做出较为合理的估计;从反应堆安全角度来看,尽管该模型的计算结果相对保守,但仍然可以应用于像ASTEC等大型严重事故分析程序中,改善目前安全分析程序不能分析放射性气溶胶在安全壳缝隙中的滞留与堵塞的现状,修正严重事故下释放到环境中的源项。当然,该模型也存在一些不足有待完善,比如对微通道形状的考虑不够全面,对气溶胶粒子在通道入口的碰撞损失估计不足等。
3.5. 小结
将上述介绍的多沉积机制及堵塞模型进行横向比较,可知:
1) 仅M-V模型没有考虑流体的水力学特征和气溶胶粒子在通道内的各种沉积机制;
2) Gelain模型适用于流体处于层流流态,而Demokritos模型、Williams模型既适用于流体处于层流流态,也适用于流体处于湍流流态;
3) Williams模型考虑的气溶胶粒子沉积机制最全面;
4) Demokritos模型相对简单,便于建立数值解法,同时该模型的预测结果无论与Williams模型还是与大部分实验的结果吻合都较好;
5) Demokritos模型中对部分参数的选择没有给出详细的指导。这些参数的选取原则可部分地参考其他模型,如Williams模型;
6) 上述任一模型均没有考虑静电沉积、蒸汽凝结、反弹和再悬浮的气溶胶粒子沉积机制。
4. 总结与建议
本文对安全壳微小通道内气溶胶粒子的沉积模型进行了充分的调研,结合本文调研结果可知:
1) 现有的考虑多种沉积机制的模型,或多或少存在一些不足之处,如Williams模型在求解过程中进行了大量的假设和近似,而Demokritos模型考虑的沉积机制相对较少;
2) 在研究气溶胶在微小通道内的沉积效应时,应重点考虑如下影响因素:
a) 热工水力因素:安全壳内的压力、安全壳内气体的组成、沿安全壳微小通道的压降以及壁面温度、气溶胶粒子在微小通道内表面的蒸汽凝结;
b) 安全壳微小通道几何形状:微小通道的路径和水力直径、沉积气溶胶的形状及其变化;
c) 气溶胶特征:安全壳内气溶胶的组成、浓度、尺寸分布。
3) 目前的模型普遍忽略了蒸汽凝结对气溶胶沉积的影响,但在严重事故工况下,尤其是轻水反应堆,载体气体中水蒸气的含量可能很高,后续可以在这方面继续完善。
致谢
特别感谢上海核工程研究设计院的同事高圣钦工程师对本工作所做的前期筹备工作。
基金项目
本研究由国家科技重大专项《大型先进压水堆及高温气冷堆核电站》子课题“压水堆安全壳气溶胶微小通道泄漏与滞留研究”(2019ZX06004013)资助。