1. 引言
在无向图G = (V, E)中,团(clique)指图G的一个完全子图,完全子图是指在图内节点之间均有边相连。最大团问题旨在给定的图G中找出一个或若干个团,团内所包含的节点数是最多的。最大团问题在生物信息学、编码理论、计算机视觉、组合拍卖、经济学分析、社会网络分析等实际问题中,存在着广泛的应用,与最大独立集、最小顶点覆盖、图染色等其他经典的NP难度问题也密切相关。
在已有求解最大团问题的算法中,根据求解方式及结果精确度的不同主要被分为两种:精确性算法和启发式算法。启发式算法是以牺牲准确性来达到提高求解速度的目的,而精确性算法采用对所有可能解进行保留的方法,从而保证了所求解为全局最优。虽然在理论的角度上分析,对所有可能解进行保留验证对比的方法使得精确性算法在时间复杂度上居高不下,但近年来的研究进步使得精确性算法的实际求解能力得到显著提升。
本文研究基于邻接点的最大团精确性算法。论文紧紧围绕最大团中两两节点间均有边相连的性质展开,具体组织结构如下:第二部分介绍关于求解最大团的研究现状:接着对最大团问题相关概念进行介绍,并由最大团的性质提出一种求解最大团问题的算法及并进行算法示例;然后证明基于邻接点求解最大团问题的算法具有正确性及完整性;并利用本文所提出的基于邻接点求解最大团的方法实际应用于求包含任意节点的最大团;最后总结全文并阐述未来工作。
2. 研究现状
求解最大团问题在多项式时间内可以转化为其他问题,然而,由于任意图上的最大团问题是一个单项式时间算法,现有的多项式算法主要集中在一些特殊图上——如处处h可断图 [1]、循环图 [2] [3]、无爪图 [4] 等。
现有的求解最大团问题的算法主要分为两种:精确性算法和启发式算法。最初提出求解最大团问题时,研究人员的主要研究方向为精确性算法,最早的精确性算法(Exact algorithm)——枚举法于1957年由Hararv和Ross提出 [5],随后1981年,Tsouros [6] 引进深度优先来解决时间复杂度太高的问题,结果证明取得了一定的效果,而后来又基于枚举法提出了分支定界法,分支定界法明确只求得图中的最大团,避免产生冗余的候选最大团,因此采用分支定界法求解最大团的关键在于找到较好的上界、下界以及确定的分支策略,在很大程度上改善了算法的时间复杂度以及空间质量。
随着对最大团问题研究的深入以及图规模的增长,精确性算法因其求解时间长效率低,启发式算法凭借其能够在较短的时间里得到近似解获得研究学者们的青睐,经典的启发式算法包括:蚂蚁算法 [7]、遗传算法 [8]、神经网络 [9]、模拟退火 [10] 和禁忌搜索 [11] 等。
但启发式算法得到的结果只是近似解,并不适用于挖掘精确结果的情况。而近年来,精确性算法凭借其结果完全性、准确性的特点依旧是学者们的主要研究方向之一。2003年Tomita和Seki等人提出了MCQ算法 [12],MCQ算法是基于近似顶点染色的分支限界算法,其顶点染色不仅用于团上界值的估计,分支顶点的排列顺序也依赖于顶点染色的结果。MCQ采用顺序顶点染色方法,在搜索树的每个节点上对候选顶点以预先排列好的顺序,逐一为每个顶点分配其能够获得的最小颜色编号。如果染色数上界不能达到完全剪枝的目的,则所有的候选节点按照其获得的颜色编号由小到大排列(相同颜色编号的顶点排列在一起)。Tomita的实验表明,MCQ在性能上显著地超越了同期最好的其它算法。而后基于MCQ算法改进提出的MCR算法 [13] 也进一步提升了算法的性能,利用Carraghan和Pardalos提出的退化顺序作为初始顶点排列顺序。2007年Konc和Janezic延续了MCQ算法的基本框架,在顶点的排列顺序上进行了改进 [14]。沿着MCQ、MCR的算法思路,Tomita等五位研究者在2010年提出了更加高效的MCS算法 [15]。MCS算法引入了RE-NUMBER程序,对部分已染色的顶点进行重新调整,以进一步减少分支顶点数量。2013年Li和Fang等提出了IncMaxCLQ中,引入了被称为渐进上界的线性时间复杂度上界计算方法 [16]。2015年Segunda等将MaxSAT推理的思想融入到BBMC算法中,提出了改进的BBMCX算法 [17]。与Li等人的在MaxCLQ中使用的MaxSAT推理不同,BBMCX算法将MaxSAT推理限定在最多三个颜色分类中。Segunda等把运用MaxSAT推理获得的上界称为亚染色数界。实验表明集合了亚染色数界的BBMCX算法,在搜索树大小和执行时间上比其前身BBMC算法有了进一步的改进。
3. 最大团问题及基于邻接点求解最大团算法
3.1. 最大团问题描述
给定无向图G = (V, E),其中V为节点集;E为边集。若
,且对任意两个节点
有
,则称U是G完全子图。
团是指图的节点集的一个子集,使得其导出子图为完全子图,如果一个团不是其他任何团的子集,则称该团为极大团。一个图中含有节点数最多的极大团称为该图的最大团。
本文是基于邻接点求解最大团问题的,对于邻接点有以下定义:若节点u和v之间有边相连,则节点u和v互为邻接点。表1为本文最大团问题所需符号表示。

Table 1. Symbolic representation required for maximum clique problem
表1. 最大团问题所需符号表示
3.2. 基于邻接点求解最大团问题算法基本思想
由最大团的性质可知,假设无向图中包含一节点v,则节点v的邻接点可能与节点v共同组成最大团,根据此性质可以提出这么一个想法:v的所有邻接点集合
(1 ≤ i ≤ n,n为图G中的节点数)内存在节点它们之间任意两点之间都存在边相连,那么节点v与这些节点组成的图必定在包含节点v的极大团中。
由于最大团内任意节点之间均有边相连,则可在其中任意一个的邻接点集中找到其他组成最大团的节点。
基于以上,提出了一种基于邻接点的基本算法,如算法1所示。
算法1 基于邻接点求解最大团
输入:无向图G = (V, E)。
输出:Maximum-Clique(G):图G中最大团的。
变量:Maximal-Clique[k]:图G中含k个节点的极大团集合,求解过程中存储当前已经得到的极大团序列。
步骤:
1. 对利用邻接矩阵对图G中的节点及边信息进行存储。
2. 将节点vi与其邻接点集合N(vi)中的各节点分别组成C1,此时Maximal-Clique[k] = C1 (k = 2)。
3. 若N(vi)与其中各节点邻接点集的交集IN(vi) ≠ ∅,则将IN(vi)内各节点与对应C1分别组成C2,此时Maximal-Clique[k] = C2 (k = 3),并删除原先较小的Maximal-Clique[2]。
4. 重复步骤3,直到交集IN(vi) = ∅。
5. 此时Maximum-Clique(G) = Maximal-Clique[k]。
3.3. 算法示例
图1为所需求解最大团的无向图,对图1进行步骤1、2的操作。

Figure 1. Solving undirected graph required
图1. 所需求解无向图
根据算法,得到各节点的邻接表,此时得到的极大团如下所示:
C1 = {(1, 2), (1, 3), (2, 3), (2, 12), (3, 4), (3, 9), (3, 11), (3, 12), (4, 5), (4, 6), (4, 7), (5, 6), (5, 7), (5, 8), (6, 7), (7, 8), (8, 9), (8, 10), (9, 10), (9, 12)}。
第二次递归,判断组成当前Maximal-Clique[k]各vi的N(vi)中是否存在交集,若存在则加入当前极大团得到较大的Maximal-Clique[k],第二次递归结果图2所示:
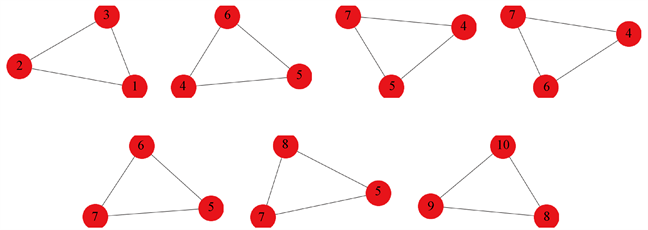
Figure 2. Maximum clique with 3 nodes
图2. 包含3个节点的极大团
第三次递归,在构成Maximal-Clique[3]的各节点的N(vi)中寻找交集,得到图3极大团:
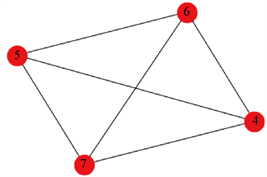
Figure 3. Maximum clique with 4 nodes
图3. 包含4个节点的极大团
此时得到的极大团包含节点数最多,即为所求的最大团。
4. 算法的正确性和完整性
算法正确性的意义是算法的结果图一定是极大团,且结果图中包含的节点数一定是最多的。算法完整性的意义是当包含节点数最多的极大团不止一个时,算法所求的结果中一定包含所有的节点最多的极大团。
引理1 对于任意的一个图,算法所求的结果图是团。
证明1) 对于任意的一个图G,经过一次递归后得到结果图Maximal-Clique[2],其中的结果图的节点集一定都包含于图G节点集,此时结果图Maximal-Clique都为团。
2) 假设当子图G的结果图Maximal-Clique为团,根据算法后续递归Maximal-Clique[k]中的节点都是图G中的节点,并且Maximal-Clique[k]一定为完全子图。
综合证明1)和2),根据数学归纳法可以得出——对于任意的一个图,基于邻接点求解的结果图必定是团。
引理2对于任意的一个图,所得到的团是极大团且一定包含所有的极大团。
证明在此算法图G中的点表示为v (图中各节点)和N(v) (各节点的邻接点集)。对于v,在算法开始时就需要遍历各节点以获得邻接点集,所以不会存在丢失任意节点的邻接点集。对于N(v),各节点都会通过邻接表存储其邻接点,因此对于任意节点其邻接点都不会丢失。
上面已经证明,在图G中包含任何节点的团中没有遗漏节点,也就是说,得到的团是一个极大团。此外,在相应的子图中可以找到包含图中任何节点的团,即它包含了所有的极大团。因此,对于任何一个图,结果图都是完备的,也就是说,结果图不仅是一个极大团,而且它包含了所有的极大团。
引理3最大团就是在极大团中含有节点数最多的一个或若干个。
证明极大团是指团内任意节点间均有边相连,且不是任何一个团的子集,而最大团则是含有节点数最多的完全子图,所以可知含有节点数最多的极大团就是最大团。
定理4基于邻接点求解最大团问题的方法是正确的。
证明由上述证明首先可知本文提出的算法对于任何求解的无向图,最后得到的结果一定是团。然后根据算法的遍历过程可知,所求结果一定是极大团,且包含所有的极大团。最后可以证明含有节点数最多的极大团就是最大团。由此可以证明算法是正确的。
定理5基于邻接点求解最大团问题是完整的。
证明根据算法的步骤3及步骤4,算法通过遍历当前组成极大团节点的邻接点来找到共同的邻接点,从而将共同邻接点加入到极大团中组成新的极大团,则可知包含图中任意一个节点的团均可以在对应的子图中找到,由此可知算法不会遗漏任何极大团,算法求解最大团是完整的。
5. 求包含任意节点的最大团
与大多求解最大团的算法相比,本算法的特点是基于节点逐渐加入邻接节点构成极大团,从而得到最大团,且不会漏掉任何一个极大团,所以算法正确性较高。
此算法第一步是得到每个节点的邻接链表,由此我们可以提出求解包含任意指定节点的最大团的应用。应用具体方式方法与本算法的区别只是在开始时就指定任意一个节点,此时定义Maximal-Clique[v]表示含有节点v的极大团,具体步骤如下:
1) 得到指定节点v的邻接链表N(v);
2) 求v邻接链表的各节点的邻接表N(vi);
3) v与其N(v)的各节点组成Maximal-Clique[v-2];
4) 判断
是否成立,若成立则将交集中的节点加入得到Maximal-Clique[v-3];
5) 重复4)直到
;
6) 此时包含节点数最多的极大团即是所要求的包含指定节点v的最大团。
以图1为例,指定求解包含节点5的最大团的过程如下:
1) 节点5的邻接链表N(5) = {4, 6, 7, 8};
2) 得到N(4) = {3, 5, 6, 7},N(6) = {5, 6, 7},N(7) = {4, 5, 6, 8},N(8) = {5, 7, 9, 10};
3) 得到包含节点5的Maximal-Clique[5-2] = {(5, 4), (5, 6), (5, 7), (5, 8)};
4) N(5)∩N(4) = {6, 7},N(5)∩N(6) = {4, 7},N(5)∩N(7) = {4, 6, 8},N(5)∩N(8) = {7}。将交集中的节点加入对应的Maximal-Clique[5-2]得到新的Maximal-Clique[5-3],如图4所示。

Figure 4. 3-Maximal-clique with node 5
图4. 包含节点5的3-极大团
5) 递归最终求得所需的包含节点5的最大团,结果为图5。
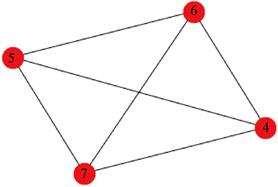
Figure 5. Maximum clique containing node 5
图5. 包含节点5的最大团
6. 总结和未来工作
本文根据最大团内两两节点间均有边相连的性质,提出了一种求解最大团问题的算法,并将该算法应用到求解包含任意节点的最大团问题当中。下一步的工作将在本文的基础上,将关联分析中的问题转化为解决图论中的问题,并将求解最大团问题应用于关联规则挖掘步骤当中。
基金项目
云南省教育厅科学研究基金项目,项目编号:2019J0008;2020J0002。云南省科技厅面上项目,项目编号:202001BB050063。