1. 引言
Hausdorff距离的相似性度量是现代相似性度量的核心之一,广泛用于工程领域:模式识别,图像匹配,人工智能的手势识别和面部识别以及定位跟踪。
现代相似性科学中常用的方法是选择空间对象的边缘轨迹并将其转换为相应的空间点集,并通过依次计算两组空间点之间的距离来确定它们之间的相似度 [1]。在基于点特征的图像匹配中,点特征是通常使用最多的特征。Hausdoff距离(Hausdorff Distance, HD)就是一种用于衡量不同点集相似程度的度量特征 [2] [3]。一般为消除或减小复杂场景下噪声对图像匹配结果造成的影响,许多研究者在标准的Hausdorff距离和部分Hausdorff距离的基础上,提出了一些改进 [4],但是改进后的Hausdorff距离计算相对复杂,难以满足实时性的要求,因而在提高匹配算法的速度方面成为研究的焦点。文献 [5] 通过降低特征点数目来减小计算Hausdorff距离的复杂程度,但其需要遍历整个特征空间。
本文针对快速图像匹配的需要,采用改进单向Hausdorff距离方法实现图像的快速匹配。
2. 图像匹配的关键问题
图像匹配是指使用特定的匹配算法对两个或更多图像执行空间相似性配准并搜索其空间变换的过程 [6] [7]。匹配过程中通常使用两个词:基准图和实时图。
基准图和实时图是同一对象的不同描述。其公式如下:
(式2-1)
式2-1中
为噪声,可通过对应的滤波方法进行去除。
,
为
上的点在图像中x和y方向上的位置偏差,这称为定位噪声 [8] [9],通常是由图像的几何变形造成的。
模板参考图像的二维像素矩阵可描述为:
(式2-2)
式2-2中
为基准图的高度和宽度。
实时图像二位矩阵为:
(式2-3)
式中
为实时图的高度和宽度。
假设参考图像坐标系的原点设置在基准图的第一个像素处,当它们匹配时,基准图中实时图像第一个像素的位置,可以确定建立坐标系。
3. Hausdorff距离
Hausdorff距离定义
Hausdorff距离是描述两组点集之间相似度的量度 [10] [11] [12]。它是两组点之间距离的一种定义形式:假设有两组点集
,
,那么,这两组点集之间的可以Hausdorff距离定义为:
(式3-1)
其中,
(式3-2)
(式3-3)
是点集A和点集B之间的距离范式。
在式3-1中通常被称为双向Hausdorff距离 [11] [12],它是Hausdorff距离的最标准形式。式3-2中
是从集合A到集合B的集合的Hausdorff距离,式3-3中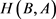 是从集合B到集合A的Hausdorff距离,即
首先对点集A中的每个点
与邻近该点
的B集中的点
之间的距离
进行排序,然后将所得距离中的最大值作为
。由式3-1知,双向Hausdorff距离
是单向距离
和
其中的数值较大者,它是两个点集间的最大不匹配程度度量标准。
是从集合B到集合A的Hausdorff距离,即
首先对点集A中的每个点
与邻近该点
的B集中的点
之间的距离
进行排序,然后将所得距离中的最大值作为
。由式3-1知,双向Hausdorff距离
是单向距离
和
其中的数值较大者,它是两个点集间的最大不匹配程度度量标准。
4. Hausdorff距离的特点及改进方法
4.1. 改进Hausdorff距离
本文采用单向Hausdorff距离算法对图像进行匹配,可以有效解决复杂图像中存在噪声。匹配时,对目标区域和模板图像进行相似度计算,从而确定相似度最高的区域。在单向Hausdorff距离,其中,
(式4-1)
式4-1中,
为点集A中元素的个数。
为解决复杂环境下噪声对图像匹配过程中造成的影响,在基于单向Hausdorff距离上,构造了代价函数的Hausdorff距离,其定义为:
(式4-2)
其中,
为代价函数,其定义为:
(式4-3)
通过阈值
来去除距离相对较大匹配点,同时求其平均值,因而降低了在复杂环境下噪声影响,因而在图像匹配时有较好的匹配效果。
4.2. Hausdorff距离模板匹配
在图像匹配过程中,模板图像在待匹配图像上进行滑窗移动,得到最优的匹配区域。通常,在模板图像和待匹配图像已知的情况下 [13],模板图像移动的次数则可以计算出来的。对于图像I和模板M中,经过二值化处理可得矩阵
和
,在平移距离为
的情况下,则Hausdorff距离为:
式(4-4)
在对M和I进行距离变换,则单向Hausdorff距离为:
式(4-5)
式(4-6)
在图像匹配时,单向Hausdorff距离的第L和第K的最大值为:
式(4-7)
式(4-8)
式4-7、式4-8中,p、q为图像I和模板M的像素数,
和
为控制匹配参数,其中
。单项距离大大减少了图像和模板匹配所需的时间。
5. 试验结果与分析
试验运行环境为win10家庭版,matlab版本为2014b,图像为80幅教学楼以及采集的20幅校门建筑图像,总计100幅。实验参数中阈值
,对待检测的图像进行规格化,进行了实验对比,其结果如表1、表2。

Table 1. Performance comparison of different inspection methods for school gate buildings
表1. 对校门建筑不同检测方法性能比较

Table 2. Performance comparison of different inspection methods for teaching buildings
表2. 对教学楼建筑不同检测方法性能比较
从表1和表2的三种检测方法统计结果可以看出:标准的Hausdorff距离进行检测时,采用双向计算,匹配准确,但运算量过大,对采集图像无法快速处理,容易导致程序瘫痪;在单项Hausdorff距离检测图像会使检测时间大幅度降低但其检测准确率也相应下降,其误检率也相应升高;而本文提出的基于改进的单项Hausdorff距离的图像匹配算法,在提升准确率的同时也相应地缩短了时间,对在复杂的场景下(如图1、图2所示)也具有一定的鲁棒性。
改进后代价函数Hausdorff距离匹配准确率明显提高,因而,匹配算法匹配的正确率与其处理的图像相关,比如原图像的边缘复杂程度,还有它们之间存在的变换有较大关系。匹配图像的多余边缘的干扰越小、边缘线越清晰,匹配效果也会越好。对于模板到源图像的变换过程,变换越简单,其匹配效果也会越好。

Figure 1. School gate building improvement Hausdorff distance template matching image
图1. 校门建筑改进Hausdorff距离模板匹配图像

Figure 2. Teaching building construction improvement Hausdorff distance template matching image
图2. 教学楼建筑改进Hausdorff距离模板匹配图像
6. 结语
本文给出了一种基于Hausdorff距离的图像匹配算法,该方法根据Hausdorff单向距离搜索图像的距离图,进而检测出目标图像,可以在复杂的场景中检测出目标,体现出该方法的有效性。以Hausdorff距离作为相似性度量具有很好的容错性和抗干扰性,通过改进单向Hausdorff距离,来提高准确率和实时性,从而降低图像因距离变换空间进行搜索的时间。目前,该方法精确度有限,改进思路是:将其它特征加入到该检测依据中,进一步提高该方法的抗干扰适应能力和准确率。