1. 引言
约束优化问题是在给定约束条件下对目标函数进行优化的问题 [1],在实际应用中经常出现。具有不等式、等式、上界和下界约束的一般约束优化问题定义为:
(1)
其中
为n维变量,f(x)为目标函数,g(x)为不等式约束,h(x)为等式约束,j为不等式或等式约束的个数,li和ui分别是xi的下界和上界。上下界定义了约束优化问题的搜索空间,不等式和等式定义了可行域。可行域或边界上的点称为可行点,否则即为不可行点。
由于约束优化问题的复杂性,传统的进化算法难以求解。同时,进化算法大多是基于无约束优化问题的搜索技术,在应用进化算法求解约束优化问题时,其最优解可能不精确。因此,有必要结合合适的约束处理技术来处理约束优化问题。
本文提出了一种基于约束一致策略的人工蜂群算法(ABCCC)。人工蜂群算法(Artificial bee colony, ABC)是由Karaboga提出的一种最新的启发式算法,其灵感来自于蜜蜂的觅食行为,用于求解数值优化问题 [2]。相对于差分进化算法(DE)和粒子群算法(PSO),ABC算法有两个明显的优势:1) ABC在局部优化和全局优化方面都很好。2) ABC灵活、稳健、使用简单,它可以有效地应用于多模态、多变量问题的优化。为了驱动个体向可行域移动,在ABC算法中引入了约束一致策略。CC策略具有以下优点 [3]:1) CC策略易于实现。2) CC计算量小,计算稳定性好。为了有效地结合ABC算法和CC策略,文中重新设计了对不可行个体的处理。即部分不可行个体采用CC策略进行进化,其余不可行个体和可行个体采用ABC算法进行再生。为了验证ABCCC的特性,采用CEC2017基准函数对其性能进行测试。实验表明,在大多数情况下,ABCCC收敛速度较快,收敛精度较好,并且能较好地考虑种群多样性问题。ABCCC与DECC和PSOCC相比也更具竞争力。然后利用ABCCC算法与其他算法(CALSHADE [4]、UDE [5]、CABC [6] 和GABC [7] )进行了比较。实验结果表明,ABCCC算法的性能优于其他算法。
本文组织结构如下,引言后,第2节详细阐述了约束一致策略,第3节介绍了人工蜂群算法,新算法的详细信息见第4节,第5节给出了实验结果和分析。最后,第6节对全文做了总结。
2. 约束一致策略
约束一致策略(Constraint Consensus Strategy, CC)是一种同步分量平均梯度投影算法 [8] [9] [10],主要的思想是通过采取某些行动,在当前违反的约束之间产生一个在行动的方向和距离上“一致意见”的结果,根据这个结果改进当前的不可行点以实现可行性。
约束一致策略算法的第一步就是找到在当前点x处违反的每个约束的可行性向量,对于每个约束违反,可行性向量近似从当前的不可行解到最近的可行解的移动。它对于线性约束是精确的,但对于非线性约束只是一个估计。衡量不可行点到可行区域的距离是点与可行区域之间的最小欧几里得距离,称为可行性距离 [11]。可行性向量的计算公式如下:
(2)
其中,Ñc(x)是约束的梯度,||Ñc(x)||是它的长度;v是约束违反量,当满足约束条件时v = 0;d是一个方向参数,如果有必要增加c(x)满足约束条件则d + 1,如果有必要减少c(x)来满足约束条件则d − 1。可行性向量的长度表示为||fv||,也即可行性距离。

Table 1. Pseudocode of constraint consensus strategy
表1. 约束一致策略
第二步是对所有违反约束的可行性向量进行组合,得到实际用于更新的一致向量。这个过程是以组件方式完成的:只有在c(x)中包含特定变量的违反约束才能对该维度中的移动进行“投票”。通过对各可行性向量的相关分量进行平均得到各维度的运动,产生的一致向量指定了移动的方向和距离,应用一致向量来更新当前点。这两步不断重复直至满足终止条件。约束一致策略的算法步骤如表1所示。NINF是当前违反约束的数量,sj表示变量xj的fvij对所有违反约束条件的可行性向量的和,nj代表以变量xj为组件的违反约束的数量,fvij表示第i个约束的可行性向量中变量xj的分量,t为一致向量。如果这个向量太短,那么迭代将停止,结果是失败的。当每个约束的约束违反量为零或可行性距离小于a,即NINF为零时,算法停止 [8]。
约束一致策略的方法是简单的,缺点在于,单个可行性向量组合的方法可能会被特殊情况所阻碍,特别是一组向某个方向拉动的可行性向量与另一组向相反方向拉动的可行性向量相平衡时。但是,当约束一致策略与进化算法一起使用时,这样的个体不会产生任何问题。
3. 人工蜂群算法
人工蜂群算法(Artificial Bee Colony, ABC),是由Karaboga发明的一种基于群体的随机优化方法,它模拟了蜜蜂的智能觅食行为,蜜蜂根据各自的分工进行不同的活动,并实现蜂群信息的共享和交流,从而找到问题的最优解。

Table 2. Pseudocode of ABC algorithm
表2. ABC的伪代码
在一个自然的蜂群中,通常有三种觅食的蜜蜂,分别是雇佣蜂、旁观蜂和侦查蜂。蜂群的一半是雇佣蜂,另一半是旁观蜂。雇佣蜂负责在自己的蜜源周围搜寻,同时向旁观蜂传递高质量的蜜源信息。旁观蜂根据收到的信息,倾向于选择更好的蜜源进行开采。若某蜜源在规定迭代次数内未更新,则雇佣蜂抛弃该位置转化为侦查蜂,去随机寻找新的蜜源 [1] [12]。表2列出了人工蜂群算法的伪代码。
人工蜂群算法中,蜜源的位置表示优化问题的解,每个蜜源的花蜜量表示相应解的适应度值。首先,对蜜源的位置进行初始化,雇佣蜂(或旁观蜂)的数量等于蜜源的数量:
(3)
其中,i = 1, 2, …, SN,j = 1, 2, … D,SN是蜜源的数量。D为决策变量的维度,表示待优化参数的个数。xmax j和xmin j分别是蜜蜂在第j维坐标位置的上界和下界。另外,在此阶段,存储每个蜜蜂试验次数的计数器被设置为0。
初始化阶段结束后,ABC进入雇佣蜂、旁观蜂和侦查蜂阶段的循环,直到满足终止条件。在雇佣蜂阶段,每只雇佣蜂对应一个确定的蜜源并在迭代中对邻近的蜜源进行搜索,根据式(4)产生相邻的蜜源:
(4)
k是不同于i的随机蜜源,j是随机选择的维度。f是在[−1, 1]范围内的一个均匀分布的随机数,决定了扰动程度。通过改变x上的一个维度来确定新的蜜源v,如果这个操作产生的这个维度的值超过了预定边界,就把其设置为边界值。
然后评估新蜜源的适应度值,当新蜜源v的适应度优于x时,采用贪婪选择法用新蜜源代替原来的蜜源,否则保留x。如果蜜源发生了变化,试验计数器将重置为零;否则,其值将增加1。所有的雇佣蜂完成该步骤的运算后,飞回信息交流区共享蜜源 [13]。
在旁观蜂阶段,旁观蜂接收到雇佣蜂共享的蜜源信息,然后他们会根据蜜源的花蜜量的概率,各自选择一种蜜源进行开发。概率的计算公式如(5)所示:
(5)
人工蜂群算法中,解的适应度评估根据公式(6)计算,fi表示解的函数值:
(6)
旁观蜂采用轮盘赌的方法选择蜜源后,每只旁观蜂会像雇佣蜂一样,按照公式(4)在其附近继续寻找新的蜜源。
在侦查蜂阶段,引入一个叫做“limit”的控制参数来决定是否抛弃某一蜜源。如果该蜜源没有在“limit”预定的周期内得到改善,那么该蜜源就会被抛弃,并且对应该蜜源的雇佣蜂转化为侦查蜂。接着使用(3)在搜索空间中随机产生一个新的蜜源,就像初始化阶段一样。
(7)
4. 基于约束一致策略的人工蜂群算法
该章节中,将详细介绍基于约束一致策略的人工蜂群算法的内容。图1是该算法的流程图。根据流程图可以看出,种群在处理的过程中,根据个体是否可行分成了两部分,一部分是少量的不可行个体,另一部分则是可行个体和剩余不可行个体的集合。然后分别采用约束一致策略和人工蜂群算法处理两部分种群个体。
在该算法中,首先随机初始化一个种群P,然后评估种群当前的适应度值和约束违反程度,根据约束违反程度可以找到当前种群状态下的可行个体集合和不可行个体集合。假设初始化后的种群中存在的不可行个体为SP,在SP中选取部分不可行个体,记为SSP(即只选取部分不可行个体,而不是全部的不可行个体SP),基于章节2介绍的约束一致策略,对SSP个不可行个体进行处理,产生原部分不可行个体的新位置。随后,剩余的不可行个体与可行个体合并,将经典的人工蜂群算法应用于该个体的集合。算法之所以只选取部分不可行个体进行操作的目的是可以节省计算时间,不可行个体越多,约束一致策略运行的时间越长,另外一个目的则是能够保持种群的多样性。
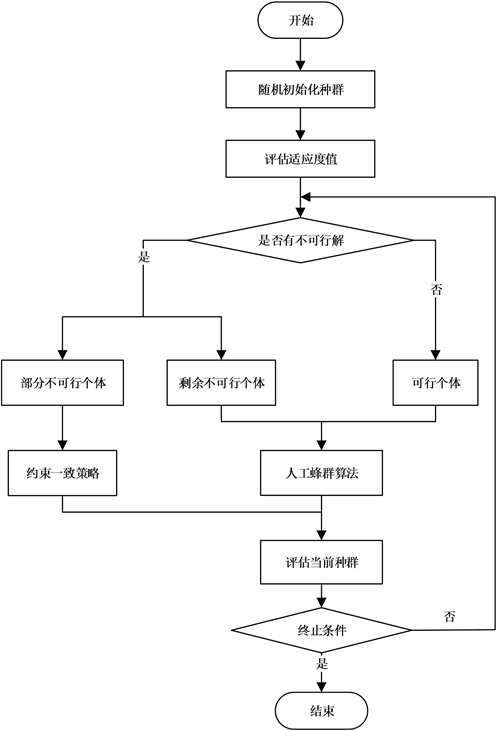
Figure 1. Flow chart of the ABCCC algorithm
图1. 基于约束一致策略的人工蜂群算法流程
初始种群P采用如下公式生成:
(8)
其中,Ud和Ld是决策变量的上下界,d为变量的维度。rand(0, 1)表示(0, 1)范围内的随机数。xi,d即代表初始的种群个体。
接下来,计算初始化种群P内全部个体的适应度值和约束违反量,如果所有约束的违反量均小于等于0,表明当前个体没有违反约束,是可行的个体,这样的个体暂时不采取任何措施,等待后续与剩余不可行个体合并直接采用ABC进化。如果至少有一个约束产生违反,即约束违反量大于0,那么这个个体就是不可行个体,所有不可行个体的集合为SP。
当不可行个体的集合SP不为空时,在SP内随机的选取SPP个不可行个体,利用前面章节介绍的约束一致策略,改变当前SPP个不可行个体的位置。个体的改变依照公式(9)进行。即对每个不可行个体,计算出针对它的一致向量t,将当前的位置与向量的坐标相加得到个体的新位置,新个体记为x’i,d。剩余的不可行个体和原先找到的可行个体形成的合集利用人工蜂群算法进行演化。若SP的集合为空时,说明当前迭代下没有不可行个体,此时,所有的可行个体直接利用人工蜂群算法产生后代,寻找最优解。
(9)
需要注意的是,在人工蜂群算法原来的贪婪选择操作下,做了一点改动,将可行性规则引入对个体进行选拔,即个体的选择需要同时考虑目标函数值和约束违反程度。当个体均可行时,目标函数值越小(极小化问题),个体的解最优;当可行个体与不可行个体同时存在,可行个体的解总是优于不可行个体的解;当同为不可行个体时,选取约束违反量总和最小的解予以保留。
该算法中,等式约束的处理将转换为公式(10)的不等式,e是一个容差值,实验中取值10−4。
(10)
算法的伪代码如表3所示:
5. 实验结果与分析
该章节主要列举和分析了ABCCC算法的实验结果,首先在指定的测试函数集进行测试,找到了测试集的优秀结果,验证了该算法能够用来解决约束优化问题。接下来,还将ABCCC与DECC和PSOCC算法进行了对比(把ABC替换为差分进化算法(DE)和粒子群算法(PSO)),实验结果表明,ABCCC优于其余两个算法。同时该章节还分析了算法内部参数对实验结果的影响。最后将ABCCC算法与其他较优秀的算法进行了比较,实验表明了ABCCC在解决约束优化问题上具有一定的竞争力。
5.1. 测试函数集与参数设置
通过求解CEC2017约束优化测试函数集中的部分函数,对算法进行了测试 [14]。函数集中的问题具有不同的数学特征,比如有的目标函数或约束是线性或非线性的,有的约束是等式或不等式,有的目标函数是单峰或多峰。并且有的函数是可行空间非常小,这更增加了解决问题的难度。
算法的参数设置包括如下内容:种群P的大小为100,选择SPP个不可行个体的依据是SPP = 0.5SP (在5.3章节讨论为什么将比例设置为0.5),总迭代次数设为100,每个问题独立运行的次数为10次。对比算法DECC和PSOCC的参数设置为:DE的变异因子F设为0.5,交叉因子CR设为0.4;PSO的学习因子C1和C2相等,取值均为1.4,惯性权值w设为0.8。约束一致策略的参数设置如下:可行距离的容差值a设为10−6,移动容差值b为10−4。
5.2. 实验结果
在本节,首先列出了ABCCC在CEC2017函数集下的实验结果,同时还对比了DECC和PSOCC在相同状况下的实验结果,表4列出了实验过程中得到的最优解、平均值和标准差。最优解表明算法在解决该问题时找到的目标函数的最小值,平均值反映了10次运行的平均结果,标准差则能表明算法的鲁棒性,标准差越小,表明算法每次运行得到的结果都是近似的,说明算法是稳定的。实验结果表明ABCCC的算法性能总体上要优于DECC和PSOCC,收敛迅速且能找到最优解。
从表4可以看出,ABCCC算法得到的最优解和平均解在大多数函数(C01、C02、C03、C04、C05、C06、C07和C09)的表现都优于DECC和PSOCC。而对于函数C08和C10,DECC得到的结果则是最小的,优于PSOCC和ABCCC。其中有一个函数C09,该函数在ABCCC和PSOCC下取得的最优解相同。

Table 4. Comparison results of ABCCC, DECC and PSOCC
表4. ABCCC与DECC和PSOCC的对比结果
从图2所示的收敛曲线图可以看出,ABCCC比其他算法收敛速度更快,收敛结果较优,得到了更理想的全局最优解。然而,函数C08和C10则是DECC得到的解更优。
图3给出了算法的盒图。对于每个盒图,中心标记表示中间值,方框的底部和顶部边缘分别表示第25百分位数和第75百分位数。胡须延伸到不被认为是异常值的最极端数据点,并使用“+”符号分别绘制异常值。从图3可以看出,ABCCC在大部分测试函数(C01、C02、C03、C04、C05、C06、C07、C09)均是性能较优越的。
5.3. SPP值对ABCCC的影响
在5.1章节中,SPP参数的选取为0.5,即选取了不可行个体的一半,在该章节中,我们将测试SPP值对算法性能的影响。
处理不可行个体时,5.1节中介绍的是在所有的不可行个体中只选取部分个体,因此本节按照不同比例范围选值进行测试,其中SPP设置为0.1SP、0.3SP、0.5SP、0.7SP和0.9SP (SP即为前面章节介绍的全部不可行个体)。SPP值越高,预计搜索周期越长,具体的实验结果如表5所示。从搜索周期的角度看,SPP的值越小,搜索的时间越短,所以当SPP = 0.1SP时算法会更好,因为它的运行时间相对最短。但是从解的质量角度看,当SPP = 0.5SP时,大多数函数的实验结果比其他情况较好,尤其是平均适应度值的结果。因此ABCCC算法中SPP值的选取为0.5时更合适,能够解决大部分的测试函数问题。


Table 5. The influence of SSP on results
表5. SPP值的选取对算法结果的影响
图4为测试函数C02的收敛曲线图,从图中可以明显地看出,SPP = 0.5SP时收敛速度更快,得到的最优解更好。

Figure 4. Convergence curve of ABCCC under different SPP values (C02)
图4. 不同SPP值下ABCCC的收敛曲线图(函数C02)
5.4. ABCCC与其他算法的比较结果
在该章节,ABCCC算法与其他的算法进行了比较,具体的实验结果展示在下面的表6中。ABCCC先与CALSHADE和UDE进行了实验对比,结果表明ABCCC能取得大多数测试函数的最优解。但对于函数C01和C02,CALSHADE算法取得了函数的最优解;对于函数C08和C10,算法UDE的表现更好。但从整体来说,实验结果表明ABCCC算法的性能优于其他算法。

Table 6. Comparison results of ABCCC、CLSHADE and UDE
表6. ABCCC与CLSHADE和UDE算法的比较结果
人工蜂群算法在后来的研究中被许多研究者提出了一些变体,比如CABC和GABC,因此该章节也将ABC算法替换为CABC和GABC,将这些算法进行了比较,结果如表7所示。除了测试函数C01,C08和C10外,ABCCC在其他测试函数中均能够找到最优解。而函数C01和C08的最优解由GABCCC找到,对于C10,则是CABCCC获得了最小值。究其原因,GABCCC利用全局最优值在搜索周期中对个体进行变异,对结果的影响较大。虽然CABCCC基于随机选择的某个维度对每个个体进行变异操作,但也降低了收敛速度,导致搜索周期变长。

Table 7. Comparison results of ABCCC, CABCCC and GABCCC
表7. ABCCC与CABCCC和GABCCC算法的比较结果
6. 结论
在过去的几十年里,许多进化算法被引入来解决约束优化问题。然而,在进化优化中缺乏有效的约束处理机制。在本研究中,基于约束一致策略的有效性,提出了一种新的人工蜂群算法。为了使计算时间最小化并保持种群内良好的多样性,对每代不可行个体采用基于约束一致方法的更新策略,剩余个体(包括可行个体和不可行个体)采用人工蜂群算法进行演化。
该算法在一组约束问题上进行了测试。实验还比较了ABCCC与DECC和PSOCC的性能。结果表明,在大多数情况下,ABCCC算法比其他两种算法都能获得更好的结果和更快的收敛速度。该算法还与CLSHADE、UDE等算法进行了比较,实验结果表明,ABCCC算法性能良好,能得到最优解。此外,与采用CC策略的ABC的变体相比,我们的ABCCC算法的结果优于其他算法。
在未来的工作中,我们还将分析不同参数值对该算法性能的影响,并尝试进一步改进所提出的算法。