1. 引言
传统的PID控制因其算法可靠简单,鲁棒优良,可靠度高,在工业过程中得到了广泛的应用,特别适用于建立一个精确的数学模型确定控制系统的确定性控制。李文宇等对PID控制进行了研究,并取得了一定的应用 [1] - [7],但在非线性、时变、耦合和参数及结构不确定系统中,传统的PID控制器参数整定比较困难,结果会使得系统性能变差,导致工况适应性不好。另外针对复杂的控制过程,传统PID控制器制效果更差,特别是参数调节无法达到理想效果。基于这一点,为了拓展PID控制器适应范围,特别是复杂工况和控制高要求情况,参数自动整定对PID控制器尤为关键。随着时代的进步,数字智能控制器已经出现,开始应用实际生产中,参数自动整定可以智能实现,文献 [8] - [13] 将PID控制和模糊控制相结合进行研究,并在某些领域取得了不错的效果。本文结合了模糊控制与PID控制,运用模糊推理方法,在线实现对PID参数自整定,调整最佳PID参数,设计了参数模糊的自整定PID控制器,并举例使用MATLAB对系统进行仿真。
在PID控制器参数模糊自整定系统中,把偏差
和偏差变化率
作为输入,通过模糊推理的方法,可以实现PID参数
和
不同时刻自整定需求。便构PID控制器参数自整定,参数模糊自整定如图1所示。
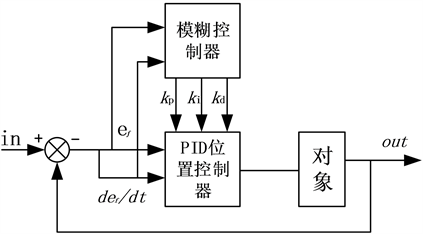
Figure 1. Fuzzy self-tuning PID controller structure
图1. 模糊自整定PID控制器结构
模拟PID控制器是线性控制器,是连续的,表达式如式(1)及式(2)所示。
(1)
(2)
式中,
——比例系数;
——微积常数;
——微分常数;
为输入信号;
为输出信号;
为控制器输出。
数字PID控制器有位置式及增量式,表达式如式(3)及式(4)所示。
(3)
(4)
式中,
,
,T为采样周期,k为采样序号;
为第k次采用时刻的计算机输出值。
PID控制器的参数
,
,
调整,是利用模糊规则找到其与输入误差
和误差变化率
之间关系,在系统运行时通过一个持续的模糊检测
和
,根据模糊控制处理原则对3个控制参数分别进行在线的模糊修改,以便达到系统动态、静态性能要求。
2. 糊控制器的设计
2.1. 语言变量隶属度函数的确定
模糊PID控制是通过计算机采样被控对象的精确值,并与给定值比较,得到误差
,并误差变化率
一起作为模糊控制器的输入量。再经过根据模糊推理得到ID参数
,
,
,这样可以使不同时刻的
和
对PID参数自整定要求得到满足。其中
,
,
为预整定值。
,
,
。
对于两输入(
和
)和控制器三输出(
,
,
)都采用如下模糊集:
{负大,负中,负小,零,正小,正中,正大},用英文字头缩写为{NB, NM, NS, ZO, PS, PM, PB},其中
和
的论域为[−3, −2, −1, 0, 1, 2, 3],
,
,
的论域为[−6, −4, −2, 0, 2, 4, 6],隶属函数曲线见图2。
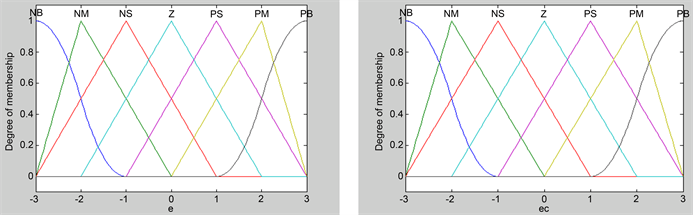
Figure 2.
and
membership function curve
图2.
和
隶属函数曲线
,
,
的模糊规则表建立好后,可对
,
,
进行自适应校正。应用模糊合成推理设计PID参数的模糊矩阵表,查出修正参数代入式(5)计算:
,
,
(5)
具体实现如工作流程图3所示,完成对PID参数在线自动校正。其隶属函数为:
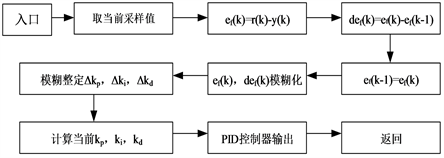
Figure 3. The flow chart of fuzzy PID control online self-correction
图3. 模糊PID控制在线自校正流程图
2.2. 建立模糊控制器的控制规则表
系统输出特性关键是对参数
、
和
的整定,参数
、
和
又与输入参数
和
有关,参数
、
和
自整定原则如下:
1) 当
数值大时,无论误差是变大还是变小,都选择
最大(或最小)值输出,这样就能够对误差迅速调整。另外为了避免积分饱和现象,此时参数
取值应较大,参数
取较小值,参数
取零。
2) 当
时,即误差绝对值在增大。当误差绝对值较大时,加大控制器控制作用,使得误差绝对值朝变小,此时参数
取值应较大,参数
也不能太大,参数
取较小的值。另外当误差绝对值较小时,控制器只需要作较小调节就可以,只要阻止误差绝对值变大即可。
3) 当
或
时,说明系统误差小,实际值与理论值接近,或者系统处在一个平稳状态。此时,控制器输出可保持不变。
4) 当
,
时,表明实际值与理论值差值恒定或一致,系统处于稳态性能状态,参数
和
采取较大值,另外选取
值适当可以避免误差在给定值附近振荡。设
(6)
式(6)中
,
和
为传统PID参数,其值通常采用Z-N法确定。根据专家经验和PID参数的整定规则,用IF-THEN方式,得到
、
和
整定规则,如表1所示。


Table 1. The fuzzy rules of Δ k p , Δ k i , Δ k d
表1.
的模糊规则
根据误差
和误差变化率
的论域值,为模糊控制量的论域值:
模糊控制子集可表示为:
。由两输入(
,
),再根据三个参数模糊规则表构造一个三输出(
)的模糊控制器。
3. Matlab仿真
3.1. 模糊控制器的编辑
打开Matlab软件,运行Fuzzy函数,并新建一个的FIS文件,分别定义参数隶属函数和量化区间,定义输入模糊控制规则。设与(and)为min,或(or)为max,推理(implication)为min,合成(aggregation)为max,去模糊化(defuzzification)为重心平均(centroid),FIS系统文件就建立了。
3.2. 仿真实例
设被控对象传递函数为
根据模糊规则和隶属函数,对PID控制进行仿真,设参数
、
和
,相应响应曲线见图4~7。
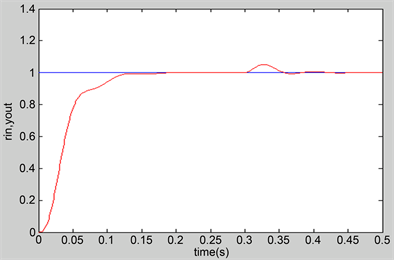
Figure 4. Fuzzy PID control step response
图4. 模糊PID控制阶跃响应
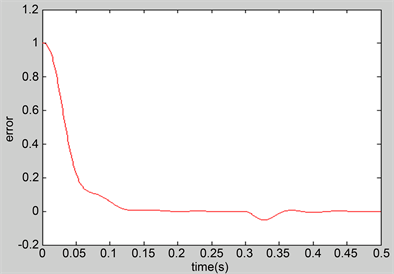
Figure 5. Fuzzy PID control error response
图5. 模糊PID控制误差响应

Figure 7. The self-tuning process of
,
and
图7.
、
和
的自整定过程
由于传递函数是一个3阶对象,传统的PID控制参数不容易得到理想结果,主要是整定
、
和
3个参数,用模糊规则对PID参数进行自整定后,明显得到了不错的控制效果。从图可以看出系统的性能有着良好的稳定性和快速性收敛性,该控制方案具有很好的应用价值。
4. 结束语
模糊PID自整定控制继承了模糊控制和PID控制的优点,摒弃了两者的缺点,用模糊推理规则,实时整定PID的参数,获得理想参数,另外又通过对一个3阶对象进行仿真,得出该方法对系统的稳定性和快速反应有明显提高。该方法简单易用且实现方便,对现实控制有一定的参考意义。
基金项目
江苏省高等学校大学生创新创业训练计划项目(201912920001Y);南京科技职业学院资助项目(NHKY-2017-06,NHKY-2017-14) 。
NOTES
*通讯作者。