可移动应急电源在电力–交通网络中的配置与调度研究

Research on Configuration and Scheduling of Mobile Emergency Power Supply in Power Transportation Network

摘要: 考虑到不确定性极端事件的到来会对电力网和交通网同时造成破坏，本文利用可移动电源作为电力交通网耦合的桥梁，通过最短路径算法研究应急电源的移动规律，使应急电源能够最快地对电力系统重要负荷进行修复，减小系统损失。为更好地提高电力系统生存抵抗力和恢复力，分别对应预置和调度两个阶段，本文第一阶段建立了一个针对多场景下电力–交通网破坏的应急电源预置模型，考虑了电力系统常规约束、应急电源位置约束等，同时采用改进后的Dijkstra算法对道路破坏的交通系统进行处理求解出任意节点间的移动距离，第二阶段建立了灾害到来时应急电源实时调度模型，考虑电力交通相关约束，最后该两阶段模型在python-gurobi上实现，案例采用IEEE33节点系统，求解得出应急电源预置和调度结果。

Abstract: Considering that the arrival of uncertain extreme events will damage the power and traffic network at the same time, this paper uses the mobile power source as the coupling bridge of the power and traffic network, and studies the movement rule of the emergency power source through the shortest path algorithm, so that the emergency power supply can repair the important load of the power system as soon as possible and reduce the system loss. In order to improve the survivability and resilience of the power system, in this paper, we first establish an emergency power source preset model for multi-scenario power-traffic network disruption, which takes into account the conventional constraints of the power system and the location constraints of the emergency power source. At the same time, the improved Dijkstra algorithm is used to deal with the traffic system with road damage and solve the problem between any nodes in the second stage. The real-time dispatching model of emergency power source is established when the disaster comes. Considering the constraints of electric power and transportation, the two-stage model is implemented on Python gurobi. The IEEE33-node system is used in the case, and the preset and dispatching results of emergency power sources are obtained.

1. 引言

近年来极端事件的频繁发生及其带来的重大破坏对电力系统正常运行造成了极大的冲击。极端事件包括自然灾害和人为操作失误，针对自然灾害，提高电力系统弹性可以及时应对和处理自然灾害突来给电力系统带来的破坏。弹性概念最早由生态学家Holling将其引入到生态学研究领域 [1]，随后逐渐应用于评估包括电力系统在内的基础设施系统承受外部扰动及扰动后恢复的能力研究 [2] [3] [4]。弹性(resilience)是指系统能够预防、抵抗、适应和从干扰中恢复的能力。电力系统弹性比可靠性更难提高，系统更难应对极端事件的到来 [5]。文献 [6] 同时给出了反应电网弹性的三个阶段性特征，这里主要针对极端事件发生前的预防性调整能力和极端事件发生后的快速恢复能力。在过往的研究中，常用的提高电力系统弹性的方法主要有加固电力系统元件，如杆塔、线路等等 [7]，但这些措施应对极端事件到来造成的重要负荷中断没有好的修复效果。也有部分研究考虑了移动电源来恢复电力系统弹性，如文献 [8] 提到利用移动电源(MPSs)来增强配电系统(DS)抵御极端天气事件，提出了一种求解MPS调度与DS运行不同时间尺度、道路与电网耦合等问题的混合整数规划模型，以优化MPSs的动态调度。文献 [9] 中加入了维修人员(RCs)修复线路和移动电源(MPSs)移动恢复相搭配，提出一种新的协同优化模型包含了DS恢复和RC/MPS调度的不同时间尺度，交通和电网的耦合。文献 [10] 提出了同时对电力网和交通网进行修复，建立一个耦合修复模型，在最大化恢复负荷的前提下得出了电力交通网最佳的修复顺序。文献 [11] 研究表明需要同时考虑电力和交通网的弹性，通过修正交通配流模型来实现交通网的弹性恢复。

上面都提到了要考虑应急电源移动时对于交通系统的影响，但不明确，都是给出了一些假设条件。下面部分考虑到了实际存在的应急电源移动与交通系统的关系，如文献 [12] 指出MEGs是电力系统快速恢复的宝贵的灵活性资源，文中方法明确考虑流量问题，主动执行预定位，可以减少临界负荷停机时间。在实时分配中，实现了MEGs与负载的合理匹配，引入了由预定位和实时分配组成的两阶段调度框架，并通过车辆路径问题来考虑交通问题。文献 [13] 在考虑交通问题时采用深度学习对城市道路旅行时间进行预测，考虑空间相关性的LSTM模型具有更好的拟合实际出行时间的能力。文献 [14] 提到车辆出行路径与目的地选择有关，构建了交通分流双层规划模型，采用用户均衡模型求解，验证其有效性。

谈到电动汽车与电力交通耦合网关系，文献 [15] 中先建立了含电动汽车的电力交通耦合数学模型，再考虑电动汽车负荷对电网潮流的影响，最后研究了道路破坏对电动汽车出行路径的影响，初步引入了交通道路破坏的影响。

上述文献中已经提到了利用移动电源来为系统中因为极端事件造成的重要中断负荷及时供电，减小重要负荷中断的时间，同时，移动电源的移动必然对交通系统正常移动规律特性产生影响，道路破坏时也将影响路径及移动距离，需要同时研究交通系统弹性，在道路遭遇破坏时使出行路径最短，目前交通系统中主要用到车辆配流和Dijkstra算法来研究车辆移动路径及移动时间。

基于以上分析，极端事件下应急电源在参与电力系统弹性恢复过程中还与电源在交通系统中的移动路径及距离有关。本文首先建立了一个第一阶段的多场景下电力–交通弹性恢复耦合模型，以极端事件下最大化恢复电力系统负荷、最小化应急电源移动距离为目标，考虑电力、交通常规约束，求解出应急电源的初始配置结果。第二阶段建立了特定场景下的应急电源实时调度模型，以灾害发生后的短时间内失负荷量最小为目标，考虑不同时刻下负荷的实际变化情况，考虑应急电源在交通网中的实际出行约束、电网中的常规约束等，最后在Python3.7上编程实现，以IEEE33节点作为算例，求解出电网恢复情况与应急电源实时移动路由。

文章结构如下：第一部分介绍了可移动应急电源分类、特点以及在交通网中的移动模型。第二部分介绍了为应对极端事件的不确定性，提高系统的生存抵抗力，考虑电力线路和交通道路同时破坏情况，建立了可移动应急电源预置模型。第三部分主要为灾害发生后提高系统的恢复力，建立特定场景下应急电源实时调度模型，针对灾害发生后不同时刻负荷变化情况，建立起电源实时接入位置与移动时间之间的联系，实现短时间内最快最大化恢复负荷。第四部分是介绍针对极端事件的不确定性采用多场景方法和道路破坏时采用更新的Dijkstra算法处理交通系统问题。第五部分是以33节点系统作为算例进行分析验证模型，先后设置预置和调度算例，对结果进行分析对比。最后一部分是结论与展望。

2. 考虑电力–交通耦合的可移动应急电源

电力系统元件(如杆塔和线路等)因为极端事件的到来而遭到破坏时，一些地方的重要负荷将会发生中断供应，当重要负荷短时间得不到电力供应时而造成电力系统损失巨大，传统的恢复方法短时间内很难起到立竿见影的作用，此时应急电源的灵活方便性便发挥作用了。同时，应急电源为系统提供负荷供应时的移动规律需要好好把握才能达到好的恢复效果，目前常见的处理应急电源在交通系统中的移动主要有交通系统配流模型和迪杰斯特拉算法(Dijkstra)，本文主要采用的是更新了的Dijkstra算法，便于分析交通破坏对于应急电源移动规律的影响情况。

目前常见的可移动应急电源主要有电动汽车车队、车载移动储能系统和移动应急发电机。其中电动汽车车队和车载移动储能系统为电网供电时存在互动性，包含了充放电两个过程，电量会发生交换，而移动应急发电机则是单独为电网提供有功功率支撑。

可移动应急电源都具有灵活方便等特点，可以在不可预知的极端事件后及时方便地到达电力系统需要补给电力的节点，为系统补充电力，可以很好地提高系统的生存力与恢复力。另外应急电源的移动与其参与电力系统恢复的情况复杂，在此假设若某重要用户被提供移动应急电源，则认为移动应急电源为此用户提供足够长时间的电能。

考虑到灾害发生后系统会大面积失负荷，而应急电源的数量不能完全匹配时，需要对电源的接入情况进行优化，最大化地发挥全部应急电源的作用，尽可能地恢复更多更重要的负荷。如图1所示，图中展示了应急移动电源为重要用户提供电力进行配置的模型，供应点为其负责的重要用户配置应急电源。大停电时，供应点按照预先配置要求，派出能够满足重要用户电能容量需求的应急电源提供给重要客户。

Figure 1. Application model of emergency mobile power sources

图1. 应急移动电源应用模型

3. 可移动应急电源预置模型

自然灾害的突然袭来，不仅对电力系统造成破坏，同时也可能对交通系统造成破坏。当交通系统中道路遭到破坏时，必然也将影响应急电源移动路径及移动时间，需要同时考虑交通系统弹性，便于在道路遭遇破坏时最小化移动距离。交通系统中主要用到最短路径来研究车辆移动路径及移动时间，当已知系统中两个相邻相连节点之间的实际距离，可以通过最短路径来求出任意两个节点间的最短路径及距离，同时后续也会考虑道路遭遇破坏的情况。

极端灾害的突发性与破坏性要求电力系统需要拥有极强的生存力与抵抗力才能与之应对，文中针对灾害发生的不确定性采用了利用多个场景随机优化的方法，便于在不同类型的灾害突发时均能够从容应对，同时考虑道路破坏与线路破坏，让应急电源在极短时间内到达最佳指定位置，提高电力系统的生存抵抗力。

第一阶段应急电源预置部分大致思路框图如图2。

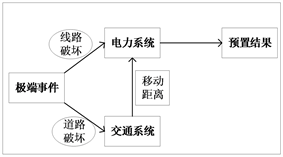
Figure 2. Research ideas and block diagram structure

图2. 研究思路及框图结构

3.1. 目标函数

电力系统弹性要求电力系统在极端事件发生后快速恢复重要负荷，应急电源的适时出现可以达到这一目标，与此同时应急电源的移动恢复也将受到极端事件下交通系统的约束即最短路径或最短距离。所以本文利用移动电源作为桥梁建立起一个针对多场景下电力–交通网破坏的应急电源预置模型，具体如下：

$\max {\displaystyle \underset{y\in Y}{\sum }{P}_y}\left({\displaystyle \underset{i\in I}{\sum }{\omega }_i{p}_{iy}-\gamma }{\displaystyle \underset{s\in S}{\sum }{\displaystyle \underset{q\in Q}{\sum }{\displaystyle \underset{i\in I}{\sum }{x}_{qiy}^s{d}_{qiy}^s}}}\right)$ (1)

该目标函数是指以多场景下最大化恢复电力系统负荷、最小化应急电源移动距离为目标。其中参数 $P_y$ 表示场景y发生的概率， ${\omega }_i$ 表示节点i的负荷权重，变量 $p_{iy}$ 表示场景y下负荷节点i的恢复负荷， $\gamma$ 表示考虑交通系统的权重系数， $x_{qiy}^s$ 为二元变量，当场景y下应急电源s从起点q移动到终点i时取值为1，否则为0。参数 $d_{qiy}^s$ 表示场景y下应急电源s从起点q移动到终点i的最短距离，其值是通过改进的Dijkstra算法求得，考虑了道路破坏使应急电源出行路径发生改变的情况。

3.2. 约束条件

应急电源安置位置约束：

${\displaystyle \underset{s\in S}{\sum }{x}_q^s\le X_q,\forall q}$ (2)

${\displaystyle \underset{q\in Q}{\sum }{x}_q^s}=1,\forall s$ (3)

${\displaystyle \underset{i\in I}{\sum }{x}_{qiy}^s\le 1,\forall q,\forall s,\forall y}$ (4)

${\displaystyle \underset{i\in I}{\sum }{x}_{qiy}^s\le x_q^s,\forall q,\forall s,\forall y}$ (5)

约束(2)表示安置在位置q的应急电源数量不超过位置q允许的安置容量，其中参数 $X_q$ 表示位置q允许安置的最大应急电源数目。 $x_q^s$ 为二元变量，当应急电源s安置在位置q时取值为1，否则为0。约束(3)表示一个应急电源只能安置在一个位置。约束(4)表示任一场景下应急电源只能从一个安置位置移动到一个负荷节点。约束(5)表示任一场景下从安置位置出发移动的应急电源数目应小于安置位置安置的电源数目。

电力系统节点功率平衡约束：

$P_{iy}+{\displaystyle \underset{g\in G_i}{\sum }{P}_{gy}+{\displaystyle \underset{\left(j,i\right)\in L}{\sum }{p}_{jiy}-}}{\displaystyle \underset{\left(i,j\right)\in L}{\sum }{p}_{ijy}}=p_{iy},\forall i,\forall y$ (6)

$Q_{iy}+{\displaystyle \underset{g\in G_i}{\sum }{Q}_{gy}+{\displaystyle \underset{\left(j,i\right)\in L}{\sum }{q}_{jiy}-}}{\displaystyle \underset{\left(i,j\right)\in L}{\sum }{q}_{ijy}}=q_{iy},\forall i,\forall y$ (7)

$0\le p_{iy}\le p_i^d,\forall i,\forall y$ (8)

$q_{iy}\le \left(\frac{q_i^d}{p_i^d}\right)p{}_{iy},\forall i,\forall y$ (9)

约束(6)表示任何场景下任何节点应满足有功功率平衡，变量 $p_{iy}$ 表示场景y下应急电源在节点i处的有功出力总和，变量 $P_{gy}$ 表示场景y下主网提供的有功功率大小，变量 $p_{ijy}$ 表示场景y下线路 $\left(i,j\right)$ 上流动的有功功率大小。约束(7)表示任何场景下任何节点应满足无功功率平衡，变量 $Q_{iy}$ 表示场景y下应急电源在节点i处提供的无功功率总和，变量 $Q_{gy}$ 表示场景y下主网提供的无功功率大小，变量 $q_{ijy}$ 表示场景y下线路 $\left(i,j\right)$ 上流动的无功功率大小。约束条件(8)表示节点i处恢复负荷总和应不超过节点i处的负荷总量，参数 $p_i^d$ 表示节点i处的负荷总量。约束条件(9)表示节点i处无功恢复量与该节点的有功恢复量及功率因数之间的关系，参数 $q_i^d$ 表示节点i处的无功需求量。

应急电源有功无功出力约束：

$0\le P_{iy}\le {\displaystyle \underset{s\in S}{\sum }{x}_{iy}^s{P}_{\max }^s},\forall i,\forall y$ (10)

$0\le Q_{iy}\le {\displaystyle \underset{s\in S}{\sum }{x}_{iy}^s{Q}_{\max }^s},\forall i,\forall y$ (11)

约束(10)表示应急电源的有功出力约束， $x_{iy}^s$ 为二元变量，场景y下应急电源s在节点i处出力时取值为1，否者为0，参数 $P_{\max }^s$ 表示应急电源s的有功出力上限值。约束(11)表示应急电源能提供的无功功率约束，参数 $Q_{\max }^s$ 表示应急电源s能提供的无功功率上限值。

线路交流潮流约束：

$p_{ijy}^2+q_{ijy}^2\le {\mu }_{ijy}{\left(s_{ij}^{\max }\right)}^2,\forall \left(i,j\right)\in L,\forall y$ (12)

$v_{iy}-v_{jy}\le \left(1-{\mu }_{ijy}\right)M_{ij}+2\left(r_{ij}{p}_{ijy}+x_{ij}{q}_{ijy}\right),\forall \left(i,j\right)\in L,\forall y$ (13)

$v_{iy}-v_{jy}\ge \left({\mu }_{ijy}-1\right)M_{ij}+2\left(r_{ij}{p}_{ijy}+x_{ij}{q}_{ijy}\right),\forall \left(i,j\right)\in L,\forall y$ (14)

${\left(v_i^{\min }\right)}^2\le v_{iy}\le {\left(v_i^{\max }\right)}^2,\forall i,\forall y$ (15)

约束(12)表示线路 $\left(i,j\right)$ 上流过的有功功率幅值平方与流过的无功功率平方和不超过该线路的视在功率的平方，其中参数 ${\mu }_{ijy}$ 表示线路 $\left(i,j\right)$ 在场景y下是否受损，其值为1时表示场景y下线路 $\left(i,j\right)$ 完整，其值为0时表示场景y下线路 $\left(i,j\right)$ 受损。参数 $s_{ij}^{\max }$ 表示线路 $\left(i,j\right)$ 的视在功率上限值。约束(13)表示基于DistFlow模型 [16] 的潮流方程，其中忽略了足够小的二次项，用一个足够大的整数 $M_{ij}$ 来对断开的线路约束进行松弛。其中变量 $v_{iy}$ 表示场景y下节点i处的电压幅值的平方， $r_{ij}$ 、 $x_{ij}$ 分别表示场景y下线路 $\left(i,j\right)$ 的电阻和电抗。约束(14)表示节点幅值平方的上下限约束。其中参数 $v_i^{\min }$ 、 $v_i^{\max }$ 分别表示节点i允许的电压幅值最小值和最大值。

上面便是完整的第一阶段多场景下应急电源的预置模型的数学形式，该模型为含有0-1变量的非线性规划模型，该模型用Python-gurobi编程求解。

4. 特定场景下应急电源实时调度模型

4.1. 目标函数

第一阶段的预置主要为提高电力系统的生存抵抗力，而在灾害实际发生时，需要及时地恢复，第二阶段主要为了增强电力系统的恢复力，相对于较长时间尽可能恢复更多更重要的复负荷，具体考虑实际灾害发生后短时间内应急电源参与电网恢复的实际情况，以第一阶段的预置结果作为调度部分电源的安置初始位置，建立一个弹性调度模型，以灾害发生后相对较长时间内系统失负荷量最小为目标，其目标函数如下：

$\min {\displaystyle \underset{t\in T}{\sum }{\displaystyle \underset{i\in I}{\sum }{\omega }_i}\left(p_{it}^d-p_{it}\right)t}$ (16)

该目标函数是以特定场景下灾害发生后系统短时间失负荷量最小为目标。其中参数 $p_{it}^d$ 表示时刻t节点i的负荷需求，变量 $p_{it}$ 表示时刻t节点i得到恢复的负荷，T表示所研究的时间尺度大小。

4.2. 约束条件

${\displaystyle \underset{i\in I}{\sum }{x}_{it}^s}\le 1,\forall s,\forall t$ (17)

${\displaystyle \underset{\tau =t+1}{\overset{\min \left(t+t_{qi}^s,T\right)}{\sum }}{x}_{q\tau }^s}\le \left(1-x_{it}^s\right)\min \left(t_{qi}^s,T-t\right),\forall s,\forall q\ne i,\forall t+1\le T$ (18)

约束(17)表示同一时刻一个电源只能接入到一个位置，其中 $x_{it}^s$ 为二元变量，其值为1时表示时刻t应急电源s接入到节点i。否则为0。约束(18)表示应急电源时刻位置与其在交通网中的移动时间关系。其中参数 $t_{qi}^s$ 表示电源s从节点q到节点i的时间。

电力系统节点功率平衡约束：

${\displaystyle \underset{g\in G_i}{\sum }{P}_{gt}}+P_{it}+{\displaystyle \underset{\left(j,i\right)\in L}{\sum }{p}_{jit}}-{\displaystyle \underset{\left(i,j\right)\in L}{\sum }{p}_{ijt}}=p_{it},\forall i,\forall t$ (19)

${\displaystyle \underset{g\in G_i}{\sum }{Q}_{gt}}+Q_{it}+{\displaystyle \underset{\left(j,i\right)\in L}{\sum }{q}_{jit}}-{\displaystyle \underset{\left(i,j\right)\in L}{\sum }{q}_{ijt}}=q_{it},\forall i,\forall t$ (20)

$0\le p_{it}\le p_{it}^d,\forall i,\forall t$ (21)

$q_{it}\le \left(\frac{q_{it}^d}{p_{it}^d}\right)p_{it},\forall i,\forall t$ (22)

约束(19)表示时刻t节点i的有功功率平衡。其中 $G_i$ 表示节点i上连接了主网g，变量 $P_{gt}$ 表示主网g在时刻t的出力，变量 $P_{it}$ 表示时刻t节点i上接入的应急电源提供的有功功率大小，变量 $p_{ijt}$ 表示时刻t上线路 $\left(i,j\right)$ 上流过的有功功率。约束(20)表示时刻t节点i的无功功率平衡。变量 $Q_{gt}$ 表示主网g在时刻t提供的无功功率，变量 $Q_{it}$ 表示时刻t节点i上接入的应急电源提供的无功功率大小，变量 $q_{ijt}$ 表示时刻t上线路 $\left(i,j\right)$ 上流过的无功功率。变量 $q_{it}$ 表示时刻t节点i上能恢复的无功功率大小。约束(21)表示时刻t节点i所能恢复的有功功率不超过该节点实际存在的负荷大小。约束(22)表示时刻t节点i所能恢复的无功功率与该时刻恢复的无功功率及功率因数之间的关系。其中参数 $q_{it}^d$ 表示时刻t节点i上实际存在的无功功率需求。

应急电源有功无功时刻出力约束：

$0\le P_{it}\le {\displaystyle \underset{s\in S}{\sum }{x}_{it}^s{P}_{\max }^s},\forall i,\forall t$ (23)

$0\le Q_{it}\le {\displaystyle \underset{s\in S}{\sum }{x}_{it}^s{Q}_{\max }^s},\forall i,\forall t$ (24)

约束(23)表示时刻t节点i接入电源提供有功功率的上下限约束。约束(24)表示时刻t节点i接入电源提供无功功率的上下限约束。

$p_{ijt}^2+q_{ijt}^2\le {\mu }_{ij}{\left(s_{ij}^{\max }\right)}^2,\forall \left(i,j\right)\in L,\forall t$ (25)

$v_{it}-v_{jt}\le \left(1-{\mu }_{ij}\right)M_{ij}+2\left(r_{ij}{p}_{ijt}+x_{ij}{q}_{ijt}\right),\forall \left(i,j\right)\in L,\forall t$ (26)

$v_{it}-v_{jt}\ge \left({\mu }_{ij}-1\right)M_{ij}+2\left(r_{ij}{p}_{ijt}+x_{ij}{q}_{ijt}\right),\forall \left(i,j\right)\in L,\forall t$ (27)

${\left(v_i^{\min }\right)}^2\le v_{it}\le {\left(v_i^{\max }\right)}^2,\forall i,\forall t$ (28)

约束(25)表示时刻t线路 $\left(i,j\right)$ 上流过的有功功率幅值平方与流过的无功功率平方和不超过该线路的视在功率的平方，其中参数 ${\mu }_{ij}$ 表示线路 $\left(i,j\right)$ 是否受损，其值为1时表示线路 $\left(i,j\right)$ 完整，其值为0时表示线路 $\left(i,j\right)$ 受损。约束(26)、(27)同约束(13)、(14)一样，分别表示时刻t下基于DistFlow模型的潮流约束以及节点电压幅值平方的上下限约束。其中变量 $v_{it}$ 表示时刻t下节点i电压幅值的平方。

5. 方法设计

5.1. 多场景法处理极端事件的不确定性

极端自然灾害具有很大的不确定性与高破坏性，本文在章节3预置模型中针对不确定性问题采用了多场景的方法来进行建模，通过对过往电力系统遭到破坏的历史数据进行统计，得到各种场景下线路遭到破坏的概率，模拟了各种破坏场景，通过对各种场景下的破坏情况进行分析计算，采用多场景的方法求出一个期望解，包括了多种场景下的电力系统破坏情况，避免了研究问题的偶然性，很好的解决了极端事件不确定问题。

多场景法在数学模型中的实现是设置了场景y作为变量的索引，不同的场景下会有不同的情况，来尽可能的模拟未知的极端事件，去最大化的减小极端事件带来的破坏。

5.2. 更新的Dijkstra算法

在预置模型中考虑了交通破坏后的应急电源最短出行距离影响应急电源参与电力系统恢复的效果，本文对道路破坏后的出行路径采用更新的Dijkstra算法来进行求解。

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。该算法用于求取图中指定两点之间的最短路径，或者是指定一点到其它所有点之间的最短路径，适用于边权为正的无向和有向图，不适用于有负边权的图。

当交通系统中某一条道路遭遇破坏而无法通行时意味着经过这条道路的所有路径将全部发生改变，需要绕道而行，出行最短距离也将发生改变。考虑到Dijkstra算法在处理不是直接相邻相连的道路(即没有实际距离可以标注的道路)时用的是距离无穷大来描述，所以这里可以也用道路距离无穷大来处理损坏道路的距离，这样就可以来分析道路破坏的交通系统出行规律来求出最短路径及最短距离。

系统道路遭到破坏的情况，道路破坏无法通行时应急电源移动路径将发生改变，本文将该破坏道路的实际距离当作无穷大处理，便于研究计算。基于上述理论，可以求出任意一种破坏场景下任意节点间的距离，为后续模型求解提供重要数据，该方法考虑了交通破坏对弹性恢复的影响。

6. 算例分析

6.1. 应急电源预置部分算例

本文的研究算例中电力系统为IEEE33节点系统，32条电力线路，五个联络开关，便于研究交通系统破坏对应急电源预置的影响，设计了对应的33节点交通系统，图3为电力/交通拓扑图。

电力系统节点负荷大小和电力系统线路参数为IEEE33节点数据，基准值取10MVA。交通系统道路长度在上图中标出，其值见附表A1。

选择了三台应急电源进行出力，其最大出力参数值如表1所示。

基于极端事件的不确定性，本文在设置参数时，随机生成位于1~10之间的负荷权重值，同时随机生成电力系统线路破坏情况，固定每个场景道路破坏情况(均以断掉三条道路为例)。设置了10个破坏场景，其场景参数的具体设置如下：

Figure 3. The diagram of power/transportation system

图3. 电力/交通系统拓扑示意图

Table 1. Maximum output value of emergency power sources

表1. 应急电源最大出力值

场景1：概率为0.1，道路(4, 5)、(2, 22)、(17, 18)破坏。

场景2：概率为0.1，道路(5, 6)、(12, 13)、(15, 16)破坏。

场景3：概率为0.05，道路(14, 15)、(18, 19)、(15, 20)破坏。

场景4：概率为0.15，道路(3, 4)、(8, 9)、(16, 29)破坏。

场景5：概率为0.1，道路(1, 2)、(19, 20)、(6, 26)破坏。

场景6：概率为0.15，道路(8, 9)、(9, 10)、(27, 28)破坏。

场景7：概率为0.05，道路(6, 7)、(11, 12)、(14, 20)破坏。

场景8：概率为0.1，道路(7, 8)、(14, 15)、(3, 23)破坏。

场景9：概率为0.1，道路(3, 4)、(10, 11)、(23, 28)破坏。

场景10：概率为0.1，道路(7, 8)、(11, 12)、(16, 17)破坏。

在模拟了300次之后得出预置及恢复结果如下：

其中预置结果如表2。

Table 2. Results of optimal configuration of emergency power sources

表2. 应急电源最优配置结果

恢复情况如图4和表3所示。

Figure 4. Recovery results considering traffic or not

图4. 考虑交通与否的恢复结果

Table 3. Simulation statistics for survived loads

表3. 存活负荷的统计分析表

图4为300次模拟之后的考虑交通出行与不考虑交通出行的恢复效果对比图，表3为模拟300次后得到的目标函数值的一些统计数据，由于随机产生的破坏场景，系统破坏程度的不同使目标值会出现一定的波动，最大值与最小值之间有一定的差距，但这刚好也反映了极端事件的不确定性，可以看到当不考虑交通系统的破坏情况时，恢复的负荷更多，但却忽略了极端事件带来的实际破坏情况，因此必须考虑应急电源的实际出行，该预置结果也验证了针对更多普遍破坏情况下都更具有效果。

本文共设置了10个场景，每个场景中道路、线路均遭到了不同程度的破坏，文中用了更新的Dijkstra算法来处理了道路破坏的情况，在随机生成负荷权重值与线路破坏条数的情况下进行模拟了300次随机模拟试验，该模型的结果输出可以实现在道路和线路完整和遭到不同程度破坏的所有场景下，利用有限的应急电源数量及出力来最快地最大化地恢复中断负荷，该结果是在10种场景下的加权最优值，即为多场景下应急电源的最优配置，起到了未知灾害到来时短时间内快速恢复重要负荷的作用，提高了电力系统生存抵抗力。

6.2. 应急电源实时调度算例

灾害实际发生后，应急电源被按照预定位置接入到电力系统参与负荷恢复，本文是以整体恢复最优为原则，该场景如图5所示：

Figure 5. Schematic diagram of power system failure

图5. 电力系统故障示意图

上图所示场景中5条线路遭到破坏，分别是线路(5, 6)、(2, 22)、(9, 10)、(15, 16)、(26, 27)。各个节点负荷权重值(见附录表A2)，固定应急电源出行时间，设置了T = 24时刻，根据日负荷曲线得到24时刻的负荷值，电源采用和第一阶段相同的三个应急电源型号和参数。

设置完相应参数之后，该模型通过在python-gurobi上编程求解得出结果，目标函数值为83273.7。其应急电源的实时调度如表4。

Table 4. Real-time dispatching results of emergency power sources

表4. 应急电源实时调度结果

表中分别描述了应急电源1~3在24个时刻的状态，“移动”表示该应急电源此时段正在移动过程中，节点编号表示应急电源此时段接入到该节点。

根据调度结果求出三个应急电源的各个时刻的出力情况如图6所示。

因为各个时刻的负荷情况不同，再结合负荷权重值，使得每个时刻应急电源接入电网的位置发生改变，应急电源恢复位置发生改变需要移动时间，考虑以上因素，模型求解后得到了上表中的调度结果。同时作为对照，这里设置了一个对照组进行比较，对照组中的应急电源不参与移动调度，应急电源的位置如表5。

Figure 6. Time output diagram of emergency power supply

图6. 应急电源时刻出力图

Table 5. Emergency power position table (control group)

表5. 应急电源位置表(对照组)

对照组的目标值与应急电源参与调度的目标值比较如表6。

Table 6. Comparison of results of dispatching emergency power supply or not

表6. 是否调度应急电源的结果对比

由表6可以看出，当应急电源参与调度，尽可能到达电力系统需要接入电源的位置进行恢复时的目标函数值更大，即使应急电源不参与调度时不需要发生移动而可以每个时刻都为系统出力，但目标值仍没有参与调度的结果好，所以所提方法效果较为更好，更能在灾害到来后恢复更多重要的负荷。

此外系统恢复与电源出力情况如图7所示。

Figure 7. The diagram of recovery load and power output

图7. 恢复负荷量与电源出力图

图7中描述了各个时刻的负荷恢复情况，电源出力包括了主网与应急电源同时出力，考虑到应急电源的费用相对比较昂贵，且应急电源是在主网不能满足电网时进行补给，所以可以看出主要还是主网在供电，应急电源的作用还是在相对比较更为重要的负荷点出力供电，很好发挥了其作用，明显地提高了电力系统的恢复力。

7. 结论与展望

本文主要结论和贡献如下：

1) 第一阶段考虑了道路和线路的双重破坏性，更好地反应较为真实实际的极端灾害，很好地应对了极端事件的不确定性与破坏性，应急电源的预置结果对于应对未知极端事件的到来、及时恢复重要负荷以及保证电力供应具有重要指导意义，最大化地提高了电力系统生存抵抗力。

2) 第二阶段考虑了应急电源在交通系统出行的时间与实时恢复位置的关系，得出了实际灾害到来时应急电源在每个时刻的实际最佳状态，调度电源让系统最大化地恢复了更多更重要的负荷，明显提高了电力系统的恢复力。

最后，当考虑实际交通系统破坏时，应急电源实时调度紧急恢复还有待研究，同时电力网络拓扑的变换和交通系统实时出行流量都将对灾后系统恢复产生影响，后续将继续研究。

参考文献

附录

Table A1. Road parameters of traffic lines

表A1. 交通系统道路参数

Table A2. Weights of power loads

表A2. 电力系统负荷权重