摘要:
大约一百多年前, Ramanujan 首次定义了经典的 Ramanujan 和:
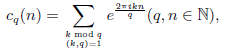
其中ℕ是正整数集. (k, q) 是 k 和 q 的最大公因子. 1976年, 在 Wintner 的结果的基础上, Delange 证明了定义在整数环ℤ上的单变量算术函数可以通过 Ramanujan 和加以展开. 2018 年, T´oth 证明了定义在ℤ上的多元算术函数可以通过 Ramanujan 和与酉 Ramanujan 和加以展开. 在此基础上, 本文试图将定义在代数整数环上的多元理想函数通过 Ramanujan 和加以展开, 同时也将进一步研究代数整数环上 Ramanujan 和的乘性与正交关系等性质.
Abstract:
One hundred years ago, Ramanujan first defined the following classic Ramanujan sum:
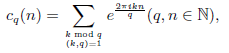
where ℕ is the set of positive integers, and (k, q) is the greatest common factor of k and q. In 1976, on the basis of Wintner’s results, Delange proved that all univariate arithmetic functions defined on the integer ring ℤ can be expanded by Ramanujan sum. In 2018, T´oth proved that the multivariate arithmetic function defined on ℤ can be expanded by Ramanujan sum and unitary Ramanujan sum. On this basis, this paper attempts to expand the multivariate ideal function defined on D through the Ramanujan sum. At the same time, it will further study the multiplicative and orthogonal relations of the Ramanujan sum on D.