1. 引言
深圳是我国水资源严重缺乏的城市之一,全市多年平均水资源总量18.72亿m3,按2017年末常住人口(1252.83万)计算,人均占有水资源量仅为157.24 m3,因境内无客水经过,且无太多适合修建大型水库的地形条件,深圳本地水资源可开发利用率很低,供水必须高度信赖于境外水源——东江流域的远距离输水来解决,2017年境外用水已超80%,未来预计将会更多。供水问题一直是制约深圳市经济发展的一个重要因素,并且随着经济的发展,城市规模的不断扩大,深圳市给水系统的供需矛盾将更加突出。因此,进行供水量的预测分析将为未来合理分配水资源提供重要的科学依据,并对深圳市供水规划和水务管理工作起着宏观指导作用。
城市供水系统是一个复杂的大系统,城市供水量不仅受当地水资源总量的影响,而且还与城市的社会经济发展、人均生活水平、供水设施建设、供水价格以及境外引水等众多因素有关。目前,城市供水量的预测方法主要有时间序列分析法 [1]、结构分析法 [2]、系统分析法 [3] 三种主要类型。采用不同的预测方法与模型,其结果也各不相同,有的甚至差别很大。近年来,组合预测(Combined Forecasting, CF)方法已成为预测领域中一个重要的研究方向,并引起了国内外众多学者的兴趣 [4] [5] [6]。理论上证明组合预测方法的效果优于选用的任何一种预测方法 [7]。由于可用多种预测方法对城市供水量进行预测,在将这些方法进行组合前,必须对单一预测方法进行选择。选择构成组合预测的预测方法应注意如下几点:首先,所选方法应大致适应预测对象与预测环境;其次,必须对各单一预测方法的预测性能优劣程度进行判别,在入选的诸多预测方法中至少应有一个具有优良性能的预测方法;最后,考虑到预测方法数目对最优组合预测性能的改变幅度呈现递减的趋势,构成预测方法总数目一般取2~5个即可取得较好的预测性能。因此,本文以深圳市供水量近二十多年的统计资料为基础 [8],应用文献 [9] 智能组合预测方法,依据线性回归 [10],非线性二元转折曲线 [11],模糊优选BP神经网络 [12] 预测模型,对深圳市未来的供水量进行了预测。线性回归法是根据供水量的多年平均值和相关性,递推求出下一年的供水量,反映的是年际供水量之间的线性相关;模糊优选BP神经网络法则是对简单的非线性函数进行数次复合从而近似复杂函数的能力。这3种模型建立的基础和考虑的因素都不尽相同,有着各自的适用性和不足之处。本文将这3种模型联立起来,得到的3个计算预测结果再作为模糊优选BP神经网络的3个输入节点值,并进行训练,其所得输出为最终的组合预测值。这里,将单一模拟因子通过技术手段变为多重预测因子,在模糊优选BP神经网络中进行训练,从而提高其预测精度与结果的稳定性。
2. 线性回归预测模型
模型形式为:
由最小二乘法估计参数a,b如下:为使
最小,可解极值方程
得方程组
(1)
记
,
(n年供水量的平均值,当前年份的n值为21)。
代入(a):
,代入(b):
由此得正规方程组
(2)
解出
(3)
可得到预测模型:
。
应用深圳市历年供水量统计数据表1 [13],可计算得到:a = 1806.6547,b = 1.0187。则线性回归预测模型为:
,预测结果(1981~2020年)及与实测值的误差见表2中3~4列。
3. 非线性二元转折曲线模型
通过分析表1中深圳市历年供水量时,很明显,其数据具有转折发展趋势,因此可以用非线性二元多项式转折预测建模 [10] [11],其模型形式为
(4)
式中:a,b,c为待估参数,由最小二乘法得到,k为按时序排列的供水量序号,由于从1981年开始预测,故当1981年时k = 1,1982年时k = 2,以此类推。设
(5)
为使Q最小,利用极值原理得:
,
,
(6)
从而得方程组
(7)

Table 1. Annual statistics of water supply of SSEZ
表1. 深圳市供水量历年统计表
将表1中的供水量数据代入式(7)中,可解得:a = 53.4,b = 1410.7,c = −1791.1。将这三项代入式(4)中,得非线性二元转折预测模型为:
,将相应的k值(
)代入该式并进行预测,其计算结果(1981~2020年)及与实测值的误差列于表2中5~6列。
4. 模糊优选BP神经网络预测模型
为了论述方便构造一个3层的模糊优选BP神经网络系统 [12],如图1所示。设输入层有m个输入节点,即有m个指标;隐含层有l个隐节点,即有l个单元系统;输出层有q个输出节点,即是有q个预测年份的最终相对隶属度,设有n个预测年份,对于预测年份j指标i的输入为
。这里将BP神经网络的隐含层与输出层的激励函数取为Sigmoid型的模糊优选模型 [12]。
在输入层节点i将输入信息(综合相对隶属度)直接传给隐含层节点,则节点输入与输出相等,即
。对隐含层的节点k,其输入输出的激励函数分别为
(8)
式中:
为输入层到隐含层的连接权重。对于输出层节点h,其输入、输出的激励函数分别为
(9)
式中:
为模糊优选BP神经网络输出层的输出值,也即所求预测年份的最终相对隶属度;
为隐含层到输出层的连接权重。
设预测年份j的期望输出为
,则其与实际输出
的平方误差为
(10)
由此可推出输入层节点i与隐含层节点k的权重调整量公式为 [13]
(11)
式中:
为学习效率,
由下式确定:
(12)
隐含层节点k与输出层节点h之间的权重调整量公式为
(13)
由此得到权重调整公式为
(14)
(15)
式中:t为迭代次数;
为动量系数,且
。
式(11)~(15)即是模糊优选BP神经网络权重调整模型。应用该模型,并根据通常神经网络的迭代算法,可确定网络连接权重值,使实际输出与期望的误差最小。
为方便计算,对表1中的数据进行标准化,由于供水量属于越大越优型,则可用公式 [9]
(16)
式(16)中,
为80~01年实测数据的最大值(即01年数值46,038),
为第t年实测数值,这样就将表1中的数据化为在[0 1]区间的标准型以利于Sigmoid函数计算,当BP循环输出结果大于实测最大值,即
时,令
。经试算,当模糊优选BP神经网络预测模型隐含层节点数为4个时所建模型具有较小的预测误差,因此本文取1-4-1结构的神经网络,即一个输入参数,为历年供水量,一个输出变量,即预测的下一年供水量值,隐含层节点4个。则用1980~1998的19组(0~1标准化后)实测值作为神经网络的输入值,用1981~1999年的19组(标准化后)实测值作为神经网络期望输出,网络训练误差为
,最大训练次数为20,000次,对神经网络进行训练,得到两权重矩阵(向量),再用此得到的已知权重矩阵(向量)检验2000、2001的预测值,预测结果(1981~2001年)及误差列于表2中7~8列(还原计算时将得到的位于[0 1]之间的预测数据乘以实测最大值46,038即得预测数列)。用线性回归得到的下一年供水量数据作为神经网络标准化的新的最大值及下一年期望输出值,重复上面的步骤,即可进行滚动延长预测(表2中第7列,为简单计表中只列出了2005、2010、2020三个年份的数据)。
5. 预测效果评价
为了检验各模型预测效果的好坏,按照预测效果评价原则和惯例,采用下列3项拟合误差指标作为评判准则,对预测效果进行全方位的综合性评价。
1) 均方误差
,其中
为预测年份实际值,
为预测值。
2) 平均绝对误差:
。
3) 平均绝对百分比误差:
。
6. 深圳市供水量智能组合预测
深圳市1980~2001年供水量历史数据已如表1所示,表中的供水量指关内四区罗湖、福田、南山、盐田(不包括关外宝安、龙岗两个区)的供水量。各单一预测模型与组合预测模型的预测结果一并列入表2中。
从表2可以看出3个单一预测模型各有优点,应该充分利用各个模型的有用信息。将上述3种预测模型计算得到的结果作为BP神经网络的输入值,选取3-4-1的网络结构,再次对3组数据进行训练。在输入神经网络时,仍然选用公式(16)并分别将三组预测值数据(1981~2001年)转化为[0 1]之间的数值,公式(16)相应地变为
(17)
式中:
仍用1981~2001年实测数据的最大值(即2001年数值46,038),
即用第t年相应方法的预测值,
为第t年相应方法的标准化值,
,
。对于BP循环当输入与输出
时,都令
。这样,将1981~1999年三组预测数据(0~1标准化后)作为该3-4-1型神经网络的输入值,用1981~1999年实测数据标准化数列作为网络期望输出,对该网络进行训练,最大训练次数为20,000次,网络结束条件为
,其中
与
分别为智能组合输出相应年份标准化后(0~1区间)的预测值与实测值,还原计算时仍然将得到的位于[0 1]之间的组合预测数据乘以实测最大值46,038得到预测数列。由此得到输入层到隐含层及隐含层到输出层的权重矩阵(向量)如下(未归一化):
,
将得到的两权重矩阵(向量)对2000、2001年实测数据进行检验。从表2中9~10列1981~2001年预测值及误差来看,该网络基本满足预测要求。再利用该网络两权重矩阵(向量)及三个单一预测值得出的延长预测值,就可以对深圳市供水量进行训练,最终预测值数列如表2第9列所示(表中只对应列出2005、2010、2020三个年份的值,其他数据可依此类推)。

Table 2. Forecasting results of water supply of SSEZ (unit: 104 m3)
表2. 深圳市供水量预测值(单位:万m3)
根据表2预测结果可见,无论从哪种预测性能指标进行评价,智能组合预测的预测效果都要优于任意一种单一预测模型,能提高模型的拟合精度和预测能力。供水量的智能组合预测模型可以综合多种供水量预测方法所提供的有用信息,使考虑的因素更加全面,因而,较供水量单一预测模型预测结果而言,它具有更好的科学性和通用性。特别是当不同预测模型得出的预测结果差别较大时,用模糊优选BP神经网络对结果进行智能组合预测能提高预测结果的稳健性。
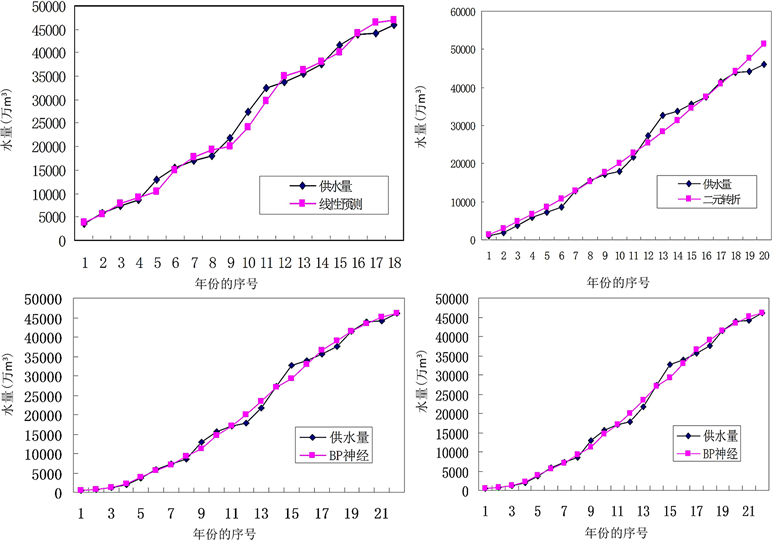
Figure 2. Fitting curve of forecasting model for water supply of SSEZ
图2. 深圳市供水量预测模型拟合曲线图
在图2中,纵坐标均为供水量预测值,横坐标为供水预测年份序号,1981年序号为1,以次类推。从图2中的四个小图都可以直观看出,深圳市供水量并不随时间推移线性增加,而是呈近似Losgistic曲线的增长方式:从1980年起,市供水量大致经历了从“缓慢增加”到“迅速增加”再到“缓慢增加”的过程,并在某些年份有较大波动,该过程与深圳市的历史发展情况相一致。而从四个拟合图形对比来看,二元转折没有线性回归好,模糊优选BP神经网络又比这二者的拟合精度高,3者的组合智能预测又优于任一单一预测方法,这从四者的平均绝对百分比误差也可以得出。综合来看,组合预测的预测精度基本上可以满足供水量的预测要求。此外,还必须针对未来城市发展可能出现的各种情况,结合结构分析法和系统分析法等多种预测方法所得的结果进行供水量综合模拟分析,建立由多种单一模型构成的供水量组合预测与模拟模型,以便更准确地预测未来供水量的变化,从而制定较合理的供水政策和供水管理措施。
7. 结语
这里主要是利用三种时间序列分析法进行组合预测深圳市供水量,所需数据只是市历年供水量一项指标,因而模型简单,操作方便,具有一定的实用性。然而,由于建立在时间序列分析法上的智能预测模型仅以历史数据的变化规律来外推未来的供水量,把影响城市供水量的所有因素都归结为“时间”这一个变量上,因此,严格说来,它是一种模拟模型,即只是对城市未来供水量的一种模拟分析,当城市发展不稳定,变化较剧烈,或某年降雨量异常,对特定年份的供水量预测与模拟误差可能较大。另外,由于它是完全基于时间这一变量的“黑箱模型”,不利于分析影响水量的主要因素。对于未来中远期预测,由于供水量的逐年增长、越来越大的特殊性,在没有实测数据对BP神经网络进行检验时,只有依靠其他方法(本文取线性回归)得到未来年份的期望值,由此带来的误差积累是一个相当棘手的问题,而发展出一种更好更高效的、适应这种外沿逐渐扩大的数据的预测方法,将是作者下一步的研究重点。
参考文献