三维扫描振镜动态聚焦控制系统建模与仿真

Modeling and Simulation of Dynamic Focusing Control System for 3D Scanning Galvanometer

摘要: 三维扫描振镜动态聚焦系统是激光三维加工的核心部件，动态聚焦系统实时补偿离焦误差的出现克服了传统二维扫描系统由于扫描范围增大，光程差存在导致聚焦面为球面且聚焦光斑不均匀性和不能加工三维立体表面等现象。目前市场上的动态聚焦控制系统研究较少，且大都存在着速度慢、响应慢和精度低等缺陷，不能满足新型行业及高端领域的应用需求。本文针对扫描式激光振镜打标系统平台设计了动态聚焦控制系统，首先基于电机平衡方程建立双电机的动力学数学模型；其次在电机模型基础上添加电流环、速度环、位置环三闭环PID控制并采构建动态聚焦控制系统simulink仿真模型；最后应用仿真模型对实际电机性能进行1%阶跃响应以及正弦跟踪响应验证，控制仿真模型与实际控制系统匹配度较好，满足三维高速激光加工需求，为高速高响应动态聚焦控制系统的控制性能研究提供了新的思路。

Abstract: The dynamic focusing system of three-dimensional scanning galvanometer is the core component of laser three-dimensional processing. The dynamic focusing system compensates the defocusing error in real time, which overcomes the phenomenon that the traditional two-dimensional scanning system has spherical focus surface and uneven focus spot due to the increase of scanning range and optical path difference. There are few researches on dynamic focusing control system in domestic market, and most of them have the defects of slow speed, slow response and low precision, which cannot meet the application needs of new industries and high-end fields. In this paper, the dynamic focusing control system is developed for the scanning laser galvanometer marking system platform. Firstly, the dynamic mathematical model of the double motor is established based on the motor balance equation. Secondly, the current loop, speed loop and position loop PID control are added to the motor model, and the Simulink simulation model of the dynamic focusing control system is built. Finally, the simulation model is applied to the actual motor. It can verify the 1% step response and sinusoidal tracking response, and the control simulation model matches well with the actual control system, which meets the requirements of 3D high-speed laser processing. It provides a new idea for the control performance research of high-speed and high response dynamic focusing control system.

1. 引言

三维动态聚焦系统可以适用于激光钻孔、切割、焊接以及微观结构制造等各个激光加工领域 [1]，目前市场上的应用多采用国外的高性能动态聚焦系统，国内对动态聚焦系统的研究多放在应用扩展上，如将动态聚焦系统配合扫描振镜对三维表面进行激光改性 [2]，利用动态聚焦系统补偿聚焦误差的方法，将其应用在激光选区熔化成形设备 [3]，其重点都不在于对动态聚焦系统的控制，而只是作为应用工具来实现应用的目的。对现有的动态聚焦系统研究总结发现目前存在一些问题 [4] [5]：1) 国内在三维动态聚焦控制系统性能研究还处于发展阶段，主要以工业上的中低端应用为主，高端领域还是依赖于进口，而相应的高速高响应动态聚焦系统控制方法开发与控制性能研究却较为匮乏；2) 未将动态聚焦系统同整个三维振镜扫描加工系统结合起来研究其控制性能。

本文将对某国产三维扫描振镜动态聚焦系统进行研究，通过建立驱动电机的动力学数学建模，扫描电机三环控制系统Simulink仿真模型与实际电机控制系统性能的匹配，通过进行三维加工测试不同焦深下的线宽，实现高速高响应的动态聚焦系统控制。对于动态聚焦系统控制的开发与提高系统控制性能研究提供了新的理论基础和研究思路。

2. 动态聚焦控制系统

2.1. 驱动电机数学模型建立

作为动态聚焦系统的核心部件驱动电机必须具备优良的动态特性，其电机的反应速度直接决定了动态聚焦镜的移动速度，同时需保证电机转动到任意位置时都有相同的动态特性。驱动电机与振镜电机相似都为动磁式电机，属于惯量低、转矩大、频率宽特殊型摆动电机一类 [4]，本次设计运用摇杆滑块机构加上加直线导轨带动变焦透镜如图1所示，其结构简单大大简化了控制方式，随着电机的摆动，实时改变扩束镜和聚焦物镜之间的距离来实现补偿因光程差△S造成的离焦误差，如图2所示，使得远离远点的激光束的光斑直径再次与远点的光斑达到一样大，确保扫描平面上的聚焦准确性。

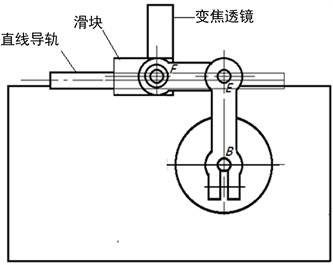
Figure 1. Rocker slider drive control diagram

图1. 摇杆滑块驱动控制简图

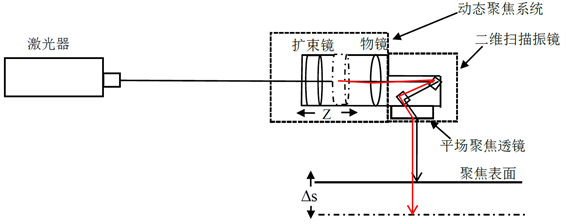
Figure 2. Schematic diagram of light path

图2. 光路原理图

建立动磁式电机的数学模型，其转动力矩计算公式为 [6]：

$T=T=B{L}_{r}NI{D}_r-2\pi {10}^{-7}M{L}_r{N}^2{I}^2\frac{D_r}{v}$ (1)

式中：T——转矩；B——永磁铁在空气隙中产生的磁感应强度；L_r——转子的长度；D_r——转子的直径；v——空气隙的间距；N——线圈匝数；I——线圈电流；M——转子最大转角与 $\alpha$ 角之比，在式(1)中，要尽量减小非线性项，提高系统的稳定性与速度。

由于扫描电机非线性项远小于线性项，因此进行理论分析与设计时，可将式(1)简化为：

$T=B{L}_{r}NI{D}_r{K}_{T}I$ (2)

式中 $B{L}_{r}NI{D}_r$ 对于确定的振镜电机是一个定值，故可令 $K_T=B{L}_{r}N{D}_r$，称为电机转矩系数，则上式可进一步简化为：

$T=K_{T}I$ (3)

由此可得电机转动力矩与线圈电流成正比，由转子负载图，应用牛顿第二定律，得出电机的转矩平衡方程：

$T=J\frac{{\text{d}}^2\theta }{\text{d}{t}^2}+f_b\frac{\text{d}\theta }{\text{d}t}+g\theta B{L}_{r}NI{D}_r{K}_T$ (4)

式中：T——电机线圈电流产生的电磁转矩；J——电机转子与轴上负载相对于电机转轴的转动惯量之和；

$\theta$ ——电机转子偏转速度； $\frac{\text{d}\theta }{\text{d}t}$ ——转子角速度； $\frac{{\text{d}}^2\theta }{\text{d}{t}^2}$ ——转子角加速度； $f_b$ 电机轴上粘性摩擦系数，

g——弹性系数，动磁式电机为零。

电机的电枢平衡方程：

$E_i=RI+L\frac{\text{d}I}{\text{d}t}+E_b$ (5)

$E_b=K_b\frac{\text{d}\theta }{\text{d}t}$ (6)

式中：R——电枢电阻；L——电枢电感；K_b——反电动势系数。

将式(3)至(5)联立，得到 $\theta$ 与 $E_i$ 之间的关系式：

$JL\frac{{\text{d}}^3\theta }{\text{d}{t}^3}+\left(JR+f_{b}L\right)\frac{{\text{d}}^2\theta }{\text{d}{t}^2}+\left(f_{b}R+gL+K_T{K}_b\right)\frac{\text{d}\theta }{\text{d}t}+gR\theta =K_T{E}_i$ (7)

将上式进行拉氏变换，整理后得到：

$G=\frac{\theta \left(s\right)}{E_i\left(s\right)}=\frac{K_T}{\left(Ls+R\right)\left(J{s}^2+f_{b}s+g\right)+K_T{K}_{b}s}$ (8)

此为电机的传递函数，由传递函数可得其是一个三阶系统，由于线圈电感L很小，与电阻R相比可以忽略，故传递函数简化为：

$G=\frac{\theta \left(s\right)}{E_i\left(s\right)}=\frac{K_T/R}{\left(J{s}^2+f_{b}s+g\right)+K_T{K}_{b}s/R}$ (9)

因此电机的实际工作状态近似为二阶系统，传递函数结构如图3所示：

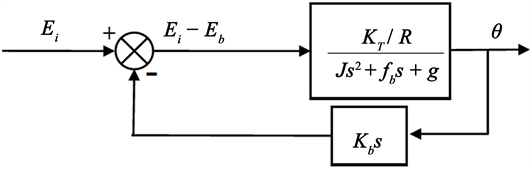
Figure 3. Structure diagram of transfer function of drive motor

图3. 驱动电机传递函数结构图

2.2. 动态聚焦控制系统建模

整个三维扫描振镜动态聚焦系统如图4所示，激光束先进入扩束镜片，再进入聚焦镜片组，然后经过XY扫描振镜的反射，最后才到达焦平面，利用一个传动装置沿光轴方向移动扩束镜片，将会改变扩束镜片与聚焦镜片组之间的距离，从而可以再在二维或三维空间内改变聚焦光点的位置，称之为“三维扫描”。

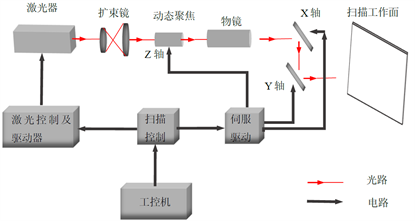
Figure 4. Structure diagram of dynamic focusing system for 3D scanning galvanometer

图4. 三维扫描振镜动态聚焦系统结构图

本文中动态聚焦控制系统仿真模型采用负反馈控制来建立闭环伺服控制系统，电机控制器结构图如下：

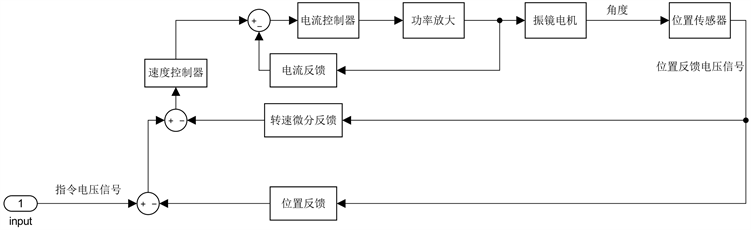
Figure 5. Structure diagram of motor controller

图5. 电机控制器结构图

三闭环控制系统 [7]，如图5所示，包括电流、速度、位置，依次从内向外组成串级控制结构 [8]，控制系统输出的是电机的偏转角度，偏转角度对应着扩束镜的位移及焦点的移动距离。电机的控制中则采取了PI控制和PID控制 [9]，速度环和电流环作为两个副回路采用PI控制器，能够有效的减少环路内部的干扰。位置环采用PID控制，加入微分结构以提高系统的稳定性。根据三环控制结构和电机简化模型得出控制系统模型 [10]，如图6所示：

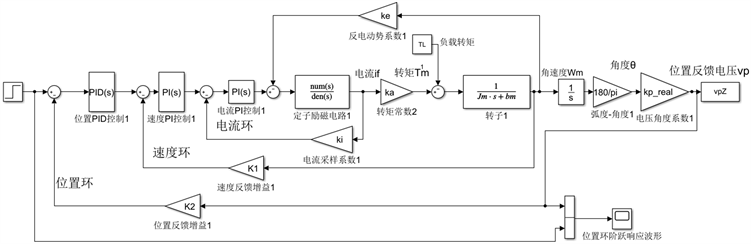
Figure 6. Control system simulation model

图6. 控制系统仿真模型

3. 实验性能分析与平台测试

在三维扫描振镜动态聚焦控制系统控制性能指标是以其位置环的阶跃响应时间来评判的。通过LabVIEW控制NI数据采集卡输出幅值为0.1 V方波信号，进行1%阶跃响应测试，截取测试所得信号的上升段，得到真实系统的阶跃响应。将其中的阶跃信号作为Simulink仿真模型的输入指令信号，通过将1%阶跃响应的试验结果与仿真结果进行对比(图7与图8)，可发现传统国产电机阶跃响应上升时间大约为3.35 ms，采用新型驱动器以及驱动电机的阶跃响应上升时间为2.1 ms，提升了59.5%。

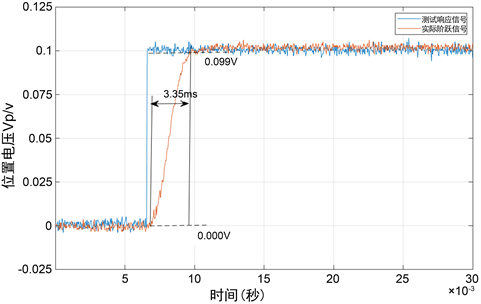
Figure 7. 1% step response of traditional domestic motor

图7. 传统国产电机1%阶跃响应

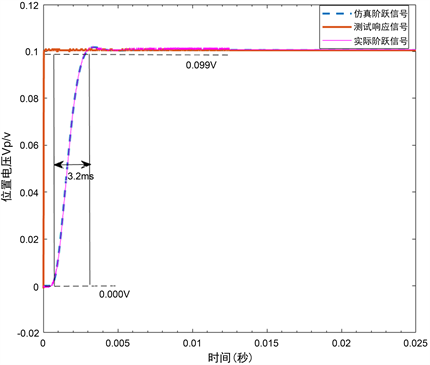
Figure 8. 1% step response of new drive motor

图8. 新型驱动电机1%阶跃响应

图8除了小步阶响应速度的提升还可以看出实际跟踪信号与仿真跟踪信号基本重合，性能的提升还需保证驱动电机的动态跟随能力，输入1 v正弦信号，并截取两个周期的输入信号与跟踪信号，如图9所示：

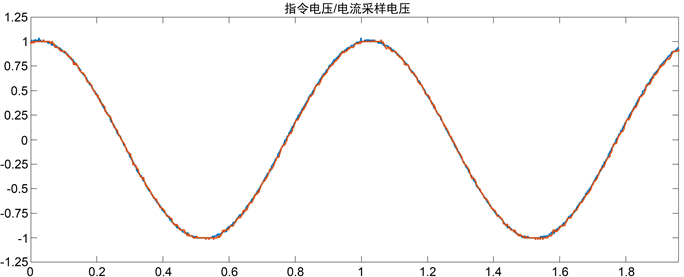
Figure 9. Sinusoidal tracking response of driving motor

图9. 驱动电机正弦跟踪响应

由实际输出信号与仿真输出信号得到两者间的误差，并以电机角度表示。误差曲线如图10所示，由图可知电机的正弦跟随误差在±0.03 V左右，有3%的误差，在可接受范围内，电机Simulink仿真模型与实际双电机控制系统匹配良好，能一定程度上代替实际系统进行研究分析，实现高速高动态响应的要求。

Figure 10. Sinusoidal tracking error curve

图10. 正弦跟踪误差曲线

4. 三维扫描加工平台测试

激光三维打标系统作为动态聚焦最基础也最简单的应用，将动态聚焦系统同整个三维振镜扫描加工系统结合起来研究其控制性能，在45度斜面放置120 mm × 80 mm铝片进行直径25 mm圆形打标，焦深为18 mm，其中打标速度1000 mm/s，通过打标系统的圆的各点线宽来研究动态聚焦控制系统的可行性，通过已有的实验平台采用基于CCD相机的机器视觉 [11] 来检测打标圆的线宽，通过其自带的测量软件可以测出斜面圆的顶部和底部线宽如图11所示。

由图11可知斜面圆的顶部线宽为0.0496 mm，底部线宽为0.0537 mm，误差基本在0.006 mm左右，经过多组数据其光斑大小的浮动范围在20%以内，符合要求。由此可得出结论：本文在新型驱动器下设计简化机械结构，建立了动态聚焦控制系统仿真模型，与实际动态聚焦控制系统较为匹配，提升性能的同时控制了加工边界处的光斑大小，满足实际三维扫描加工需求。

Figure 11. Line width measurement diagram

图11. 线宽测量图

5. 结论

本文以国产电机为研究对象，建立了三维扫描振镜动态聚焦控制系统，设计简便的机械机构，克服了其传统电机速度慢响应慢的缺点，并建立了完善的simulink仿真模型。提高了小步阶响应以及正弦跟踪响应，通过实验验证，在45度斜面进行打标，在不同焦深处的线宽误差较小符合要求。总体来说，此三维动态聚焦电机控制系统仿真模型具有较好的准确性，在一定程度上对于动态聚焦系统控制的开发与提高系统控制性能研究提供了新的理论基础和研究思路。

NOTES

^*通讯作者。