1. 引言
随着社会的发展使得汽车需求量急剧增加,缺乏驾驶经验的人群队伍日益壮大,当前社会对交通安全问题关注度越来越高,因此,积极推广智能小车自动避障系统的应用,有利于缓解道路交通拥堵和预防交通事故的发生 [1]。
目前,国内外提出的用于避障控制算法的传统模型有人工势场法 [2] 和虚拟力场法 [3] 等,上述方法存在精度低、计算速度慢、对于非线性映射的处理能力不理想等问题。支持向量机 [4] (support vector machine, SVM)模型具有较强的计算能力,能降低计算的复杂性,解决了小样本和高维数等问题,并且有优秀的泛化能力,但存在对于大规模样本训练以及多分类精度低等问题,并且还对参数和核函数选择敏感,核函数必须满足特定的Mercer条件 [5] [6] [7] [8]。反向传播人工神经网络 [9] (back propagation artificial neural network, BP-ANN)不仅具有强大的并行能力和自学习,而且还可以执行复杂的非线性映射,但其网络算法的收敛速度慢,在大规模网络模型中处理历史数据的能力较低,对于处理网络样本依赖问题存在较大困难 [10]。
脉冲神经网络(spiking neural network, SNN)即第三代神经网络 [11],为进行信息的传递和计算,其采用时间编码的方式将信息编码成脉冲序列形式,这种编码方式从信息的时间、空间以及频率等多方面进行融合,与其他类型的利用频率编码的神经网络相比,脉冲神经网络可以作为更复杂的信息处理工具。脉冲神经网络利用神经元的脉冲发放时间作为网络模型的输入和输出,不仅可以保证信息在传送过程中的完整性,而且能使网络拥有更强大的计算能力,实现了信息处理的高效性和完整性 [12]。而且脉冲发放时间只与神经元的输入有关,与脉冲的形状和大小无关,可以模拟任意连续函数和各种神经信号,使网络模型具有更强大的生物仿真性能 [13]。因此,本文建立基于脉冲神经网络的智能小车避障控制模型,并证明了该模型的适用性和有效性。
2. 网络训练算法与神经网络结构
脉冲神经网络框架大致由神经信息编码、神经元模型、训练算法以及网络结构组成,如图1所示。

Figure 1. Spiking neuron network framework
图1. 脉冲神经元网络框架
对于脉冲神经网络而言,其基本组成单元是脉冲神经元模型,其模型选用泄露积分点火模型 [14] (leaky integrate and fired model, LIF),LIF神经元工作原理简单,神经元的状态直接受输入信号的影响,当膜电位到达阈值电位时,神经元就会产生一个脉冲信号,随即神经元进入超极化状态和不应期状态,处在不应期状态下的神经元不受环境的影响,保持静息电位,直至进入下一个周期 [15] [16]。
2.1. 编码方式
由于信息在脉冲神经网络中传递的形式是脉冲序列,无法直接将数据信息传入网络中处理,因此,我们还需要对数据信息进行编码转换为脉冲序列。泊松编码机制 [17] 不仅相对其它编码机制来说其操作更为简单,处理速度更快,而且基于泊松编码的脉冲特别适用于STDP机制 [18]。泊松编码公式如下:
(1)
每个输入变量对应的输入神经元发放的脉冲个数成泊松分布,其中n是激发脉冲的个数,rt为与输入变量值成正比的激发频率,t时间内未产生脉冲的概率为
。
2.2. 网络训练算法
网络训练算法采用无监督学习方法——脉冲时间依赖可塑性机制,简称STDP学习规则。突触前神经元i与突触后神经元j建立一个神经连接,其突触权重为
,STDP学习规则认为,在一个时间窗口内,若突触前神经元i被激活后,突触后神经元j很快被激活,说明神经元i和神经元j之间具备紧密先后关系,则增强这两者之间的联系,即
增大;若突触后神经元j被激活后,突触前神经元i才被激活,说明神经元i和神经元j之间具备相反关系,则降低神经元i与神经元j之间的联系,即
减弱 [19]。其模型公式如下:
(2)
其中,
,
表示突触后神经元被激活的时间,
表示突触前神经元被激活的时间;
为神经元之间的突触权重的变化,
与
突触权重变化的最大值,均大于0,
和
为不同神经元模型的时间常量。
若
,则突触前神经元i到突触前神经元j之间的连接强度增加,反之则降低。
2.3. 脉冲神经网络结构
一般根据网络结构是否改变可将脉冲神经网络分为静态脉冲神经网络和动态脉冲神经网络,静态脉冲神经网络是指在训练过程中只改变权重等参数,不改变网络中的神经元数量和层数;动态脉冲神经网络不仅在训练过程中权重的改变,神经元数量和连接方式也存在动态调整 [20] [21]。本文采用前馈型全连接脉冲神经网络,网络结构如图2所示。由于网络结构采用的是无监督学习规则进行学习,所以引入抑制层进行竞争,这样可以让获胜神经元的权重增加,而其它神经元的权重减少,能够有效的降低训练过程中的噪声,得到更好的训练效果。
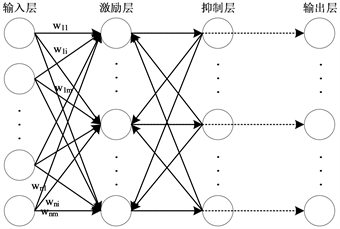
Figure 2. Full connection STDP spiking neuron model structure
图2. 全连接STDP脉冲神经元结构
输入层神经元数量为n,激励层神经元数量与抑制层神经元数量相等,均为m。在传统的全连接STDP网络结构中输入层神经元与激励层神经元之间采用全连接方式,激励层神经元与抑制层神经元采用一对一连接方式,为了构建一种竞争机制,将抑制层神经元与激励层的其他神经元进行一对多连接,激励层神经元与输出层神经元是一对一的方式进行连接。
但在上述全连接网络中,每一个突触都基于STDP规则更新权重,会导致计算量呈指数型增加。为了减少网络的计算量,本文提出了一种基于STDP规则的稀疏概率连接的网络结构,其连接示意图如图3:
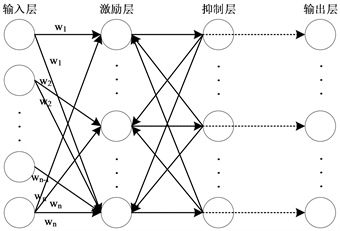
Figure 3. STDP spiking neuron network structures with sparse probability connections
图3. 基于STDP规则的稀疏概率连接的脉冲神经元网络结构
将输入层与激励层的连接权重设置为同一个值,权重值如下:
, (3)
同时将输入层与激励层之间的连接概率进行更改,令
(4)
其中
表示第k个输入层神经元与第i个激励层神经元连接的概率,s表示激励层神经元发放的脉冲数量,n表示输入层神经元数量;
为调节参数,其表示方式是:
(5)
其中
表示在全连接状态下通过一串驱动信号Q得到的激励层脉冲数量,Q的表示方式是:
(6)
网络连接概率的训练流程图如图4所示:
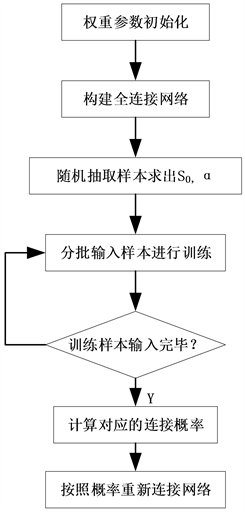
Figure 4. Flow chart of network connection probability
图4. 网络连接概率流程图
通过多次实验得出网络连接概率为0.5时,网络计算效率最佳。
3. 基于SNN的小车自动避障控制模型
3.1. 避障控制设计模型
脉冲神经网络的输入由小车当前的车速,小车当前时间分别与障碍物和目标点的距离以及小车与目标点之间的夹角这四个部分构成 [22]。结合COOPELIASIM软件和MATLAB软件,可以通过在小车身上安装三个超声波传感器如图5所示,来获取小车与左方、前方和右方的障碍物之间的距离D1~D3、小车前方与目标点的距离D4,通过计算可得小车与目标点之间的角度
、小车当前的车速v以及小车左轮与右轮的速度,利用小车左右的轮速差来实现自动避障的行为,如图6所示。
小车在行驶过程中左轮和右轮的速度计算公式如下:
(7)
式中:v代表小车的运行速度,w代表运行的角速度,D表示常量,根据公式(7)可知,影响车轮转动速度的主要因素是小车当前的运行速度以及角速度等。
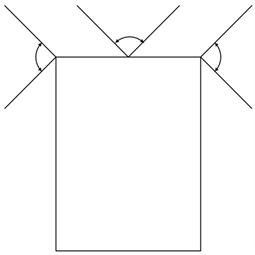
Figure 5. Sensors mounted distribution
图5. 传感器安装分布图
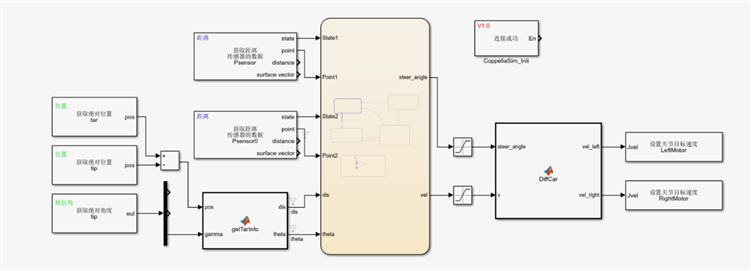
Figure 6. Obstacle avoidance controller settings
图6. 避障控制器设置
下图7是基于脉冲神经网络的避障控制设计模型。
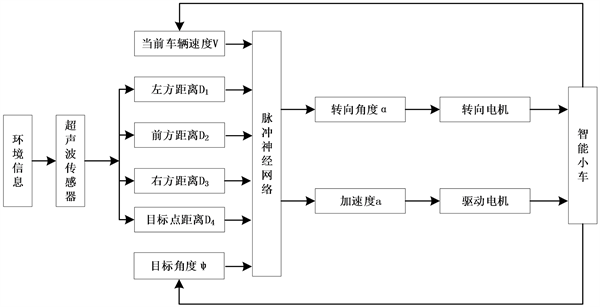
Figure 7. Model of obstacle avoidance based on spike neural network
图7. 基于脉冲神经网络的自动避障模型
3.2. 避障模型的相似路况选取
本文采用灰色关联分析法 [23] 确定与测试样本路况最接近的训练样本,具体步骤如下。
步骤1 本文的避障模型数据采用每间隔10 s采集小车当前的运行路况,为了更准确地选取相似路况,在构造路况特征向量时,统计训练样本中与采取避障行为数据相对应的不同时刻的路况信息作为初步样本,即传感器分别测得的小车与障碍物和目标点的距离、小车当前的车速以及小车与目标点之间的角度,即
(8)
(9)
(10)
(11)
(12)
其中:
为第i个训练数据样本中第j时刻小车所处的历史路况集合。
表示第i个训练数据样本中第j时刻传感器测得的小车与障碍物之间的距离特征向量;
为第i个训练数据样本中第j时刻传感器测得的小车与目标点之间的距离特征向量;
为第i个训练数据样本中第j时刻小车当前的车速特征向量;
为第i个训练数据样本中第j时刻小车与目标点之间的角度。
步骤2 为减少数据指标之间量纲的影响,对路况特征向量进行标准化处理,公式为:
(13)
其中:
为第i个历史路况数据样本中第j时刻的第k个路况特征分量,
和
分别为第i个历史路况数据样本中第k个路况特征分量的最大值和最小值。
步骤3 计算测试路况数据样本和第i个历史路况数据样本中第k个路况特征分量的关联系数为
(14)
其中:
为标准化后测试路况数据样本中第k个路况特征分量,
为标准化后的第i个历史路况数据样本中第k个路况特征分量;
为常量,本文选取0.6。
步骤4 为计算第i个历史路况数据样本和测试路况数据样本的总关联度R,按照历史路况的时间顺序排列,取
时靠近测试路况数据样本的第b个历史路况,本文b = 2。
(15)
其中:u为路况特征向量的分量个数。
3.3. 神经元个数的确定
小车在行进过程中,在一分钟内每隔10 s收集一次路况信息的数据量作为网络模型输入层神经元的个数,通过模型计算处理得到的信息数据量作为输出层神经元的个数,即传感器在一分钟内不同时刻收集的距离数据,再通过计算出得当前小车的速度以及与目标点的角度等数据量作为输入层神经元的个数,同时通过模型计算得到的小车的加速度和转向角度等数据量作为输出层神经元的个数。
由图2可知,激励层神经元与抑制层神经元个数相等,由于激励层神经元与输出层神经元是一对一连接,所以激励层神经元个数与输出层神经元个数也相等。
3.4. 基于SNN的小车自动避障控制方法流程图
综上所述,下图8是基于SNN的小车避障方法流程图。
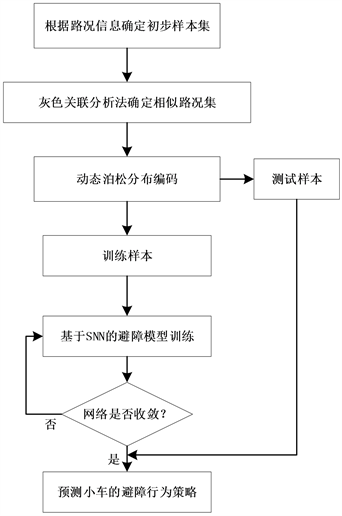
Figure 8. SNN-based obstacle avoidance method process
图8. 避障方法流程
4. 仿真实验
为了验证本文提出的基于SNN智能小车自动避障算法模型的有效性和准确性,结合COOPELIASIM、MATLAB(R2019b)和NEST软件作为仿真平台,以PYTHON3.6为编程环境编制了模拟仿真实验程序,来测试智能小车的避障行为的可行性。记录5组在一分钟内每隔10 s通过超声波传感器采集的距离数据计算得出小车当前的车速以及小车距离目标点的角度作为初步样本数据。分别采用SNN、SVM [24]、BP-ANN三种模型对样本数据中的小车偏转角进行计算预估,并记录相同路况条件下,采用这三种模型的小车的行驶轨迹。为控制变量,在用上述三种网络模型训练时,其相似路况的选取方法均采用灰色关联分析法。
4.1. 相关参数的设定
为了使网络结构的生物意义存在合理性,本文在模拟实验中设置的参数均在合理范围内。本文在根据文献 [25] 中关于网络参数的设定,并结合小车避障行为的相关特点,经过多次实验获得最佳避障行为的参数。如下表1所示:

Table 1. Optimum structural parameters of different network models
表1. 不同网络模型的最优结构参数
4.2. 仿真结果及分析
4.2.1. 小车行驶轨迹结果分析
如图9中,在障碍物分布较为稀疏的条件下,通过这三种避障模型训练后输出的结果使小车采取避障的行为是比较接近的。当增加障碍物的数量和分布密度时,如下图10所示,SNN模型和BP-ANN模型获得的结果几乎无太大变化,而采用SVM模型的小车行驶轨迹出现了大幅度变化。因此,SNN网络模型相对SVM模型其更具有适应性和稳定性。
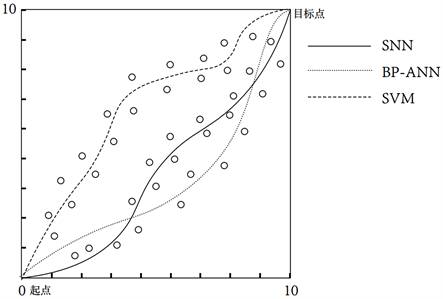
Figure 9. Vehicle trajectory under different network models
图9. 不同网络模型下的小车运行轨迹
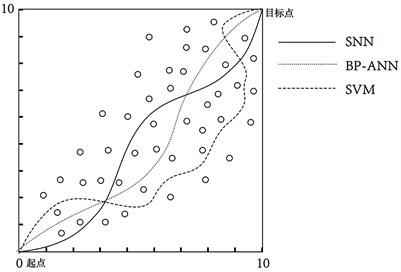
Figure 10. Vehicle trajectory under different network models when increasing the number of obstacles
图10. 增大障碍物数量不同模型下小车运行轨迹
4.2.2. 小车转向角结果分析
通过SNN、BP-ANN和SVM三种避障网络模型对小车在同一时间段内不同时刻下的转向角度进行预测,每组共记录6个值,如下图所示:
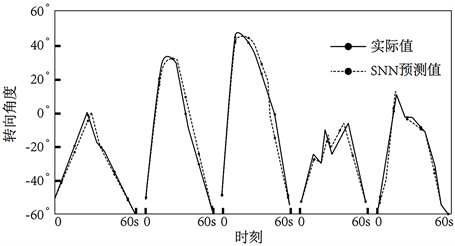
Figure 11. Results of SNN model schematic diagram
图11. SNN模型的转向角度结果示意图
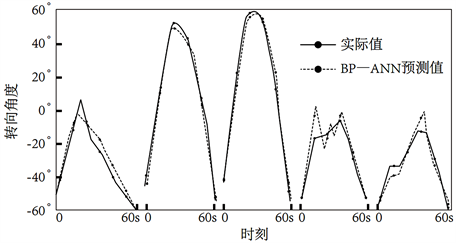
Figure 12. Results of BP-ANN model schematic diagram
图12. BP-ANN模型的转向角度结果示意图
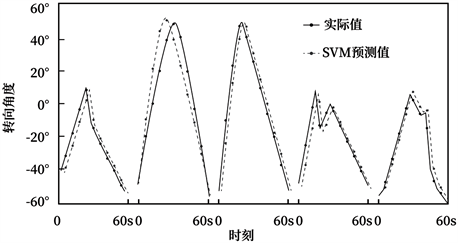
Figure 13. Results of SVM model schematic diagram l
图13. SVM模型的转向角度结果示意图
避障网络模型的预测结果从上图11~13中可以看出,这三种模型中SNN模型和BP-ANN模型的对比结果较为吻合,并且相对于BP-ANN模型来说,SNN模型的转向角预测结果曲线更贴合实际结果曲线,但通过SVM模型得到的值却与实际值相差较远,与实际曲线的重合率相对于其他两种模型更低。
4.2.3. 准确率
将本文算法模型分别与BP-ANN模型和SVM模型在测试集上的分类效果进行对比如表2所示。

Table 2. Accuracy of SNN, BP-ANN and SVM models
表2. SNN、BP-ANN和SVM模型的准确率
综上所述可以看出本文研究的SNN算法模型相对于BP-ANN模型和SVM模型,避障精度有所提高,避障结果稳定性也有了一定的改善,所以,SNN模型为最佳避障模型。
5. 结论
本文提出了一种基于脉冲神经网络的智能小车自动避障控制模型。脉冲神经网络作为“第三代神经网络”,不仅功耗低,计算能力强大,还附带时空信息和生物仿真性能等优点,使避障控制模型具有更好的学习能力。本文主要研究了基于无监督学习的脉冲神经网络的连接结构和学习算法,在现有的STDP规则的全连接网络中提出了稀疏概率连接网络结构,提高了脉冲神经网络的效率和性能。在建模过程中,根据测试样本数据中小车与障碍物的距离、角度以及小车的行驶速度等路况,采用灰色关联分析法确定了训练样本中的相似路况,使得模型对于不同的路况信息有更好的适用性。通过实验验证了SNN模型相对于SVM、模糊神经网络和BP-ANN模型有更好的有效性和适用性,因此,本文提出的基于SNN的小车的自动避障算法模型为智能车俩开发避障控制算法提供了一定的理论依据和应用价值。