1. 引言
随着网络越来越发达,各种信息更是无处不在,手机会收到广告信息,浏览器和播放器及各种网站上也会经常弹出垃圾信息。我们开始考虑研发了各种垃圾信息的识别系统去识别和阻拦一些对没用的信息。互联网的快速发展及电子邮件的应用也更加的方便快捷,垃圾邮件却不断地充斥我们的视野使得有意义的信息被覆盖,所以对垃圾信息的识别处理更受到重视。垃圾邮件的识别可以通过某些信息如:某种关键词出现次数、邮件的来源地址等。本文选取的是美国的一个邮件数据库,该数据中垃圾邮件的识别变量分成57个特征信息,通过区分垃圾邮件和非垃圾邮件57个变量不同取值情况来识别是否为垃圾邮件。对垃圾邮件的识别算法有很多,我们常见的就是建立回归模型来预测和识别垃圾邮件。
本文选择了偏最小二乘法建立回归模型,并与最小二乘主成分回归方法进行对比分析,李雪和孙建平(2017) [1] 对偏最小二乘回归进行了改进,并提出了基于正交投影修正的偏最小二乘回归算法,以此建立了烟气含氧量预测模型,并通过数据验证发现改进后的算法建模有较高预测精度且采样过程更快。本文采用LGK双对角化实质上也是运用了类似正交投影的思想,通过LGK双对角化将自变量与因变量的矩阵转化为正交矩阵的乘积的形式,然后进行主成分分析。L. Elden (2014) [2] 考虑多元线性回归,分析了计算投影到下维子空间的偏差最小二乘法,给出了PLS标准化理论分析。赵晓丹和徐燕(2014) [3] 详细介绍了垃圾邮件的概念及分类识别原理,并进行了垃圾邮件处理技术的对比分析研究,包括预处理、特征选择和分类三大步骤。其中特征选择技术包括文档频率、信息增益、优势率等方法。毛雪莲(2019) [4] 介绍了偏最小二乘法原理及算法的实现,偏最小二乘在数据的预处理中需要对数据进行标准化。陈龙等(2018) [5]、李雨亭(2018) [6]、黄鹤等(2018) [7] 基于机器学习方法对垃圾邮件进行了检测、识别。段同庆等(2019) [8]、丁学利和任鹏(2020) [9] 使用偏最小二乘法在其他领域进行运用;Keshav (2021) [10] 对偏最小二乘法进行了详细介绍;在垃圾邮件的分类研究中还存在其他方法下的算法研究 [11] [12] [13]。所以本文研究了基于偏最小二乘回归模型的垃圾邮件分类问题。
2. 研究问题
偏最小二乘(PLS)回归是一种面向高维数据的回归分类方法,在化学计量等领域应用尤其广泛。当自变量维数大于样本量且变量间相关性强时,PLS方法常优于主成分回归(PCR)。
设y: n × 1为因变量,X: n × p为自变量对应的设计矩阵。回归最小二乘问题是:
(1)
当p较大时,常采取的处理是将β的解限定在某一个低维子空间中。即对于
,给定一组近似正交基
,代入
,最小二乘问题变为:
(2)
因此,此时的核心问题是如何确定
,效果良好的
应使
的下限较小。
3. 研究方法
3.1. PCR
主成分分析在多元统计中是一种降维方法,通过消去自变量之间的多重共线性,同时又不损失太多的信息来达到降维目的。主成分分析是要找到自变量的线性组合
,要求Z方差和最大且不相关,而这个线性组合满足列正交的系数矩阵 被称为因子载荷矩阵,这些独立的变量被称为主成分,矩阵 被称为得分矩阵。
PCR主要使用了SVD分解,对于
,令
,即是我们要求的
,且
的
选取仅与自变量数据有关。将
带入回归模型得到
,对系数β的估计采用最小二乘方法,得:
,
。
3.2. PLS
偏最小二乘法运用LGK双对角化将自变量与因变量分解为两个正交阵和双对角阵的乘积,相较于PCR,PLS不仅考虑了自变量X的多重共线性,还考虑了自变量与因变量之间的多重共线性,对X与Y合成的矩阵进行降维,所以,可以达到比PCR更好的降维效果。
3.2.1. LGK双对角化的概念
偏最小二乘回归使用LGK双对角化将原始变量X,y合并为一个新的变量
,对Z进行LGK双对角化,表示为:
(3)
其中,
和
,分别为
与
的p个householder矩阵相乘构建的正交阵,矩阵
为:
(4)
令
为矩阵
删去第一行。
3.2.2. LGK双对角化的性质
记
为矩阵P的第i列,
为矩阵W的第i列,LGK双对角化性质如下:
· 令公式(3)左右同时左乘
,可以得到:
(5)
所以,有
,即
,
· 令公式(3)左右同时右乘W,可以得到:
(6)
所以,有
,即
(7)
· LGK的 矩阵第一列有
,且W矩阵具有如下形式:
 ,则
,
,
,则
,
,
LGK这三条性质为P、B、W矩阵的迭代算法提供了迭代初始值和迭代关系式。
4. 算法实现
4.1. P, W矩阵的迭代算法
由LGK的性质关系知,P、B、W三者之间的关系,其中,
,
,
为正交阵。首先,定义两个空的矩阵P、W,由第三条性质可知迭代初始值为:
将初始值填充空矩阵第一列,然后进行迭代运算得到第一次迭代结果为:
同理,将第一次迭代结果填充空矩阵的第二列,继续第二次迭代结果为:
…
最后,将以上每次迭代结果都相应的填充到P、W矩阵中,即可得到正交阵P、W。但是在计算
,
存在一定的误差使得我们得到的矩阵是近似列正交。则
就是
矩阵中选取前k列。
4.2. 邮件分类算法
本文选取spam.data数据集,其中包含4601封邮件(其中1813封为垃圾邮件),58个变量(其中第58个变量显示该邮件是否是垃圾邮件:是−1,否−0)首先,将该数据集分为训练集和测试集:
训练集:906封垃圾邮件,1394封非垃圾邮件
测试集:907封垃圾邮件,1394封非垃圾邮件
并对选取好的训练集和测试随机排序,在该问题中,
,
,
,
。
Step 1:将训练集数据代入迭代算法中,通过迭代最终得到
,此时回归模型为:
Step 2:将
看作新的变量,然后利用最小二乘法估计计算新的线性模型系数
,计算结果为:
,预测值为:
Step 3:利用测试集去代入预测模型,将得到的预测值与真实值比较,计算相应的分类准确率(真阳率、真阴率),图示不同k值对应的分类准确率以及ROC曲线图,分析该方法的整体识别分类效果。
5. 结果展示与分析
5.1. 不同k值下分类准确率分析
根据选取的k值的不同,即主成分个数的不同,所对应的分类准确率也不同。本文选择的指标为平均分类准确率、真阳率(垃圾邮件分类准确率)和假阳率(非垃圾邮件分类准确率)。不同的k值下的分类准确率为如表1所示:

Table 1. Classification accuracy under different k values
表1. 不同k值下的分类准确率
上表中括号中是利用PCR方法取相同k值时对应的分类准确率,用PLS计算得到的各种分类准确率都很高,当k = 5之后PLS方法对应的分类准确度已经稳定。同等情况下,PCR得到的分类准确度还未稳定,且值较低。所以下面给出了真阳率和真阴率随k值变化的趋势图如图1所示。
由图1可知,PLS方法得到的真阴率和真阳率在k = 5之后就稳定了,这与表1数据刚好对应,由于在之后准确率与k值的关系不大,可以选择更小的k值来进行建模和预测。
5.2. 不同分类截点下分类准确率分析
不同分类截点会使分类的结果不同,相应影响各种分类准确率的差别,所以本文选择分类截点cut在(−1.6, 2.2)之间,画出了对应的平均分类准确率cr、真阳率(垃圾邮件分类准确率) tpr和真阴率(非垃圾邮件分类准确率) tnr的变化趋势如图2所示:
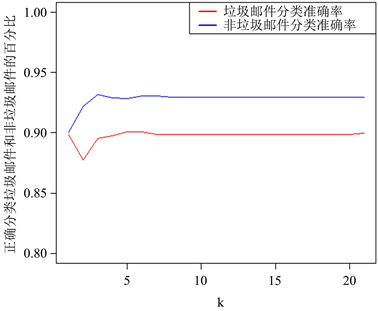
Figure 1. Accuracy rate change trend graph
图1. 准确率变化趋势图

Figure 2. Classification accuracy percentage line chart
图2. 分类准确率百分比折线图
在左图中,横坐标是分类截点的值,纵坐标表示了总的平均分类准确率,从左图中可以看出总的分类准确率随cut的增大而增大,当cut值取0附近时,分类准确率达到最高,之后又呈现一种下降趋势。右图中,横坐标也是分类截点,纵坐标为真阳率或真阴率值,图中红色线是真阳率,蓝色的是真阴率。cut的取值越大,真阴率越大即非垃圾邮件分类正确率越高,cut值越小,真阳率越大即垃圾邮件分类正确率越高。所以在具体操作中可以根据我们追求的目标而选择不同的分类截点。
5.3. 不同k值对应的ROC曲线图
受试者工作特征曲线(receiver operating characteristic curve,简称ROC曲线),又称为感受性曲线。受试者曲线就是以假阳率为横轴,真阳率为纵轴所组成的坐标图,和受试者在特定刺激下由于采用不同的判断标准得出的结果画出的曲线。在该问题下,ROC曲线具有如下作用:
· ROC曲线能容易地查出任意界限值时对垃圾邮件的识别能力。
· 选择最佳的诊断界限值。ROC曲线越靠近左上角,实验的准确性就越高,最靠近左上角的ROC曲线的点是错误最少的最好阈值,其假阳性和假阴性的总数最少。
· 两种及以上不同诊断试验对疾病识别能力的比较。越靠近左上角的曲线识别的准确度越高。
两种方法下取不同k值对应的ROC曲线如图3所示:
上图分别是PLS和PCR两种方法对应的ROC曲线图,两图的横坐标都是假阳率,纵坐标都是真阳率。在左图中,可以很明显看到随着k的变化,整个ROC曲线图很快达到了稳定状态,当k取5时真阳率的变化趋势几乎不再变化。而在右图中,从k = 1直到k = 30真阳率的变化趋势一直在变化,甚至到30 时还没有收敛,也即是k值的变化对真阳率的影响较大。除此之外,左边的ROC曲线整体比右边的靠近左上角,也即是PLS方法比PCR方法在对垃圾邮件的识别中更加有效,而且PLS在k值取很小时就已经达到了很高的识别准确度,所以在对垃圾邮件识别问题中PLS方法更加的有效。
6. 结论
偏最小二乘法的运用与最小二乘相比具有很大的优势。最小二乘是通过最小化误差的平方和来寻找数据的最佳函数匹配,利用最小二乘法可以简便地求得未知的数据,并使求得的数据与实际数据之间误差平方和最小。偏最小二乘法能够在自变量存在严重多重共线性的条件下进行回归建模;允许在样本点个数少于变量个数的条件下建模。本文中是基于偏最小二乘利用LGK双对角化设计了迭代算法和分类算法,对垃圾邮件分类问题进行了研究,并且分析了选取不同个数的主成分下分类准确度变化,还与PCR方法进行了比较,发现PLS的稳定性及识别垃圾邮件的准确性远远高于PCR。在最小二乘法主成分回归的迭代中,主成分个数需要选择将近30才能达到较好的效果,但是对于偏最小二乘法仅需5个主成分就可以达到比最小二乘更好的效果。所以,相比之下本文所用的基于偏最小二乘法的邮件分类算法更加的有效、准确度更高、速度更快。
致谢
感谢老师对本研究课题的指导,对于该研究的理论基础与编程问题比较困难,在这一过程中,老师与同学帮助了我很多,通过一步一步地推导与演练最终完成算法的实现。此外,也感谢论文评阅老师们的辛苦工作。