1. 引言
图论可以看作是对纽结理论的一种推广,它也是拓扑学领域中的重要组成部分,图的等价分类问题在图论中具有十分重要的地位与作用,而图的多项式作为图的不变量已经被国内外许多专家学者在各方面进行了深入的研究,这为图论奠定了坚实的基础。Yamada多项式作为图论中重要的多项式不变量,与chromatic多项式 [1] 之间有着紧密的联系。
本文主要研究一类特殊连图的Yamada多项式。在预备知识部分我们将介绍图论及图的Yamada多项式的一些基本概念;在第二部分我们将主要介绍图的Yamada多项式的性质;第三部分根据两点连图的性质,计算出了特殊连图(1, n)与图(m, n)的Yamada多项式,最后,通过研究计算得到了一类特殊的三点连图Yamada多项式的具体表达式。
2. 预备知识
2.1. 图的基本概念
定义2.1 [2] 图G是指一个有序三元组
,其中
是图G的顶点集,
是图G的边集且
,
是关联函数,它将G的每条边对应于G的无序顶点对(可以是相同顶点)。若边e和两个顶点u和v满足
,则称边e联结顶点u和v,顶点u和v称为边e的端点。
注释2.1 以后为了方便,分别用V和E表示图G的边集和顶点集。
注释2.2 如果有一条边连接相同的顶点,那么我们称这样的边为环(loop)。
2.2. 洛朗多项式的定义
定义2.2 [3] 图
,V是G的顶点集,E是G的边集。
和
分别表示图的连通分支数和一维Betti数。且
,
是一个2-洛朗多项式:
注释2.3 F是E的子集,
是F包含元素的数目,
且x和y是不定元,定义
。且
。
2.3. Yamada多项式的定义
定义2.3 [3] 将
和
代入到多项式
中,我们就得到一个多项式
:
称
为图G的Yamada多项式。
2.4. 两点连图的定义
定义2.4 [4] 若
为图G中的两个点,
为图H中的两个点,将
和
粘合成一个新的顶点u,再将
和
粘合成一个新的顶点v,得到一个新图
,称图
为G和H的两点连图。
3. Yamada多项式的性质
为收缩边e得到的图,
为删除边e得到的图。
给定两个图
和
,
表示图
和
的不交并,
表示图
和
的一点并。我们称G有一割边e,如果
比G有更多的连通分支数。
性质3.1 [1]
。
证明:由于
,
因此
。
性质3.2 [1] 如果图G有一条割边,则
。
证明:设e是G的割边,则
,
,由
的性质得,
因此
。
性质3.3 [1]
,e是环边。
证明:记
,
,那么
,
,
,则
因此
。
性质3.4 [1]
,e是非环边。
证明:记
,
,那么
,则
因此
。
性质3.5 [1]
。
证明:记
,
,且
,
,那么
,
,则
因此
。
性质3.6 [1]
。
证明:记
,
,且
,
,那么
,
,则
因此
。
4. 一类连图的Yamada多项式的性质
4.1. 两点连图Yamada多项式的性质
定理4.1 [1] 图
和
有两个公共顶点u和v,
表示图
和
的两点并,
和
分别是粘接图
和
的顶点u和v得到的图,则
4.2. 图
的Yamada多项式的性质
定义4.1 [5] 给定两个图G,K,
,
是图G的任意两个顶点,
,
是图K的任意两个顶点,将顶点
,
用一条边连接起来,
,
用n条边连接起来,如图1所示,所得到的图记作
,
。
定理4.2 对于图
,
,有
其中:
,
分别为图G,K的Yamada多项式;
为图G,K的两点并的Yamada多项式,
。
证明:利用性质3.4,对图
的n条边中的一条边进行缩边减边的运算,再对
条边进行缩边减边的运算,以此类推,那么有等式
成立,其中
,则
(1)
由(1)式可知,
所以
(2)
另外
,将其代入到(2)中,得
其中图
,F如图2所示。
4.3. 图
的Yamada多项式的性质
定义4.2 [5] 给定两个图G,K,
,
是图G的任意两个顶点,
,
是图K的任意两个顶点,若顶点
,
用m条边连接起来,
,
用n条边连接起来,如图3所示,所得到的图记作
,且
。
图2.
,F
定理4.3 对于图
,
,有
其中:
,
分别为图G,K的Yamada多项式;
为图G,K的两点并的Yamada多项式,
。
证明:首先利用性质3.4,对图
的m条边其中的一条边进行缩边减边运算,得到图
,再对图
的n条边进行运算,其次对
条边进行缩边减边运算,以此类推,那么有等式
成立,其中
,则
且
,代入上式中得
(3)
另外有
综上所述我们得到
将其代入(3)式可得
由此我们可以得到
其中图
,
,
如图4所示。

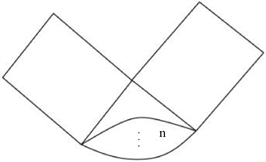
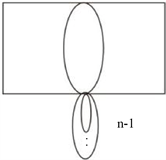
Figure 4.
,
,
图4.
,
,
4.4. 一类三点连图Yamada多项式的性质
定理4.4 给定两个图
和
,
表示图
和
的三点连图,其中顶点
,
,设图
中的顶点u与w,v与w之间无边且无环边,图
中的顶点
与
,
与
之间无边且无环边。
及
分别为粘接图
和
的顶点u与v,u与w,v与w,
及
与
,
与
,
与
,
得到的图,则
(4)
证明:令
,
,
分别表示图G的顶点个数与边的个数,下面通过对图G的边数
用归纳法来证明这一定理。
若
,那么
和
都是由孤立顶点组成。假设
,
,则G是由
个孤立点组成的图。由性质3.1和性质3.5,得
。
又因为
,
,
,
,
,
,
,
,将其带入等式(4)的右边有:
因此等式(4)成立。
现在假设当
时,定理4.4成立,其中
。那么我们不妨设
,图
,e为图G的一条边,我们不妨假设
。我们分两种情况进行讨论:
情况1. e是不连接顶点
的边,那么e为
的一条非环边。因此,
且
因此,
情况2. e是连接顶点
的边,那么e为
的一条环边。由性质3.3及定理4.1得
且
因此,
定理4.4得证。
5. 结语
本文主要研究了一类特殊空间图的Yamada多项式的性质,通过利用Yamada多项式的性质,在两点连图的基础上,构造出了一类特殊的连图并给出了其具体表达式。未来还可以对空间图Yamada多项式的性质做进一步的研究。