机载防撞系统ACAS X高度跟踪器目标跟踪算法

Target Tracking Algorithm of Airborne Collision Avoidance System ACAS X Height Tracker

摘要: 高度跟踪器能否有效地在新一代机载防撞系统(ACAS X)的垂直面上工作是设计的关键。在传统研究中，高度率估算不够准确是非线性跟踪器的一个弊端，线性跟踪器因报告中的“粗量化”精度使得性能劣化。为了使目标飞机状态值处理更加稳定，该研究使用量化量测状态估计算法，将飞机状态不确定性作为概率分布来描述，量化视为高斯噪声并使用Sheppard校正，通过Kalman滤波算法对飞机垂直面上的状态进行估计。实验结果显示，该算法在高度跟踪的精度上优于传统设计，可以有效做出防撞决策，为ACAS X系统提供更高的可靠性。

Abstract: Whether the height tracker can effectively work on the vertical plane of the new generation of air-borne collision avoidance system (ACAS X) is the key to the design. In traditional research, inaccurate height rate estimation is a drawback of nonlinear trackers, and linear trackers have deteriorated accuracy due to the “coarse quantization” reported in the report. In order for the tracker to process the target aircraft state more stably, the research uses quantitative measurement state estimation algorithm, which describes the aircraft state uncertainty as a probability distribution, quantizes it as Gaussian noise and uses Sheppard correction, and estimates the state of the aircraft on the vertical plane through the Kalman filter algorithm. Experimental results show that the algorithm is superior to traditional designs in high tracking accuracy, can effectively make anti-collision decisions, and provide higher reliability for ACAS X.

1. 引言

二十世纪八十年代，林肯实验室使用基于α-β滤波原理的高度跟踪器 [1]，为机载防撞系统(Traffic Collision Avoidance System, TCAS)的设计提供高度和高度率的有效估计，但是α-β跟踪器对飞机高度报告不进行飞机真实意图判断就进行平滑处理，会产生瞬态过冲现象，不利于防撞决策的选择 [2]。目前，全球范围的民航飞机装备的TCAS II都是采用非线性高度跟踪器，它利用高度量化层占用时间间接估计高度率的方法，解决了α-β跟踪器带来的性能劣化。在传统高度跟踪器的滤波算法中，无论是α-β线性 滤波，还是非线性滤波器，例如无迹卡尔曼滤波、扩展卡尔曼滤波等，在处理高度数据时，将数据点作为独立的测量值，导致误差的不相关性，可能产生与实际情况相悖的结果 [3]。

针对以上问题，本文参考RTCA (Radio Technical Commission for Aeronautics)制定的《机载防撞系统X (ACAS X)的最低运行性能标准》，使用一种量化量测进一步划分为小区间求均值近似的最小均方误差估计(MMSE)的方法，对目标飞机的高度观测值进行估计，即将状态的不确定性作为概率分布，量化过程视为高斯噪声并使用Sheppard校正处理量化，通过卡尔曼滤波预测值，修正目标飞机的高度观测值，完成了对目标飞机在垂直方向上的高度跟踪器跟踪算法的设计与仿真 [4]。

2. α-β跟踪器滤波原理

在传统的机载防撞系统中，当气压高度以25 ft量化精度生成高度报告时，高度跟踪器采用的滤波方式是α-β滤波器，这种滤波方式的原理和实现较为简单 [5]。

α-β滤波器是针对匀速运动目标的一种常增益滤波器，其形式和Kalman滤波器相似。经过一步预测得到的预测值，其值与测量值之间存在的残差，记为 ${\hat{r}}_k$。当目标飞机数据传入高度跟踪器时，采用选定的α和β常数，使用残差的α倍校正飞机的高度估计，使用β乘以残差来校正飞机的高度率估计：

${\hat{z}}_k={\hat{z}}_{k|k-1}+\alpha {\hat{r}}_k$ (1)

${\widehat{\stackrel{\dot{}}{z}}}_k={\widehat{\stackrel{\dot{}}{z}}}_{k|k-1}+\left(\beta /T\right){\hat{r}}_k$ (2)

式中， ${\hat{z}}_k$ 是高度估计值， ${\hat{z}}_{k|k-1}$ 是高度的一步预测值， ${\widehat{\stackrel{\dot{}}{z}}}_k$ 是高度率估计值， ${\widehat{\stackrel{\dot{}}{z}}}_{k|k-1}$ 是高度率的一步预测值。为了保证系统的稳定性，α和β是一个很小的正值，满足： $0<\alpha <1$， $0<\beta \le 2$， $0<4-2\alpha -\beta$。

3. 非线性高度跟踪器滤波原理

对于S模式25 ft和C模式100 ft量化精度的高度报告，会因为“粗量化”精度的存在导致线性跟踪器性能的劣化。为了有效改善高度跟踪器性能，TCAS II使用了非线性跟踪器 [6]。其原理将同一高度量化层内的所有数据点都作为高度变化率的单次观测，而对高度率的估计通过对高度量化层占用时间的平滑滤波来完成。

假设当前高度为 $Nq+{\epsilon }_{0}q$，其中N为整数且 $0\le {\epsilon }_0<1$， ${\epsilon }_0$ 是飞机初始高度在量化精度为q = 100 ft的高度量化层的真实位置，则飞机高度为

$z\left(t\right)=Nq+{\epsilon }_{0}q+\stackrel{\dot{}}{z}t$ (3)

假设在同一时间间隔内高度变化率恒定，飞机在一个高度量化层占用时间为

$T=\frac{q}{\left|\stackrel{\dot{}}{z}\right|}$ (4)

则飞机高度变化率估计值为

$\widehat{\stackrel{\dot{}}{z}}=d_t\frac{q}{\hat{T}}$ (5)

式(5)中， $d_t$ 表示最近的高度量化层跃变的符号(+1表示高度增加，−1表示高度降低)。飞机高度穿越连续两个高度量化层的时间差则作为高度量化层占用时间的测量值 $T^{\prime }$， $T^{\prime }$ 的测量误差由采样率决定，通过对连续的测量值T的平滑滤波得到当前高度量化层占用时间的估计值 $\hat{T}$，最终得到当前高度率的估计值 $\widehat{\stackrel{\dot{}}{z}}$。

4. ACAS X高度跟踪器

TCAS系统的跟踪器旨在产生垂直速率的单点估计，而ACAS X是在TCAS II的基础上升级的新一代机载防撞系统，将飞机状态的步确定性考虑在内，这样可以改善TCAS设计的局限性，优化成本函数和决策逻辑，大大提高防撞性能和降低报警率 [7]。ACAS X的跟踪器沿用了TCAS跟踪器的设计思路，将复杂的三维空间目标跟踪问题分解为水平和垂直两个维度，分别设计了水平跟踪器和垂直跟踪器。垂直跟踪器也称为高度跟踪器，用于对目标飞机的高度和高度率进行状态估计。

在机载防撞系统ACAS X中，主动监视模块通过C/S应答器获得关于目标飞机的高度、高度率等信息，打包发送到高度跟踪器，对接收到的信息进行滤波、预测 [8]，最后形成关于目标飞机的垂直方向状态的准确估计，为下一步防撞决策提供可靠信息 [9] [10]。

4.1. 高度跟踪器算法流程

机载防撞系统将接收到的目标飞机信息，结合本机的位置、速度等信息进行数据关联、滤波、预测、更新等处理，实现高精度快速估计飞机的飞行航迹，为后续防撞决策提供可靠数据。对目标飞机垂直状态的跟踪，本文将实时性良好的标准Kalman滤波算法与近似最小均方误差估计(MMSE)相结合 [11]，应用于高度跟踪器中，称为量化量测Kalman滤波方法。机载防撞系统ACAS X高度跟踪器的数据处理流程如图1所示，其具体实现步骤如下：

Step 1：建立目标飞机的运动模型，得到目标飞机的状态方程和量测方程；

Step 2：对目标飞机的初始状态和误差的协方差进行初始化；

Step 3：使用k − 1时刻的估计值，对k时刻目标的状态进行一步预测，并计算一步预测误差的协方差；

Step 4：由给出的系统模型中的变量及一步预测误差协方差，计算Kalman增益；

Step 5：引入观测值、预测值以及量化区间，使用MMSE状态估计算法；

Step 6：更新k时刻目标的状态估计，并且更新k时刻状态误差的协方差。

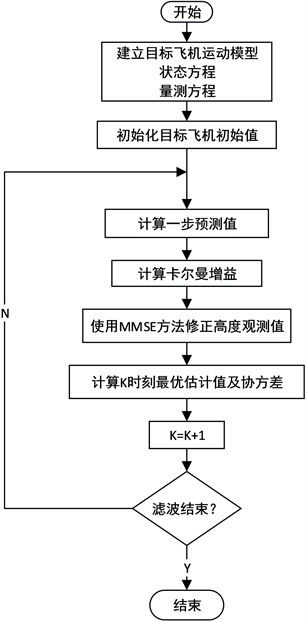
Figure 1. ACAS X height tracker data processing flow

图1. ACAS X高度跟踪器数据处理流程

步骤五在标准Kalman滤波算法的基础上，增加了处理高度报告的量测量化部分，可以使误差高度相关联，再用Kalman滤波预测值修正目标飞机的高度观测值。相比于TCAS II中非线性滤波算法通过平滑占用时间估计高度率的方式，本文给出的高度跟踪算法具有较好的准确性和可靠性。

4.2. 高度的量化量测Kalman状态估计

量化量测下目标跟踪最主要的目的是处理不精确类型的量测信息，本文使用了量化量测中的近似最小均方误差估计(MMSE)方法，其思路就是通过分段估计的方法，采用离散累计概率分布函数来近似连续概率密度函数的积分问题。

假设目标的先验概率为高斯分布，利用高斯分布概率公式，即 $f\left(x\right)=\frac{1}{\sqrt{2\pi \delta }}{\text{e}}^{-\frac{{\left(x-\mu \right)}^2}{2{\delta }^2}}$ 计算各分区中间点的概率密度，用d表示概率分布的分。

$d={\displaystyle \underset{i=1}{\overset{L}{\sum }}{\text{e}}^{-\frac{{\left(g\left(i\right)-\mu \right)}^2}{2{\sigma }^2}}}$ (6)

式中 $\mu$ 为高度观测值的均值，取值为量测的一步预测值 ${\hat{z}}_{k|k-1}$ ； ${\sigma }^2$ 为高度观测值的方差。

高度和高度率的近似最小均方误差估计(MMSE)步骤如下：

Step 1：对高度的观测值z进行处理。将k时刻获得的高度观测值z进行分割，量化量测值z对应的取值区间为： $\left[z-\frac{q}{2},z+\frac{q}{2}\right]$，把量化量测值进行分割就是将区间分为L个高度分区，可求得每个分区的中点值为：

$g\left(i\right)=z+\frac{1}{L}\left[\left(2i-1\right)-L\right]\frac{q}{2}$ (7)

式中L = 20，q是量化步长，对于C模式应答机q的取值为100 ft，对于气压高度计q的取值为25 ft。

Step 2：假设目标飞机的高度观测值落在每个分区的概率符合高斯分布，利用高斯分布的概率公式，求出落在每个分区中间点g(i)的概率密度.在计算高斯分布的概率密度时，采用量测的一步预测值及其预测误差的协方差，作为高度观测值的均值和方差。

$p\left(i\right)=\frac{1}{d}{\text{e}}^{-\frac{{\left(g\left(i\right)-\mu \right)}^2}{2{\sigma }^2}}$ (8)

Step 3：利用最小均方误差公式，以及离散型随机变量的均值和方差公式，计算每个分区的中心点g(i)偏离高度估计值 $\hat{z}$ 的均值和方差，从而得到高度观测值的均值以及高度观测误差的方差。

高度观测值的均值：

${z^{\prime }}_k={\displaystyle \underset{i=1}{\overset{L}{\sum }}p\left(i\right)\left[g\left(i\right)-{\hat{z}}_{k|k-1}\right]}$ (9)

高度观测误差的方差：

${R^{\prime }}_k=E\left[{\left(g\left(i\right)-{\hat{z}}_{k|k-1}\right)}^2\right]-{\left(E\left[g\left(i\right)-{\hat{z}}_{k|k-1}\right]\right)}^2$ (10)

式中 ${z^{\prime }}_k$ 是预测的k时刻的高度量测值， ${R^{\prime }}_k$ 是预测的k时刻高度量测误差的协方差。

5. 仿真结果分析

为了验证机载防撞系统ACAS X高度跟踪算法的效果，本文根据RTCA DO-385标准，飞机飞行在垂直方向上可分为：平稳飞行、匀加速飞行和匀速飞行三种飞行状态，据此设计了匀速飞行过程中使用α-β滤波、Kalman滤波和量化量测Kalman滤波，三种滤波方法进行仿真验证。

为了验证高度跟踪算法的正确性和有效性，选取匀速运动模型，仿真周期T为1 s：

状态方程：

$x_k=F{x}_{k-1}+G{w}_{k-1}$ (11)

量测方程：

$z_k=H{x}_k+v_k$ (12)

式中状态 $x_k$ 包含飞机的高度和高度率， $z_k$ 为观测值， $w_k$ 为状态噪声， $v_k$ 为量测噪声，都是零均值白噪声，参考ACAS X性能标准，方差分别是 $Q=5{\text{ft}}^{\text{2}}/{\text{s}}^{\text{4}}$ 和 $R=22.09{\text{ft}}^2$。状态转移矩阵 $F=\left[\begin{array}{cc}1& T\\ 0& 1\end{array}\right]$，观测矩阵 $H=\left[\begin{array}{cc}1& 0\end{array}\right]$，过程噪声耦合矩阵 $G=\left[\begin{array}{c}\frac{1}{2}{T}^2\\ T\end{array}\right]$，量化步长q可取100 ft和25 ft。

1) 当高度报告为25 ft时，三种滤波效果误差近似。为了仿真效果更明显，按民航飞机飞行，设定飞机初始化高度为180 m开始匀速上升飞行，高度率为200 m/s，量化步长q = 100 ft，按照4.1小节高度跟踪器的处理流程，得到经量化量测Kalman滤波处理后的高度轨迹如图2所示。

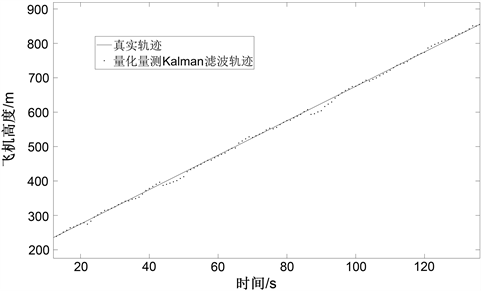
Figure 2. Quantitative measurement of Kalman filter simulation effect diagram

图2. 量化量测Kalman滤波仿真效果图

2) C模式下目标飞机的跟踪性能较差，且估计的高度滤波存在振荡行为，尤其在标准Kalman滤波中该行为影响较大。针对这一问题，为了验证本文4.1小节所述方法的有效性，使用同一条件仿真，并将结果与标准Kalman滤波的结果对比。图3为量化量测Kalman滤波与标准Kalman滤波对高度估计误差的对比。

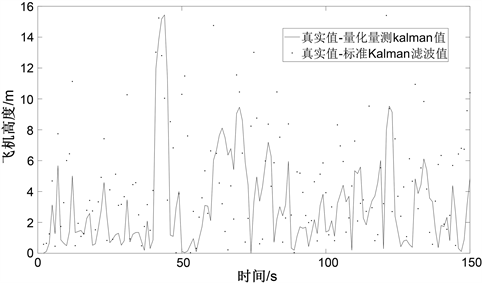
Figure 3. Quantized measurement Kalman filter and the standard Kalman filter error comparison diagram

图3. 量化量测Kalman滤波与标准Kalman滤波误差对比图

3) TCAS系统中α、β在仿真中分别设定值为0.27和0.4，此值满足系统稳定性要求，且是在相同条件下滤波效果最好的取值。为了验证本文4.1小节所述方法的有效性，使用同一条件仿真，并将结果与TCAS系统中α-β滤波器的结果对比。图4为量化量测Kalman滤波与α-β滤波对高度估计的误差的对比。

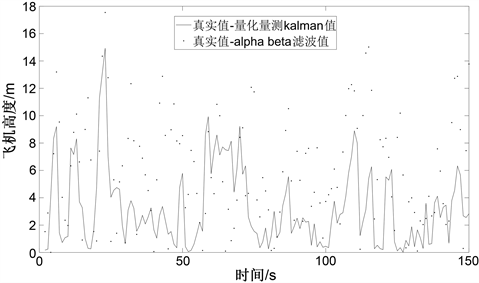
Figure 4. Quantified measurement of Kalman filter and α-β filter error comparison diagram

图4. 量化量测Kalman滤波与α-β滤波误差对比图

6. 结束语

机载防撞系统ACAS X高度跟踪器是建立在标准Kalman滤波算法的框架上，提出了一种近似最小均方误差(MMSE)状态估计算法。该算法保留了Kalman滤波良好的滤波性能，进行更新状态值(飞机高度/高度率)之前，先对飞机的高度观测值进行量化量测分区，利用高斯分布的概率公式计算高度观测值落在每个分区的概率，再使用MMSE状态估计算法计算每个分区对中心点的偏离度，修正其观测值及方差。计算机仿真结果显示，在仿真条件相同的情况下，该方法对比于TCAS系统中的α-β跟踪算法和标准Kalman滤波算法，对目标飞机的高度估计更加接近真实值，特别是在C模式100 ft高度报告的情况下效果更明显，减小滤波误差，有效地减小高度量化对飞机跟踪的不确定性，也解决了高度报告“粗量化”的特性，可以为飞机防撞决策提供可靠的高度状态信息。本文仿真环境的设定均根据RTCA DO-385标准，并未采用真实的飞行高度报告信息进行模拟，下一步的工作将在获得真实高度报告后进行验证。

基金项目

西南民族大学2021年研究生“创新性科研项目”(项目编号CX2021SP109)。

NOTES

^*通讯作者。