基于层次分析法对项目财务投资决策指标的评价

Evaluation of Project Financial Investment Decision Index Based on AHP

摘要: 项目财务投资是从管理会计的角度，通过评估和总结企业经营状况与投资决策指标，以特定项目为研究对象的一种长期决策行为。与其他相关分析比较，指标选取更注重影响时间、变现能力和风险的考量，需要为企业在日趋激烈的市场环境中制定科学合理的规划提供直观数据。基于此，本文利用AHP模型构建了综合投资决策评价体系，并对净现值和内含报酬率进行适时修正，避免在互斥项目中出现结果分歧。最终帮助公司极大程度地兼顾投资项目决策的收益性和稳健性。

Abstract: Project financial investment is a kind of long-term decision-making behavior from the perspective of management accounting, which takes a specific project as the research object by evaluating and summarizing the enterprise’s operating conditions and investment decision indicators. Compared with other related analysis, index selection pays more attention to the impact time, liquidity and risk considerations, which need to provide intuitive data for enterprises to make scientific and reasonable planning in the increasingly fierce market environment. Based on this, this paper uses the AHP model to construct the comprehensive investment decision evaluation system, and timely revises the net present value and embedded rate of return, so as to avoid the divergence of results in mutually exclusive projects. Finally, it helps companies to take into account the profitability and robustness of investment project decisions to a great extent.

1. 引言

投资是企业为了在未来可预见的时期内获得收益或资金增值，在一定时期内向目标领域投放足够数额的资金或实物的货币等价物的经济行为 [1]。主要可划分为两方面，一方面是公司以货币投入特定项目，通过系列经营活动获得利润，亦可称为项目投资；另一方面是企业的资本金融投资，包括购买国债、股票等有价证券。本文主要探讨的项目投资，它对于企业生存与发展起到了举足轻重的作用。不仅是维护企业生产运作的基石，更是扩大再生产的推进器，不断增强企业的市场竞争力。在进行项目投资分析时，财务性指标相较于技术性指标和环境指标更为重要。因为只有在预测的现金流量基本准确的情况下，才能够得出完整且定量化的损益结果，帮助管理层做出适宜的决策，避免出现类似于海南航空破产重组的短视行为。

投资决策中对投资项目进行评价时所用的指标通常分两类：一类是静态投资指标，衡量和比较项目可行性时没有考虑时间价值因素，主要包括投资回收期和投资报酬率；另一类为动态投资指标，是考虑了时间价值因素的对象，具体包括净现值(NPV)、获利指数(PI)、内部报酬率(IRR)等。根据杜克大学教授J.R. Graham于2001调查数据显示，全美325家企业中仅有43.3%的企业选择了两种及以上的投资指标进行综合分析 [2]。随着市场不确定性增加，单一指标必然会导致决策片面化，若仅以投资回收期来考虑项目，就无法确切衡量方案在整个计算期内的经济效果。

综上所述，本文将从财务投资指标入手，通过问卷调查法收集分别来自高校和企业的四位专家意见，并结合层次分析模型建构全新的项目投资决策评价指标体系。

2. 文献综述

关于长期投资要素的研究最早是由J.L. Riggs于20世纪80年代提出，他在著作《工程经济学》中论证并系统阐释了资金时间价值、货币管理风险和不确定分析等，初步构建了项目决策财务体系 [3]。但他并没有对投资决策指标进行说明，H.G. Thuesen等学者基于时间价值原理认为，需根据项目的净现值(NPV)比较及优选方案，即净现值越大，表明该项目的报酬率越大，方案可取 [4]。然而，净现金流量的测算和折现率较难估计，无疑是给NPV指标的确定增加难度。与此同时，日本学者千住镇雄、伏见多美雄将内部报酬率(IRR)、投资回收期等引入到长期项目可行性研究中，极大程度地丰富了投资决策财务指标体系 [5]。

不难发现，国外对投资项目经济评价指标的研究起步较早，相关理论也较为完善。但在实证分析领域略有空缺，国内的专家学者刚好填补了应用深海。学者曾蔚、郭福全、陈红卫在公路建设方案选择中将净现值指标与盈利能力、贷款偿还能力相连结，从财务效益角度论证了项目投资的经济可行性 [6]。由于文章侧重于定量方法描述，没有对指标体系选取给出详细解释。学者党立军基于动态折现指标——净现值和内含报酬率进行案例分析，分别提出了在独立性投资项目决策和互斥性投资项目决策的应用方法，为本文指标修正提供了思路 [7]。同时，邵希娟、罗钰通过企业实例来阐述四种静态回收期指标的本质区别,说明各自的内含假设以及适用情形，从而总结出使用不同回收期指标进行项目投资决策的步骤 [8]。还有不少学者在房地产投资、配电网建设、先进制造设备等领域做出尝试，他们共同推动了项目投资决策财务指标的综合实践的发展 [9] [10] [11]。

综合现有文献来看，国内外学者在研究项目经济性时，侧重于使用单一投资指标，并且论证过程缺乏相应的数理模型。因此，本文基于层次分析法对修正后的投资决策指标进行综合评价。

3. 层次分析法

3.1. 层次分析法相关概念

层次分析法是美国匹茨堡大学教授T.L. Satty于20世纪70年代初，应用网络系统理论和多目标综合评价方法，提出的一种定量与定性研究相结合的系统决策方法。它把复杂问题转化为不同层次的元素聚集组合，通过因素间相互关联影响以及隶属度形成一个多层次的分析结构模型。从而使问题归结为最低层相对于顶层的相对重要权值的确定。具体计算流程如图1所示。

Figure 1. Calculation process

图1. 计算流程

3.2. 层次分析法计算步骤

3.2.1. 建立多级梯阶结构模型

首先，在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，通过梯阶层次的评价模型所表示(见表1)。其中，同一层的诸元素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。一般认为，A层为目标层，B层为准则层，C层为指标层。

Table 1. Evaluation index system

表1. 评价指标体系

3.2.2. 构造判断矩阵

基于多级梯阶模型，采用德尔菲法邀请专家对评价指标进行主观评价和综合分析。对同一层级中不同元素进行两两比对之后，按9分位比率(比较矩阵，表2所示)排定各评价因子的相对优劣顺序，依次构造出指标体系的判断矩阵 $S=\left\{a_{ij}\right\}$，其中应满足 $a_{ij}>0$。在得出m个专家评价意见后，通过公式(1)得出综合等级判断矩阵。

$S=\left(S_1+S_2+\cdots +S_n\right)/m$ (1)

Table 2. Scale of relative importance

表2. 相对重要性的比例标度

3.2.3. 计算不同层次下元素相对权重

针对某一个标准，计算各备选元素的权重；关于判断矩阵权重计算的方法有两种，即几何平均法和规范列平均法。本文选取规范平均法进行详细介绍。由于判断矩阵S中的每一列都近似地反映了权值的分配情境，故采用全部列向量的算术平均值来估计权向量，即：

$W_i=\frac{1}{n}{\displaystyle {\sum }_{j=1}^n\frac{a_{ij}}{{\displaystyle {\sum }_{k=1}^n{a}_{kj}}}}$， $i=1,2,3,\cdots ,n$

具体计算步骤为：

1) 计算判断矩阵每一列之和 $X_k$ ；

$X_k={\displaystyle {\sum }_{k=1}^n{a}_{kj}}$， $k=1,2,3,\cdots ,n$

2) 按列归一化处理，将判断矩阵每一列 $a_{ij}$ 除以 $X_i$，即得到： $a_{ij}/{\displaystyle {\sum }_{k=1}^n{a}_{kj}}$ ；

3) 将归一化后的新判断矩阵各列相加，记为 $Y_n$ ；

$Y_j={\displaystyle {\sum }_{j=1}^n{a}_{kj}}$， $j=1,2,3,\cdots ,n$

4) 相加后的向量通过公式得到每一个比较因子的权重 $W$

$W=\frac{Y_i}{{\displaystyle {\sum }_i^n{Y}_i}}$， $i=1,2,3,\cdots ,n$

3.2.4. 一致性检验及层次排序

虽然在构造判断矩阵 $S=\left\{a_{ij}\right\}$ 时并不要求结果具有一致性，但判断偏离程度过大会影响到最终决策结果。因此需要对判断矩阵S进行一致性检验。

1) 算一致性指标CI (Consistency Index)

$\text{CI}=\frac{{\lambda }_{\max }-n}{n-1}$，其中 ${\lambda }_{\max }$ 表示判断矩阵的最大特征值， $n-1$ 指自由度。

2) 对照同阶矩阵平均一致性表查找指标RI (见表3)

Table 3. Average consistency checklist

表3. 平均一致性检查表

3) 计算一致性比率CR (Consistency Ratio)

当CR < 0.1时，认为判断矩阵的一致性可以接受，否则将对矩阵进行适时修正。通过有目的地分配和调整各指标权重，可以表现出评价者在把握评价指标体系上的倾向性和灵活性。

最后，通过各指标对目标层的权重排序，进行分析解释或方案选择。特别注意对层次总排序也需作一致性检验。

4. 项目财务投资决策的层次分析模型

4.1. 基本思路

2020年是我国“十三五”规划的收官之年，突如其来的新型冠状病毒肺炎破坏了市场的乐观情绪，给中国乃至全球产业发展带来沉重打击。虽然中国现已逐步恢复，经济发展态势稳健增加，但企业营商环境仍充满不确定性，加之传统投资模式正在发生趋势性失效，这对评价项目投资提出了更高要求。前文已述，分析投资决策的关键是权重指标确定。相较于传统的德尔菲法，层次分析法更具客观性，利用判断结构(主要是两两比较)把专家意见和定量描述直接而有效地结合起来，从而保证评价结果的准确度。

4.2. 指标选取与修正

指标体系的构建是对项目财务投资决策进行综合评价的关键环节。为了避免出现指标选取缺乏全面性、系统性等问题，本文利用经验分析法选取了五项公司常用投资决策指标(图2)。

4.2.1. 投资回收期

投资回收期指自投资方案实施至收回初始投入资本所需时间，即能够使与此方案相关的累计现金流入量等于累计现金流出量的时间，公式表达为：

${\displaystyle \underset{t=1}{\overset{n}{\sum }}{I}_t}={\displaystyle \underset{t=1}{\overset{n}{\sum }}{Q}_t}$

式中， $I_t$ 为在项目实施第t年的净现金流入值； $Q_t$ 为在项目实施第t年的净现金流出值。投资回收期一般以年为单位。

4.2.2. 投资报酬率

投资报酬率也称为投资利润率，它表示年平均利润占总投资的百分比。投资报酬率愈高，项目可投资性越强。即

$投资报酬率=年平均利润/投资总额$

4.2.3. 净现值(NPV)

净现值指的是在方案的整个实施运行过程中，所有现金净流入年份的现值之和与所有现金净流出年份的现值之和的差额，如下：

$NPV=\underset{t=1}{\overset{n}{{\displaystyle \sum }}}\frac{I_t}{{\left(1+i\right)}^t}-\underset{t=1}{\overset{n}{{\displaystyle \sum }}}\frac{Q_t}{{\left(1+i\right)}^t}$

式中，n为项目实时运行的时间(年份)；i为预定的贴现率，一般选择资本成本率； $I_t$ 和 $Q_t$ 的概念同前。

若净现值大于或等于零，表明该项目的报酬率大于或等于资本成本率，方案可取；反之，则方案不可取。

4.2.4. 获利指数(PI)

获利指数也叫现值指数，是指在整个方案的实施运行过程中，所有现金净流入年份的现值之和与所有现金净流出年份的现值之和的比值，即

$PI=\frac{{\displaystyle {\sum }_{t=1}^n\frac{I_t}{{\left(1+i\right)}^t}}}{{\displaystyle {\sum }_{t=1}^n\frac{Q_t}{{\left(1+i\right)}^t}}}$

式中n，i， $I_t$， $Q_t$ 的含义与净现值公式相同。

若获利指数大于1，则表明该项目有一定的盈利能力，方案可取；反之，则方案不可取。

4.2.5. 内部报酬率(IRR)

内部报酬率反映的是方案本身实际达到的报酬率，它是在整个方案的实时运行过程中，当所有现金净流入年份的现值之和与所有现金净流出年份的现值之和相等时项目的报酬率，即能够使项目的净现值为零时的报酬率。满足方程 $Y_1$ 如下：

$\underset{t=1}{\overset{n}{{\displaystyle \sum }}}\frac{I_t}{{\left(1+i\right)}^t}=\underset{t=1}{\overset{n}{{\displaystyle \sum }}}\frac{Q_t}{{\left(1+i\right)}^t}$

同样，内含报酬率亦可以表示为方程 $Y_2$ 的形式：

$\underset{t=1}{\overset{n}{{\displaystyle \sum }}}\frac{NC{F}_t}{{\left(1+IRR\right)}^t}=0$

其中， $NC{F}_t$ 为项目第t年的净现金流量； $NC{F}_0$ 时项目初始投资额度。

在构建判断矩阵前，考虑到对初始投资不同的互斥方案进行决策分析时，使用净现值和内部报酬率可能会出现相反的选择。两种方法出现矛盾的根源是对期间资金再投资有不同的假设。基于此，笔者借鉴了学者张信东、刘维奇的方法对内含报酬率进行修正 [11]，将方程 $Y_2$ 两边同时乘以 ${\left(1+IRR\right)}^n$ 来计算终值。篇幅有限，修正过程不做详细说明，更新后的结果如下：

$NPV=\left(-NC{F}_0\right)\left[{\left(\frac{1+IR{R}^{\ast }}{1+r}\right)}^n-1\right]$

修正后的内部报酬率记作 $IR{R}^{\ast }$。可知，面向互斥方案的选择运用净现值法和修正内含报酬率法所作出的决策结果是一致的。

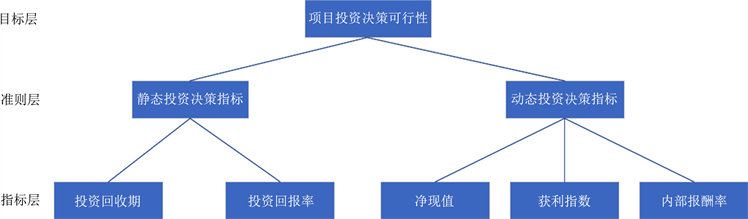
Figure 2. Evaluation index system of project investment decision

图2. 项目投资决策评价指标体系

4.3. 模型求解与分析

4.3.1. 模型求解

通过邀请八位专家(均为陕西某高校财务管理专业副高以上职称教师)对准则层各项指标进行两两评价打分后，运用公式(1)整理为综合判断矩阵，如表4所示：

Table 4. Judgment matrix for comprehensive evaluation of the feasibility of project investment decision-making

表4. 项目投资决策可行性综合评价判断矩阵

在得到综合判断矩阵后，笔者利用MATLAB2017软件求出准则层特征向量 $W={\left(0.707,1.414\right)}^{\text{T}}$ 和准则层最大特征根 ${\lambda }_{\max }=2$。依照前文所述一致性检验方法，分别计算CI和CR值。最终对照平均一致性指标表(表3)确定判断矩阵S具有满意一致性特征。指标层处理过程与方法同准测层类似，本文在此不做过多赘述。项目投资决策可行性综合评价结果，如表5所示。

Table 5. Comprehensive evaluation results

表5. 综合评价结果

4.3.2. 结果分析与建议

经过模糊层次分析法的计算，可得出项目财务投资决策的综合指标体系：

$\begin{array}{c}\text{P}\text{.I}\text{.}=\left(-8.28\%\right)\ast 投资回收期+6.89\%\ast 投资回报率+37.56\ast 净现值\\ +12.55\%\ast 获利指数+34.72\%\ast 修正内部报酬率\end{array}$

其中，由于投资回收期年限越短越倾向于接受该项目，所以赋予该指标负权值。

从准则层来看，静态投资决策指标虽然计算过程相对简单，但只能在相同或类似并购案例之间进行比较分析；动态投资决策指标通过复杂运算，与时间价值原理紧密相连，可以更好地指导项目长期运营。结合权重系数来看，动态决策指标较静态决策指标所占权重更大。在企业实际工作中，应建立两种投资指标配合使用，相互补充，以动态指标为主，静态评价指标为辅的行动指南。

进一步考量指标层，净现值(NPV)和修正内部报酬率(IRR^*)的总体贡献更加显著，并且净现值指标要优于内含报酬率指标。这两种指标都考虑了时间价值因素，在面对不同投资者的不同投资需求时，又根据自身指标的特点给与了相应的参考。但是事实上，正如笔者在上面段落中所提到的两种指标可能在一定情况下会产生矛盾的结果，所以在进行投资决策时，投资者需要根据实际情况综合分析，在切实的场景中适时调整，而并不应仅仅依靠单一指标进行决策。两种指标存在的最大差异是再投资报酬率的选择，根据微观经济学原理，投资项目的边际收益是逐步递减的。在充分竞争的市场条件下，如果内部报酬率以超过资本成本的现有项目报酬率作为再投资决策，必然会违背经济规律，甚至高估投资项目的效益。修正内部报酬率虽然克服了该因素的影响，但专家的历史经验判断会造成两指标选用间存在细微差距。

当然，该综合评价指标体系只是从财务盈利能力的视角进行决策，项目投资还需要考虑风险因素、偿债能力指标和营运能力指标等，只有对自身将要投资的项目进行深入分析研究，才能系统化、全面化的进行项目投资效益评估。