轴流风机非稳态气动声学建模及分析

Modeling and Analysis of Unsteady Aeroacoustics of Axial Fan

摘要: 轴流风机作为应用广泛的流体机械，其声学性能逐渐受到人们重视。本文以某轴流风机为研究对象，结合计算流体力学和计算气动声学理论对轴流风机的声场进行数值模拟，利用雷诺时均(RANS)模型进行稳态流场模拟，通过在风机进口、出口和叶片表面上布置监测点，研究了风机在近场流域内的声源分布特性及声场变化趋势；利用大涡模拟(LES)非稳态流场和Ffowcs Williams-Hawkings声类比模型结合的方法，通过在风机流场外设置声接收器，对流域外的声场进行积分预测，同时，本文进行了相关实验，验证了数值仿真的准确性。研究发现，轴流风机的主要噪声来自偶极子源，主要原因是由于压力梯度的变化；近场中，风机的噪声在靠近叶片的地方出现相对较大的声压，噪音通过远距离的传播，声压在全频段上整体减小，但衰减趋势不变。

Abstract: As a widely used fluid machinery, the acoustical performance of axial flow fans has been paid more and more attention. In this paper, an axial fan is taken as the research object, and the sound field of the axial fan is numerically simulated by combining computational fluid dynamics and computational aero-acoustics theory to obtain the sound source distribution and acoustical law in the fan basin. The steady-state flow field was simulated by using the Reynolds time-mean (RANS) model. By setting monitoring points on the inlet, outlet and blade surface of the fan, the characteristics of the sound source distribution and the variation of the fan sound field in the near field basin were studied. By combining large eddy simulation (LES) unsteady flow with Ffowcs Williams-Hawkings acoustic model, the acoustic field was predicted through an acoustic receiver which was set up outside the fan flow field. Meanwhile, the accuracy of the numerical simulation was verified by relevant experiments. It is found that the main noise of axial fan comes from dipole source, which is mainly due to the change of pressure gradient. In the near field, the noise of the fan appears relatively large sound pressure near the blade. The noise propagates over a long distance, and the sound pressure decreases in the whole frequency band, but the attenuation trend remains unchanged.

1. 引言

轴流风机以流量大、耗电少的优势广泛应用于工业各领域中。但对有些工作环境恶劣的轴流风机，其内部易产生非稳态流动，从而引起振动、噪声等不良影响。随着计算流体力学(CFD)和计算气动声学(CAA)的不断发展，人们越来越多地着眼于轴流风机气动噪声的计算与优化。

目前，风机的噪声研究主要有实验测量和数值模拟的方法，在实验方面，Behdad Davoudi [1] 采用阵列测量的方法测出了轴流风机的10个不同位置的声学特性。杨野 [2] 等人搭建了风机噪声测量实验台，测得了轴流风机不同方位的远场噪声分布特性，并指出风机的进口噪声显著大于出口噪声。在数值模拟方面，2011年刘洪秋 [3] 等人对轴流风机旋转域内的非定常流动进行了数值计算，得到了风机的气动噪声源分布；李春曦 [4] 等人为研究叶片安装角对风机气动噪声的影响，对某型号轴流风机的噪声进行了三维数值模拟研究，得到了风机的声源分布和噪声特性。

本文结合数值分析和试验测试对某轴流风机进行噪声分析：通过由稳态向非稳态过渡的分析方法获取更可靠、有效的风机噪声分析结果并通过实验进行验证；另外，通过对近场和远场噪声的分析得出风机噪声源分布及传播特性，可为后续降噪设计奠定数值基础。

2. 模型建立

2.1. 风机模型

风机的基本几何参数如下：叶片数为4，半径为0.45 m，位于半径为0.5 m的圆柱中心；物理运动参数如下：转速为954 rpm，空气速度为3.4 m/s，温度为300 K。将整个系统分成三部分：进口区域、叶片旋转区域、出口区域，利用STAR-CCM + 专业流体分析软件对区域进行自动网格划分，为了提高计算效率，对于结构较简单的进、出口流域采用切割体网格并使用较大的网格尺寸进行有限元网格划分；对于旋转区域，由于叶片结构复杂需进行细致的网格划分：采用多面体网格进行体网格生成，并附加棱柱层边界网格以适应叶片表面的扭曲，如图1为划分好网格的叶片及风机系统；对于区域间的交界面均设置为interface边界用于相邻区域的参数传递。

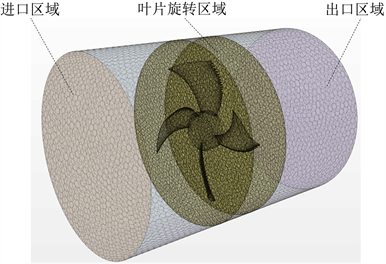
Figure 1. Grid of fan system structure

图1. 风机系统结构网格

2.2. 湍流模型

由于噪音的保真度与湍流模型建立有关，为节省算力，此处选择在稳态分析时使用雷诺时均(RANS)模型求解平均量来近似湍流波动的影响，在非稳态分析时利用尺度求解模型对关键湍流波动进行求解 [5]。

RANS模型 [6] 在求解平均动量和平均能量传输方程时，比起原始的纳维–斯托克斯(N-S)方程组会多出湍流应力张量 $T_{\text{RANS}}$ 使得控制方程不能封闭，为了封闭方程，引入涡流粘度μ_t概念建立平均量与应力张量的关系(式(1))，基于可压缩流和低雷诺数(Re = 4.3758e5)的流动，此处选用k-ω双方程对μ_t求解。

$\{\begin{array}{l}{T}_{\text{RANS}}=2{\mu }_{t}S-\frac{2}{3}\left({\mu }_t\nabla \cdot \bar{v}\right)I\\ S=\frac{1}{2}\left(\nabla \cdot \bar{v}+\nabla \cdot {\bar{v}}^T\right)\\ {\mu }_t=\rho kT\end{array}$ (1)

式中， $\bar{v}$ 为平均速度，I为单位张量，ρ为密度，k为湍动能，T为湍流时间尺度。

与RANS模型不同，尺度解析模型 [7] 将N-S方程组近似为对大尺度运动湍流的求解，为了求解关键性湍流结构，选用改进的大涡模拟(LES) [8] 对所求变量进行空间滤波，滤除与高频率相关的小涡流，用亚网格近似，从而缩小求解尺度范围。此时，在求解动量和能量传输方程时，多出的湍流应力张量表示已求解的大涡流与未求解的小涡流之间的相互作用亚网格尺度应力 $T_{\text{SGS}}$，同样为了封闭控制方程，使用WALE亚网格尺度对 $T_{\text{SGS}}$ 求解，见式(2)。

$\{\begin{array}{l}{T}_{\text{SGS}}=2{\mu }_{t}S-\frac{2}{3}\left({\mu }_t\nabla \cdot \bar{v}\right)I\\ S=\frac{1}{2}\left(\nabla \cdot \bar{v}+\nabla \cdot {\bar{v}}^T\right)\\ {\mu }_t=\rho {\Delta }^2{S}_W\end{array}$ (2)

2.3. 声学模型

由于稳态分析是为了粗略估计噪声的位置和强度，此处选择用宽频噪声源模型对轴流风机在RANS湍流中的运动进行声学建模，使用Curle积分和Proudman积分直接计算风机的偶极子源和四极子源 [9]。

Curle函数 [10] 用来估计偶极子宽频噪音源在体表面每单位面积的局部声功率(Surface Acoustic Power, SAP)对总声功率的贡献(式(3))；Proudman函数 [11] 用来估计四极子源的噪音源在流域内每单位体积的局部声功率(Volume Acoustic Power, VAP)对总声功率的贡献(式(4))。

$\text{SAP}=\frac{1}{{\rho }_0{a}_0}{\displaystyle {\int }_0^{2\text{π}}{\displaystyle {\int }_0^{\text{π}}\overline{{p^{\prime }}^2}}}{r}^2\sin \theta \text{d}\theta \text{d}\gamma$ (3)

$\text{VAP}={\alpha }_c{\rho }_0\frac{U^3}{L}\frac{U^5}{a_0^5}$ (4)

其中： $a_0$ 为远场声速，在300 K的的干燥空气中为347.2 m/s； ${\rho }_0$ 远场密度； $p^{\prime }$ 是声压；r为声源和流场某一位置的距离；θ为壁面法向和r的角度；γ是恒定压力和恒定体积下的比热容；α_c为重标系数 [12]，取α_c = 0.629；U为湍流速度；L为湍流长度标度， $L=k^{3/2}/\epsilon$ ；ε为耗散率。

对于非稳态分析，此处试图利用CFD/CAA耦合法计算近场声波，再用Ffowcs Williams-Hawkings (FW-H)这种空间和时间的高阶离散声模型 [13] 获取远场点的声压信息。

3. 稳态分析

气动声学本质上属于非稳态物理，但由于非稳态求解需要精细的网格来分辨与声学分析相关声源的频率，因此，需要先在稳态情况下对流场和声场进行求解，粗略估计噪声的位置并细化网格，当网格所能辨析的频率满足非稳态分析需求以后再利用FW-H声类比模型求解非稳态噪声分布特性。

宽带噪声源模型可通过RANS湍流时间长度和长度尺度的相关性提供气动声源的位置和能量信息，高声压区即为网格需要加密的地方；根据网格频率截止函数量化网格的适用性，确定网格加密的程度。应用Curle和Proudman积分求解得出的面噪声源和体噪声源声功率如图2所示，计算500步，残差0.001，两图显示了各向同性的湍流在边界表面和流域内产生的噪声级。

(a) (b)

Figure 2. Curle acoustic power per unit surface and Proudman acoustic power per unit volume. (a) Curle acoustic power per unit surface; (b) Proudman acoustic power per unit volume

图2. Curle单位表面积声功率和Proudman单位体积声功率。(a) Curle单位表面积声功率；(b) Proudman单位体积声功率

可以看出，由于叶轮尾缘顶尖和叶片迎风侧处是首先接触气流的部分，因此具有较大的Curle声功率，噪声水平大致为75~88 dB，叶片之外是气流分离区，气流接触壁面后受阻出现向自由流域扩散的涡流，噪声也集中在叶尖至旋转壁面之间的区域，噪声极值也出现在此区域的边界处，因此，上述部位需进行网格加密。

而对于网格加密的程度，Mendonça [14] 证明，由局部网格间距D合理求解的最大频率f_MC为：

$f_{MC}=\sqrt{\frac{2}{3}\bar{k}}/2D$ (5)

其中， $\bar{k}$ 表示平均湍流结构所含的平均湍动能。只要利用RANS模型求出非稳态纳维–斯托克斯(N-S)方程关于湍动能k的时均分量解，就可以获取平均湍流的特性。

如图3为叶片附近截面上的网格截止频率云图，在Proudman相关所指声源域内，网格最大可分辨出约916 Hz的声压，人类听力对1000~3000 Hz的声音最为敏感，因此，需细化网格扩大可求解的频率范围：通过不断调整计算，得出图4所示曲线，该曲线反映了在控制其他网格尺寸不变的情况下只改变叶片表面网格尺寸可以辨析出的最大网格截止频率值。

Figure 3. Mesh-frequency cutoff

图3. 网格截止频率

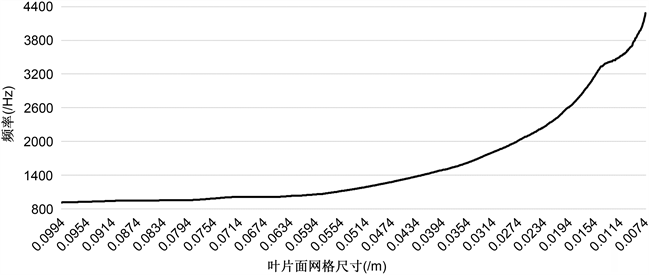
Figure 4. Blade surface mesh size and mesh-frequency cutoff

图4. 叶片表面网格尺寸与最大网格截止频率

经过多次调整，最终将叶片上的面网格尺寸控制在0.0074 m以保证非稳态分析3000 Hz以上的要求。最终划分好的进、出区域总网格单元数为95,581，旋转区域为3,898,677。

4. 非稳态分析

非稳态分析的边界条件和稳态分析一样，根据频率采样定理，采样频率定为2000 Hz，将每个时间步内的最大迭代次数设置为5次，整个模拟过程时间为0.3 s，由于流场需要一段时间稳定，所以从0.005 s开始记录FW-H非稳态求解器计算结果。

图5给出了叶片附近的压力云纹，可以看出在此截面处压力幅值大且分布不均，叶片周围压力梯度过渡较窄，这意味着叶片表面有较强的压力脉动，叶片周围气流紊乱且会产生较大冲击，从而引起大的噪音。同稳态分析的Proudman声功率对比可知，压力梯度大的部位也是噪声水平高的部位，而压力梯度小的部位，即使是压力幅值大噪声水平也不高，这说明决定噪声水平的是压力梯度而不是压力幅值。

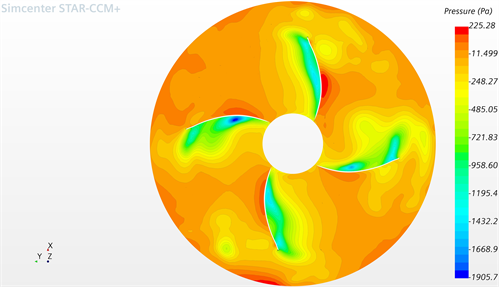
Figure 5. Pressure nephogram near blade

图5. 叶片附近压力云纹

为了观察风机内部压力波动情况和噪声水平，在风机系统内布置测点，图6显示了测点分布，近场设置三个测点，分别在入口流域和旋转区域的过渡处、叶尖处、出口流域与旋转区域的过渡处，进口测点和出口测点都在风机轴心线上，通过获取测点压力数据，利用快速傅里叶变换(FFT)可将声压级从时域转换到频域；在远场距叶片轴心线轴向、径向1 m处的位置布置接收器，应用FW-H对接收器获取的声源数据在时间域内积分，然后利用FFT处理得到接收器处的声频信息。

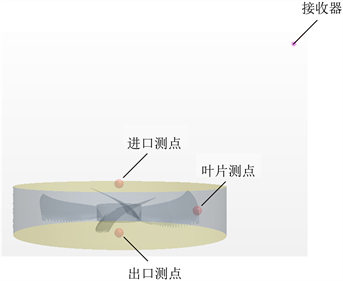
Figure 6. Distribution of fan measuring points and receivers

图6. 风机测点和接收器分布

如图7(a)为近场测点处声压对频率变化的情况，图中可以看出，进、出口的声压峰值均出现在6.7 Hz左右，叶片的峰值则出现在63.3 Hz处，叶片处的峰值声压最高为147 dB，进、出口处峰值相似约为120 dB，对照图5可以看出，随着压力梯度的增加，噪声也逐渐增加，而压力大的位置噪声并不一定大，这说明噪声的产生与空气流动的压力梯度有关而与压力大小不相关；随着测点与叶片距离的增加，噪声在低频段会有更大的衰减幅值，但峰值出现的频率却没太大的变化，这说明距离对风机噪声的影响是作用在整个频段的。

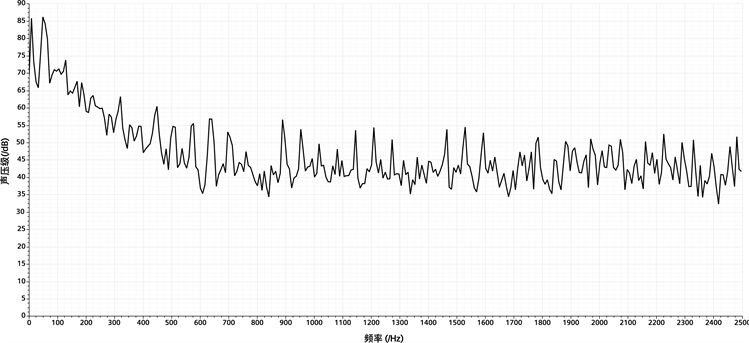(a)(b)

Figure 7. Frequency-sound pressure distribution. (a) Frequency-sound pressure of near field measuring points; (b) Frequency-sound pressure of front_1 m receiver

图7. 频率–声压分布。(a) 近场测点频率–声压；(b) 远场接收器频率–声压

图7(b)为远场接收器声压–频率变化图，从图中可以看出，声波经1 m的传播，最大噪声为85.77 dB，出现在50 Hz的频率处，且在此接收器处具有与近场测点相似的声压衰减趋势。不论是测点还是接收器，噪声的衰减都在低频段比较明显。

为验证数值仿真的有效性，针对研究模型进行了室内噪音测试，测试按照GB/T2888-2008 [15] 标准在，风机转速采用光电转速仪测量，噪声测量采用精度为0.5%的声级计，麦克风放置在风机出口距离轴心有1 m水平距离、与轴心线呈45˚俯角的位置，如图8显示了实验设备及具体布置。

Figure 8. Fan noise testing experiment

图8. 风机噪声测试实验

在转速为954 rpm的实验结果如图9所示，结果表明在0~4416 Hz频率段内的最大声压为84.5 dB。

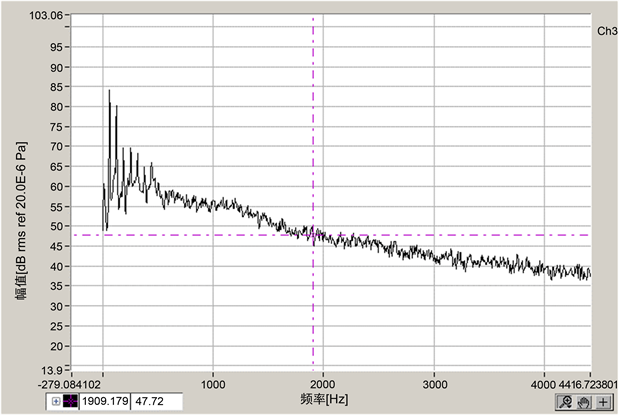
Figure 9. Spectrum diagram of measuring point

图9. 实验监测点频谱图

将实验结果与仿真结果进行对比，如图10所所示，可以看出，实验与仿真中噪声的变化趋势基本一致，最大声压级幅值的仿真误差为1.48%，在误差允许范围内，由此可验证数值仿真结果的可靠性。

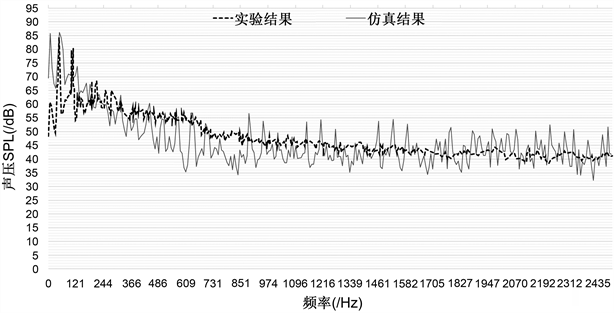
Figure 10. Comparison of test and simulation results

图10. 实验与仿真结果对比

5. 结论

通过对某轴流风机模型的流场、稳态声源和非稳态噪声进行数值仿真分析，设置测点观察近场噪音分布，布置接收器对噪音在远场的传播做了计算，并通过关联实验验证了此次研究仿真的可靠性。在此过程中，发现了空气流动对噪声源的分布和传播路径的影响，有以下几个方面：

1) 噪音源与空气流动压力梯度有关，此风机的噪声源以偶极子声源为主。

2) 通过对近场测点的声压提取，发现出口噪声水平普遍比进口处大，叶片噪声峰值出现的频率比流域内的高，距离会影响噪声衰减的幅值，但不会对噪声峰值出现的频率有太大影响。

3) 远场接收器的声压与进、出口测点的声压均反映出了风机噪声的频带叠加，即宽频带上叠加有离散的频带。宽频主要由气流造成，是声频图上平缓、宽阔的部分；离散频主要由叶片的旋转造成，是频谱图上离散的峰值。虽然风机的最大噪声处于叶片旋转噪声的基频处，但风机噪声中还是气动噪声的贡献最大。上述发现有助于风机噪声识别，可为后续降噪设计提供指导。

NOTES

^*通讯作者。