1. 引言
摄影测量卫星因覆盖范围广、不受地区和国界限制,逐渐发展成为重要的测绘手段 [1],与航空、陆基、海基、水下一起构建形成全维测绘体系。我国地幅辽阔、边境线长且地形复杂多变,很多地区必须依靠摄影测量卫星进行测绘作业。卫星摄影测量通常采取“全球连续覆盖”和“局部区域覆盖”两种摄影模式。“全球连续覆盖”模式卫星一般搭载三线阵CCD相机,采用推扫式成像,优点是覆盖范围广,缺点是受限于卫星平台稳定性,尤其是姿态稳定性,在无大地控制点地区,测量定位精度一直得不到保证 [2]。如何对测量误差进行高效补偿,提升定位精度一直是卫星无控测绘领域的一道难题。
文献 [3]、 [4] 对卫星摄影测量的关键技术进行了介绍,文献 [5] 从国家战略层面介绍了测绘行业的发展趋势,王任享院士研究了姿态低频误差的补偿技术 [6],文献 [7] - [12] 分别针对国内资源3号和天绘1号卫星提出了提高测量定位精度的方法,文献 [13] [14] [15] 重点研究了星敏感器的误差补偿技术,文献 [16] 分析了影像质量对定位精度的影响,文献 [17] 改进了影像处理的滤波方法和编辑方法,文献 [18] 对电离层延迟进行了建模和精度分析,文献 [19] 对比分析了星载线阵CCD相机与激光测高仪无控定位的精度,文献 [20] 提出采用激光测高仪提高测绘卫星的定位精度,文献 [21] 引入国外公开的卫星测量信息作为观测冗余量辅助国内卫星,提高测量定位精度。关于如何对误差进行处理,进而提高卫星测量精度的研究成果还有很多,因篇幅所限,本文只选取了比较有代表性的文献。误差的处理可以从误差源本身、误差的传递、误差的作用终端切入。本文从卫星测量定位原理出发,直观地分析了各误差源的生成原因和作用环节,定性估计了各误差源对终端测量定位精度的影响程度,并介绍了一些可行的误差处理方法,为想在此领域开展研究的学者提供一个清晰的理论参考。
2. 三线阵CCD相机成像原理
卫星三线阵CCD相机采用三镜头三线阵相机形式,其光线结构如图1所示。三镜头的三线阵构成一个相当于同一个框幅的像面,理论上三条光线相交于摄影中心,工程上因机械限制,只能相交于卫星飞行方向,扫描线方向上存在相交点偏差。三线阵CCD相机采用推扫式成像。前视、下视、后视三个CCD阵列相互平行,与飞行方向垂直。随着卫星平台移动,在
、
、
时刻,若前视、下视、后视分别通过中心投影方式得到的影像形成交会,意味着这三个时刻前视、下视、后视影像对应的是同一物方,即可通过联立共线方程组求解得到物方的空间坐标。
3. 主要坐标系及相关参数定义
方便起见,三线阵CCD相机成像中用到的主要坐标系和位置关系在图2中给出。图2中:
:数字影像坐标系,为平面坐标系,原点位于影像框幅左上角,
轴沿卫星飞行方向,
轴沿扫描线方向;
:传感器坐标系,原点位于线阵投影中心,
轴、
轴与数字影像坐标系平行,
轴按右手规则确定;
:卫星本体坐标系,原点位于卫星质心,
轴沿卫星纵轴指向卫星飞行方向,
沿卫星横轴,
按右手规则确定;
:星敏感器安装坐标系,原点位于卫星质心,
、
、
成右手规则;

Figure 1. The structure of the three-line CCD camera
图1. 三线阵CCD相机结构
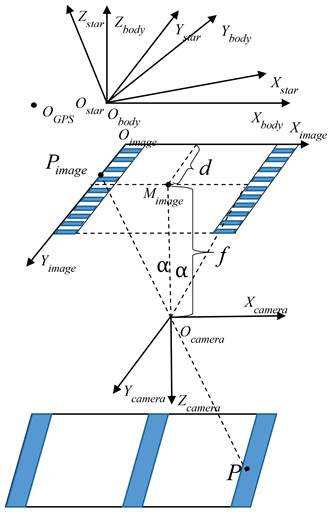
Figure 2. Main coordinate system and parameter definition
图2. 主要坐标系及参数定义
f:相机主距,设计上前视、下视和后视的相机主距应当满足
(下标
分别表示前视、下视和后视),但因工艺原因存在误差,三者并不完全一致;
a:交会角,设计上应当满足
,
,因工艺原因可能存在误差;
:用于卫星定轨的GPS相位中心;
:像主点,线阵投影中心
在数字影像坐标系上的投影,设计上应当满足
,
,
在一个点重合,但因工艺原因和机械限制,可能存在误差;
d:
距离数字影像坐标系
轴的距离。
4. 定位原理
如前所述,地物点的位置是通过前视、下视、后视的影像交会,联立共线方程组求解得到。
在同一坐标系下,共线方程可表示为:
(1)
其中:P为物方坐标;
为线阵投影中心坐标;
为像方坐标;
为比例系数,未知,是个标量;
表示
到P的向量,为矢量,后面内容中两个坐标点相减的表示与此类同。
从式(1)明显可以看出,共线方程的求解最关键的是确定
的空间位置,
的空间位置一旦确定,P与
即可形成明确的映射关系。
的空间位置包含两个方面,对于相机内部,称之为内方位元素,用主距f、像主点位置
、交会角a可确定;对于相机外部,称之为外方位元素,用传感器坐标系在地固坐标系中的位置和姿态角确定。内方位元素对应算式(1)等式右边,外方位元素对应式(1)等式左边。
考虑到卫星在轨运行时,
不能直接进行观测,只能通过卫星GPS相位中心的实测值与标定的GPS相位中心与卫星质心以及线阵投影中心与卫星质心的位置关系进行在线解算,故将式(1)转换为:
(2)
定义:
;
;
.
可以将式(2)简化为:
(3)
2008年7月1日起,我国全面启用2000国家大地坐标系,简称CGCS2000坐标系,所有的测绘成果都必须统一到该坐标系。因此,本文在CGCS2000坐标系下进行描述:
(4)
考虑到:
;
;
;
表示
坐标系,叫做协议天球坐标系,也称协议惯性坐标系,其与地球自转无关。Z轴指向北平天极,X轴指向平春分点,Y轴与Z、X成右手直角坐标系。C表示两个坐标系之间的转换矩阵。将
、
合并为
,即
,式(4)可转换为:
(5)
由于前视时,
(6)
下视时,
(7)
后视时,
(8)
将式(6)、(7)、(8)分别带入式(5),可以得到前视、下视、后视的共线方程:
前视:
(9)
下视:
(10)
后视:
(11)
式(9)、(10)、(11)中,相机主距
、
、
,交会角
、
(实际安装中,以下视为基准确定前后交会角,因此
),像主点位置参数
、
、
,为内方位元素,在地面试验室进行相机参数检校确定。GPS相位中心与摄影中心距离的
,
、
在地面试验室进行标校确定;
通过GPS接收机的观测值确定;
通过星敏感器拍摄的星图数据与星表进行匹配计算确定;
为
坐标系与CGCS2000坐标系的转换矩阵,可精确确定。
由式(9)、(10)、(11)明显可以看出,不管是前视、下视还是后视,已知物方坐标
,求解影像坐标都是三个方程解两个未知数:
和
。这就意味着这三个方程之间是存在相关性的,物方坐标须满足一定的条件才能成像,此外,受影像框幅(即
的幅值)限制,对物方坐标的要求又更加苛刻。
反之,已知影像坐标
,求解物方坐标
时,单独的前视、下视或后视影像坐标点,都无法得出物方坐标,原因是
未知,三个方程要解四个未知数:
和
,只能得出物方坐标在由
确定的这条直线上。前视、下视或后视任意两个影像坐标点联合都可以构成六个方程解五个未知数,解算出物方坐标。前视、下视和后视三个影像坐标点联合可以构成九个方程解六个未知数,在实际工程中,多出的冗余观测量往往都是为了降低各种误差的影响以提高精度。
5. 误差的作用环节及量级分析
经过以上分析已经知道了通过前视、下视、后视的影像交会联立共线方程组对地物点进行定位的基本原理。可以看出,影响定位精度的误差源主要来自三个方面:卫星本体包括相机的形变、传感器观测值本身的误差、匹配误差。
5.1. 形变误差
如上所述,相机主距(体现在共线方程的
、
、
项)、像主点位置(体现在共线方程的
、
、
项)、星载GPS相位中心与卫星质心距离和线阵投影中心与卫星质心距离(体现在共线方程的
项)等距离参数,交会角(体现在共线方程的
、
项)、星敏感器的安装姿态(体现在共线方程的
项)、相机的安装姿态(体现在共线方程的
项)等姿态参数,首先在地面试验室
进行标校确定,作为已知参数储存在星载计算机里。但是卫星入轨后,由于太空环境和地面试验室的不同,相机本身和卫星本体会发生微小形变,导致这些已知参数的实际值偏离标称值,产生误差。
误差量级分析:摄影测量卫星一般处在高度500公里附近的太阳同步轨道,在相机主距、像主点位置为米级时,从几何关系中可以清晰地看出,微米级的形变距离误差引起的定位误差约至米级,相机主距的误差传导至地物点坐标主要体现在高程误差,像主点位置的误差传导至地物点坐标主要体现在水平误差。星载GPS相位中心与卫星质心距离误差和线阵投影中心与卫星质心距离误差引起的定位误差与距离误差本身基本处于一个数量级。因形变产生的姿态误差对定位精度的影响非常大,粗算可知秒级的角度误差引起的定位误差就可达到米级,而且耦合性非常高。
5.2. 传感器观测误差
这部分误差主要包括星载GPS接收机的观测误差(体现在共线方程的
项),相机对地物点的拍摄精度(包含相机分辨率和大气环境、电离层等对光线传输的路径影响,体现在共线方程的
项),星敏感器的观测误差(体现在共线方程的
项)。
误差量级分析:星载GPS接收机的观测误差和相机对地物点的抓取误差基本与地物点的定位误差处于同一个数量级。星敏感器的观测误差直接作用于传感器坐标系与地固坐标系的姿态转换,对定位精度的影响非常大,秒级的角度误差即可引起米级的定位误差。
5.3. 匹配误差
主要包括两个方面,一是星敏感器拍摄的星图数据与星表进行匹配时产生的误差,体现在共线方程的
项;二是前视、下视、后视三个摄像头对抓取的地物点进行重合匹配时产生的误差,体现在式(9)、 (10)、(11)三组共线方程对应的地物点的重合程度。
误差量级分析:秒级的星图数据与星表的匹配角度误差可引起米级的定位误差。三个摄像头对地物点的匹配误差基本与定位误差处于同一个数量级。
6. 误差的处理思路
形变误差对定位精度的巨大影响一直是摆在卫星摄影测量领域的一个大难题。解决思路主要有以下二种:一是利用地面试验场对形变误差进行在轨标定,考虑到形变误差具有慢时变特征,可利用在轨标定结果对误差进行分析建模,找出变化规律,缺点是受制于地面试验场的分布区域和范围,误差的建模精度不高;二是硬件改进,例如材料改进、提高工艺水平、加长相机主距长度等,这是最能治根治本的方法,同时也是难度最大的。星载GPS接收机的观测误差主要是由于电离层影响,采用双频接收机可有效降低误差,目前双频接收机的误差可控制在分米级,此外,采用激光测距仪也可有效降低误差。相机的拍摄精度可以通过提高镜头分辨率以及图像处理方法的改进进行提升。星敏感器的观测误差主要通过地面试验场的在轨标定数据进行分析建模处理。匹配误差主要通过匹配算法的改进进行处理。
此外,也可以在定位端引接其它辅助信息用以提高定位精度。一是用大地控制点进行平差处理,这是最直接有效的方法,难点在于控制点的布设受国界、区域、地形限制,境外区域、森林、沙漠、海洋等地区的控制点很少;二是用高程信息进行定位修正,但是受高程数据库的覆盖范围和精度限制;三是用激光测距仪进行定位修正,但是激光测距仪的安装会增加卫星的载荷重量;四是多卫星联合摄影测量,通过增加观测冗余量以提高定位精度,受卫星的数量和扫描区域限制。
7. 结论
测绘产品保障一直是部队作战筹划、兵力行动、武器平台运用的重要支撑。一方面,随着武器装备的精细化发展和高精导武器的大量运用,对地形图、三维场景、数字影像等产品的精度提出了越来越高的要求;另一方面,随着“军事力量走出去”、“一带一路”国家战略发展,迫切需要边界、境外重要地区和敏感地区的测绘产品保障。常规空基、陆基、海基、水下测绘手段已经远远不能满足日益增长的作战需求,急需卫星测绘的大力发展以形成全球测绘能力。高效降低误差影响,提高测量定位精度需要定轨、导航、遥感、信号处理、图像处理、材料、机械、空间环境等各专业领域人士的通力合作。本文从基本的共线方程入手,介绍了卫星三线阵CCD相机的成像原理和定位原理,分析了各种误差的作用环节和效能影响,为在此领域正在开展或即将开展研究的学者提供了一个直观清晰的理论参考,同时也介绍了一些现行或可行的解决思路供读者参考。