基于集合平滑器的地下水污染源与含水层参数的同步反演

Simultaneous Identification of Groundwater Contaminant Source and Aquifer Parameters Based on Ensemble Smoother

摘要: 当地下水污染发生时，能够准确及时地得到污染源信息及场地的渗透性分布，对于污染修复方案的制定尤为重要。但这些信息无法直接观测获取，只能通过有限的观测数据来推估。本文利用集合数据同化方法ILUES算法作为求解框架进行地下水污染源与含水层参数的同步反演，重点探讨样本集合数目和观测信息对地下水污染源反演和含水层渗透系数场估计结果的影响。算例结果表明，融合观测水头数据和浓度数据的ILUES算法框架能够实现污染源参数和渗透系数场的同步反演；作为数据同化方法，ILUES算法参数(集合样本数量)和观测信息(观测井数量和空间分布等)都直接影响着地下水污染源反演和渗透系数场估计的准确性。

Abstract: When groundwater pollution occurs, it is particularly important to be able to obtain accurate and timely information on the source of contaminant and the hydraulic conductivity field of the site for the development of contamination remediation plans. However, this information cannot be obtained by direct observation and can only be deduced by limited measurement data. In this paper, the ensemble data assimilation method (ILUES algorithm) is adopted as the solution framework for simultaneous identification of groundwater contaminant source and aquifer parameters, the influence of sample set number and observation information on groundwater contaminant source identification and estimation of aquifer hydraulic conductivity field is discussed. The results show that the ILUES algorithm framework, which assimilates the observation data (hydraulic head and concentration data), can achieve the simultaneous inversion of contaminant source parameters and hydraulic conductivity field. As a data assimilation method, ILUES algorithm parameters (the number of ensemble samples) and observation information (the number and locations of monitoring wells, etc.) directly affect the accuracy of groundwater contaminant source identification and hydraulic conductivity field estimation.

1. 引言

目前，我国地下水污染已十分严重。由于地下水系统固有的复杂性、隐蔽性，地下水一旦遭受污染，不仅难以发现，而且治理和修复需要很长的时间 [1]。为了更好地管理地下水以及评价地下水污染的环境风险，通常需要先大致弄清污染源的情况，包括污染源分布以及污染浓度排放情况等，该过程被称为地下水污染源反演 [2]。同时，进入地下水系统的污染物受含水层非均质性影响，随着水流运动，在迁移扩散和各种物理化学过程作用下，呈现非均质分布特征，因此需要准确掌握含水层参数信息(渗透系数、弥散度等)，该过程被称为含水层参数反演 [3] [4]。

地下水污染源反演和含水层参数反演都属于地下水逆问题，数据同化方法已成为求解地下水逆问题的重要方法 [5] [6]。数据同化是通过融合真实的观测数据和数值模型的预测数据，从而实现对系统参数和状态的可靠估计 [7] [8]。基于集合的数据同化方法是目前常用的数据同化方法，如集合卡尔曼滤波器(EnKF)和集合平滑器(ES)。与需要同时更新模型参数和状态的EnKF相比，ES仅更新参数，避免了EnKF中观察到的更新参数和状态之间的不一致问题 [9]。研究表明，在处理高维强非线性问题时，标准ES算法通常难以获得令人满意的参数反演结果，Ju等 [10] 将IES与高斯过程替代模型结合，高效准确地识别了非均质渗透系数场。Zhang等 [11] 提出了一种迭代局部更新集合平滑器(Iterative Local Updating Ensemble Smoother, ILUES)，进一步提升ES在非线性问题中的适用性和运行效率。

作为数据同化方法，算法参数(集合样本数目 $N_e$ 等)会对逆问题求解效率产生一定的影响 [12]。同时，观测数据作为反演问题求解的关键信息来源，观测井数目和空间分布等会影响到各种观测信息中的信息量，进而对反演结果的准确性也会产生重要的影响 [13] [14] [15]。基于前人研究，本文利用集合数据同化方法ILUES算法作为求解框架，重点探讨样本集合数目和观测信息(观测井数目和空间分布等)对地下水污染源反演和含水层渗透系数场估计结果的影响，实现地下水污染源与含水层参数的同步反演。

2. 同步反演优化模型

地下水污染源和含水层参数的同步反演问题是通过使观测点的实测值和模拟值偏差达到最小从而获取地下水污染源信息(污染源位置、污染物排放浓度、排放时间等)以及未知含水层参数(渗透系数、弥散度、有效孔隙度等)。同步反演模型包括模拟模型(地下水污染迁移模型)和逆问题的求解框架(直接法、优化方法、数据同化方法等)，本文采用集合数据同化方法ILUES算法作为逆问题的求解框架。

2.1. 地下水污染迁移模型

目前常用的污染物迁移模拟程序有MT3DMS、RT3D、PHT3D、FEFLOW等。其中，MT3DMS是应用最为广泛的污染物迁移模拟程序。本文采用MT3DMS程序进行地下水污染物迁移模拟。MT3DMS本身不包括地下水流模拟程序，计算模拟需和MODFLOW联合使用。

MODFLOW的地下水流方程如下 [16]：

$\begin{array}{c}\frac{\partial }{\partial x}\left(K_{xx}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left(K_{yy}\frac{\partial h}{\partial y}\right)+\frac{\partial }{\partial z}\left(K_{zz}\frac{\partial h}{\partial z}\right)+W=S_s\frac{\partial h}{\partial t}\end{array}$ (1)

式中，假定渗透系数主轴方向与坐标轴方向一致， $K_{xx}$、 $K_{yy}$、 $K_{zz}$ 分别为渗透系数在x、y、z方向上的分量，m/d；h为水头，m；W为单位时间从单位体积含水层流入或流出的水量，1/d； $S_s$ 为孔隙介质的贮水率，1/m；t为时间，d。

MT3DMS的地下水溶质运移方程如下 [17]

$\frac{\partial \left(\theta c^k\right)}{\partial t}=\frac{\partial }{\partial x_i}\left(\theta D_{ij}\frac{\partial c^k}{\partial x_j}\right)-\frac{\partial }{\partial x_i}\left(\theta v_i{c}^k\right)+q_s{c}_s^k+{{\displaystyle \sum }}^{\text{}}{R}_n$ (2)

式中， $\theta$ 为含水介质的孔隙度，无量纲； $c^k$ 为溶质组分k的浓度，g/m³； $D_{ij}$ 为水动力弥散系数张量，m²/d； $v_i$ 为含水介质中的实际水流速度，m/d，与Darcy流速 $q_i$ 的关系为 $v_i=q_i/\theta$ ； $q_s$ 为单位体积含水层的源汇项流量，1/d； $c_s^k$ 为源汇项中溶质组分k的浓度，g/m³； ${{\displaystyle \sum }}^{\text{}}{R}_n$ 为化学反应项总和，g/(m³d)。

2.2. 逆问题的求解框架

假设观测数据与模型参数之间的关系可表示为：

$d=f\left(m\right)+\epsilon$ (3)

式中， $d$ 是测量值， $f(\cdot )$ 是正演模拟模型， $m$ 是未知模型参数向量， $\epsilon$ 是观测误差向量。

集合平滑器(ES)通过同化观测值 $d$ 以更新未知模型参数：

$m_j^a=m_j^f+C_{MD}^f{\left(C_{DD}^f+C_D\right)}^{-1}\left[d_j-f\left(m_j^f\right)\right]$ (4)

式中， $M^f=\left[m_1^f,\cdots ,m_j^f,\cdots ,m_{N_e}^f\right]$ 是先验参数样本集合， $M^a=\left[m_1^a,\cdots ,m_j^a,\cdots ,m_{N_e}^a\right]$ 是更新后的模型参数样本集合， $C_{MD}^f$ 是先验参数样本集合 $M^f$ 和模型预测值样本集合 $D^f=\left[f\left(m_1^f\right),\cdots ,f\left(m_j^f\right),\cdots ,f\left(m_{N_e}^f\right)\right]$ 的互协方差矩阵， $C_{DD}^f$ 是 $D^f$ 的自协方差矩阵。

当未知模型参数 $m$ 的先验分布或后验分布非高斯分布时，无法直接用公式4对参数进行更新。不同于标准ES在更新过程中利用了集合中的所有 $N_e$ 个样本，迭代局部更新集合平滑器(ILUES)提出了局部更新的策略：1) 通过局部集合指标(公式5和公式6)确定样本集合 $M^f$ 中每个样本 $m_j^f$ 的局部样本集合；2) 对 $N_e$ 个局部样本集合分别利用公式4进行更新；3) 分别从更新后的 $N_e$ 个局部样本集合中随机选取一个样本，组合成更新后的整体集合 $M^a=\left[m_1^{loc,a},\cdots ,m_j^{loc,a},\cdots ,m_{N_e}^{loc,a}\right]$。

$J\left(m\right)=\frac{J_1\left(m\right)}{J_1^{\max }}+\beta \cdot \frac{J_2\left(m\right)}{J_2^{\max }}$ (5)

$N_l=\alpha N_e\left(\alpha \in \left(0,1\right]\right)$ (6)

式中， $J_1\left(m\right)$ 是模型输出 $f\left(m\right)$ 和观测值 $d$ 之间的距离， $J_2\left(m\right)$ 是模型参数 $m$ 和样本 $m_j^f$ 之间的距离， $\beta$ 因子表示两个距离度量在综合度量中的相对权重。 $J_1^{\max }$ 和 $J_2^{\max }$ 分别是 $J_1\left(m\right)$ 和 $J_2\left(m\right)$ 的最大值。样本集合 $m_j^f$ 的局部集合是具有最小 $J$ 值的 $N_l$ 个样本， $\alpha$ 因子是局部样本集合占全局样本集合的比例。上述局部更新算法可以通过简单的迭代过程反复调用，直至达到预设的收敛指标(相邻迭代步的样本集合差异足够小，或达到最大允许迭代次数等)。

3. 算例研究

3.1. 问题概述

如图1所示，考虑某非均质各向异性承压含水层，含水层水流运动为稳定流。研究区大小为15 m × 15 m，离散为60行60列的有限差分网格(网格初始尺寸为0.25 m × 0.25 m)。含水层厚度为1 m。南北边界为二类隔水边界，东边界为定水头边界(水位为5.25 m)，西边界为定水头边界(水位为6 m)，无其他源汇项。含水介质孔隙度为0.30，纵向弥散度为1.00 m，水平横向弥散度为0.10 m。含水层渗透系数K满足对数正态分布，其均值( $\overline{\ln K}$ )与方差( ${\sigma }_{\ln K}^2$ )分别为2.0和0.5，x和y方向的相关长度分别为4.0 m和2.0 m，变差函数为指数型。

初始时刻，含水层中无污染物。假设研究区存在三个潜在污染源S₁、S₂和S₃ (如图1)，污染物为保守型，并假设污染物不会对地下水流场产生影响。潜在污染源发生持续泄露(真实污染位置在S₁和S₃处)造成地下水污染，污染源释放强度非恒定，每个潜在污染源表征为10个未知参数进行量化，即10个应力期对应的污染源强度。假设污染源强度的先验分布是均匀分布，污染源参数的真实值和取值范围见表1。

考虑对空间上连续变化的渗透系数场进行反演时，渗透系数场的维度与模型的网格剖分程度有关(本算例为3600维)。高维地下水逆问题的求解效率较低，一般需要对渗透系数场进行降维，这里采用Karhunen-Loève展开的方法对渗透系数场进行降维 [18]。

$\ln K\left(x,y\right)\approx \overline{\ln K}\left(x,y\right)+\underset{i=1}{\overset{N_{KL}}{{\displaystyle \sum }}}{\xi }_i\sqrt{{\tau }_i}{s}_i\left(x,y\right)$ (7)

式中， ${\xi }_i$ 是独立标准高斯分布的随机数； ${\tau }_i$ 和 $s_i\left(x,y\right)$ 是特征值和特征函数； $N_{KL}$ 是Karhunen-Loève展开的项数。本算例中选择 $N_{KL}=400$，可以保留约95.20%的渗透系数场的变异性。

因此，本算例共有30个未知污染源参数和表征渗透系数场的400个KLE参数，共计430个未知参数需要反演计算。30个污染源参数的真实值见表1，渗透系数真实场如图1所示。为了估计这些未知参数，在研究区布设15个观测井(如图1)。本算例观测点的水头观测和浓度观测值是利用MODFLOW和MT3DMS事先计算得到，后续加入观测噪声作为观测资料。模拟时段总时长为160天，共10个应力期(每个应力期16天)。由每个应力期末时刻的模拟值和正态分布的测量噪声(公式8)计算得到观测值。

$c{h}_{obs}=c{h}_{simu}+c{h}_{simu}\times L\times \delta$ (8)

式中， $c{h}_{simu}$ 表示模拟值(水位或浓度)， $c{h}_{obs}$ 为观测值(水位或浓度)， $L$ 为噪声水平(取5%)， $\delta$ 为满足标准正态分布的随机偏差。

Figure 1. Plan of aquifer structure

图1. 含水层结构平面图

Table 1. The true value and prior range of releasing intensity of groundwater contaminant source

表1. 地下水污染源释放强度真值和先验范围

3.2. 结果与讨论

为了定量评价ILUES算法的参数估计效果，采用均方根误差(Root Mean Square Error, RMSE)和平均集合离散度(Average Ensemble Spread, AES)作为定量评价指标。RMSE用来度量待估计参数的估计值和真实值之间的接近程度，RMSE值越低，则参数反演精度越高。AES反映的是参数集合相对于估计值均值的离散程度，即参数估计值的不确定性。二者公式如下：

$\text{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left[{\left(V_e\right)}_i-{\left(V_a\right)}_i\right]}^2}{N}}$ (9)

$\text{AES}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N\left\{{{\displaystyle \sum }}_{j=1}^{N_e}{\left[{\left(V_e\right)}_{ij}-{\left({\hat{V}}_e\right)}_i\right]}^2\right\}}{N}}$ (10)

式中， $V_e$ 和 $V_a$ 分别代表第i个反演参数的估计值和真实值， ${\hat{V}}_e$ 代表第i个反演参数的估计值均值，N为待估计参数的总数， $N_e$ 为集合样本数量。

3.2.1. 集合样本数量的影响

作为数据同化方法，ILUES的算法参数的集合样本数量 $N_e$ 影响着逆问题的求解效果。基于上述算例，固定其他算法参数( $\alpha =0.1$ 和 $\beta =1.0$， $iter=7$ )，选用不同的集合样本数量( $N_e=1000,2000,3000,4000$ )，比较不同集合样本数量 值情况下的反演结果。

图2为不同 $N_e$ 值下的渗透系数场的估计结果，可以看出，4组渗透系数估计场在轮廓上都较好的反映了 $\ln K$ 场的形态以及高低值区域，但是在细节上随着 $N_e$ 值从1000增加至3000，估计得到的渗透系数场与真实场越来越相似(图2(b)~(d))，说明利用ILUES算法进行参数估计的过程中，更大的 $N_e$ 值能够更好地表征渗透系数场；继续增加 $N_e$ (从3000增至4000)渗透系数场的估计效果没有明显的提升(图2(d)和图2(e))，说明 $N_e=3000$ 经过7次迭代后，渗透系数场估计的不确定性(估计方差)达到很低的水平，已很难对反演结果进行提升。

Figure 2. Estimation of hydraulic conductivity field under different N_e values

图2. 不同N_e值下渗透系数场的估计结果

图3为不同 $N_e$ 值下的RMSE和AES值的变化趋势图。在污染源反演方面，ILUES算法 $N_e$ 从1000增至4000时，识别结果的RMSE值由0.8194降至0.4632 (降幅为43.47%)；对渗透系数场估计结果而言，渗透系数场估计结果的RMSE值由1.7234降至1.2533 (降幅27.28%)。同时，AES值在 $N_e$ 从1000增加至2000时迅速减小，而 $N_e$ 继续从2000增至4000时，污染源反演结果和渗透系数场估计的AES值无明显变化趋势；当 $N_e$ 达到4000时，污染源反演结果和渗透系数场估计的AES值分别为0.0965和0.4085，表明经7次迭代后验集合样本的离散度达到较低水平。

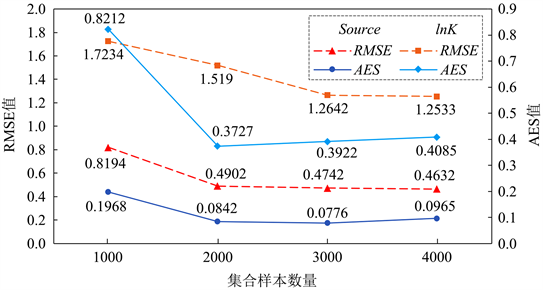
Figure 3. Trends of RMSE and AES values under different N_e values

图3. 不同N_e值下的RMSE和AES值的变化趋势图

考虑到随着 $N_e$ 的增加，运算时间和计算结果的存储空间都会显著增加。因此，为了平衡计算效率与计算精度，选择 $N_e=3000$ 为最佳样本集合大小。

3.2.2. 观测信息的影响

在ILUES算法中，参数反演时需要结合模型融入观测信息。上一节讨论了集合样本数量 $N_e$ 值对反演结果的影响，并确定了本算例的最佳集合样本数量 $N_e=3000$。在此基础上开展观测信息(观测井数量和空间分布等)对反演结果准确性的影响。为了探究观测井分布对地下水污染源反演和渗透系数场估计的准确性的影响，设置3种分布情形(图1，图4(a)和图4(b))，分布采用ILUES算法进行污染源参数及渗透系数场的反演。ILUES算法参数设置为： $\alpha =0.1$ 和 $\beta =1.0$， $iter=7$， $N_e=3000$。在3种观测分布中，形成2个对照组：1) 对照组1：图1和图4(a)为观测井数目相同(15个)但分布不同的情形，前者的观测井位置是随机分布于场地内，后者则是均匀分布于场地内；2) 对照组2：图1和图4(b)都是观测井位置随机分布于潜在污染源下游方向，但是观测井数目不同，前者为15个，后者为30个。

图5为3种观测分布下的污染源强度的反演结果(从表征污染源信息的30个未知参数分别选取了S₁的 ${\text{S}}_{\text{S1}}^2$、 ${\text{S}}_{\text{S1}}^9$，S₂的 ${\text{S}}_{\text{S2}}^2$、 ${\text{S}}_{\text{S2}}^9$，S₃的 ${\text{S}}_{\text{S3}}^2$、 ${\text{S}}_{\text{S3}}^9$ )。图6为不同观测分布下渗透系数场的估计结果(均值场和方差场)。

1) 对照组1：观测井数目相同(15个)但分布不同的情形

图5(a)和图5(b)是15个观测井均匀分布和随机分布情形下的污染源反演结果，可以看出：经过7次迭代后，两种分布情形下S₂的污染源反演强度均接近于0表明S₂处无污染发生，与实际情况相符；对于S₁和S₃，污染源参数样本收敛并接近于真实值，且随机分布情形下(图5(b))的反演结果优于均匀分布的情形。

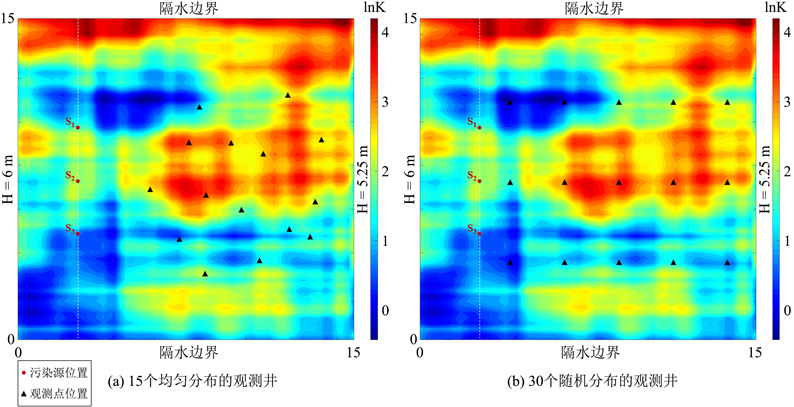
Figure 4. Sketch map of locations of monitoring wells

图4. 观测井空间分布示意图

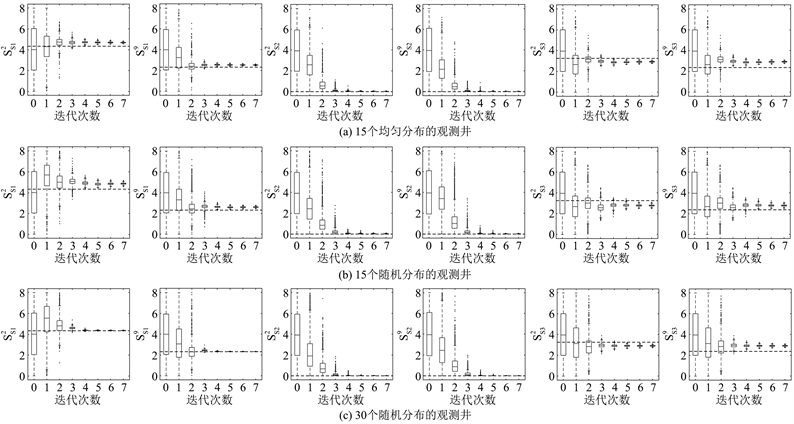
Figure 5. Inversion results of groundwater contaminant source intensity at different locations of monitoring wells

图5. 不同观测位置分布下的污染源强度的反演结果

图6(b)，图6(e)和图6(c)，图6(f)是从渗透系数场的反演估计结果探究观测井数目相同但分布不同(即对照组1)对ILUES算法反演结果的影响。两种情形的均值估计场(图6(b)和图6(c))都能够大致刻画出渗透系数场的形态及高低值区域，但是明显可以看出，利用随机分布的观测数据得到的均值估计场(图6(c))更接近于真实场(图6(a))，更准确地表征渗透系数场的中间大部分区域。渗透系数的估计方差场反映了集合的离散性(即估计的不确定性)，均匀分布的估计方差场结果(图6(e))略优于随机分布的情形(图6(f))，分析原因在于随机分布的观测井(图1)主要分布于潜在污染源下游方向，在场地边缘区域没有观测井，无法提供信息用于数据同化，因此在这些位置的渗透系数的估计结果存在着不确定性。但是总体而言，观测井数目相同(15个)随机分布情形下的污染源反演和渗透系数场估计效果更好。

2) 对照组2：观测井随机分布于潜在污染源下游方向，但是观测井数目不同的情形

图5(b)和图5(c)是利用随机分布的15个或30个观测位置的水头和浓度数据得到的参数反演结果，明显可以看出：采用30个观测位置识别的样本集合参数平均值更接近于真值，且收敛效果大大提高。对比图6(a)，图6(c)，图6(d)可以看出，ILUES算法通过同化15个观测位置的观测数据，渗透系数的均值估计场大致刻画出场地渗透系数场的主要形态和轮廓；利用30个观测位置的观测数据得到的估计均值场对高低值区域的刻画则更为准确；同时后者的估计方差场(图6(g))整体上低于前者(图6(f))，表明后者渗透系数场的估计结果不确定性程度更低。因此，观测井随机分布的情况下，观测井数目的增加明显有助于ILUES算法更为准确地实现地下水污染源反演和渗透系数场估计。

Figure 6. Estimation results of hydraulic conductivity field at different locations of monitoring wells

图6. 不同观测位置分布下渗透系数场的估计结果

4. 结论

1) 本研究利用集合数据同化方法ILUES算法进行地下水污染溯源和渗透系数场反演研究。ILUES算法参数(集合样本数量 $N_e$ )影响着地下水污染源反演和渗透系数场估计的求解效果。综合考虑计算效率和计算精度，确定 $N_e=3000$ 为最佳样本集合大小。

2) 观测信息(观测井数量和空间分布等)直接影响着ILUES算法估计参数的准确性。一般情形下，观测点数量越多，能够提供更多的信息用于数据同化计算，ILUES算法能够得到更准确的参数反演估计结果；在观测点数量相同的情况下，选取能够更多反映地下水位和浓度变化情况的观测点，将有助于获得更好的污染源反演和渗透系数场估计结果。

3) 不同观测位置在不同时刻的水位和浓度数据能够提供的信息量是不同的，影响着数据同化方法(比如ILUES算法)的参数估计结果。因此，考虑时间和成本，后续应进行优化观测井设计以选取最优观测位置，从而为数据同化方法提供信息量最大的观测信息。

基金项目

国家自然科学基金(42077176)；南京水利科学院水文水资源与水利工程科学国家重点实验室重点基金项目(2019nkzd01)；上海市自然科学基金资助项目(20ZR1459700)。

NOTES

^*通讯作者。