G 与 K₂ 的联图的局部反魔幻着色数

The Local Antimagic Chromatic Number of the Join Graphs G ∨ K₂

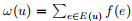
摘要: 令 G = (V, E) 是具有 n 个点、m条边的连通简单图。称图 G 是局部反魔幻的，则 G 有—个局部反魔幻标号。图 G 的局部反魔幻标号是—个双射 f : E → {1, 2, · · · , m}，使得对图 G 的任意两个相邻的顶点 u 和 v 都有ω(u) ≠ω(v)，其中,  E(u) 是与点 u 相关联的边的集合。若对图 G 的点 v 着颜色 ω(v)，明显得出 G 的任—个局部反魔幻标号导出图 G 的—个正常点着色。图 G 的局部反魔幻着色数是其局部反魔幻标号中所用的最少颜色数，记为 χ_la(G)。给定两个点不交的图 G 和 H，图 G 和 H的联图，记为 G ∨ H，是在图 G 和 H 的基础上，再将 G 的每—个点与 H 的每—个点相连而得到的图。本文给出了路 Pn，圈 Cn，星图 Sn以及友谊图 Fn与完全图 K₂ 的联图的局部反魔幻着色数的确切值。

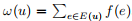
Abstract: Let G = (V, E) be a connected simple graph with |V | = n and |E| = m. A graph G is called local antimagic if G has a local antimagic labeling. A bijection f : E → {1, 2, · · · , m} is called local antimagic labeling if for any two adjacent vertices u and v, we have ω(u) ≠ ω(v), where , and E(u) is the set of edges incident to u. Thus any local antimagic labeling induces a proper vertex coloring of G, where the vertex v is assigned the color ω(v). The local antimagic chromatic number, denoted by χ_la(G), is the minimum number of colors taken over all colorings induced by local antimagic labeling of G. Let G and H be two vertex disjoint graphs. The join graph of G and H, denoted by G ∨ H, is the graph whose vertex set is V (G) ∪ V (H) and its edge set equals E(G) ∪ E(H) ∪ {ab : a ∈ V (G) and b ∈ V (H)}. In this paper, we give the exact value of the local antimagic chromatic number of the join graph G ∨ K₂, when G is paths Pn, cycles Cn, the stars Sn, the friendship graphs Fn, respectively.