基于AHP和DEA模型的物流中心绩效评价

Performance Evaluation of Logistics Center Based on AHP and DEA Model

摘要: 物流中心绩效是选址物流中心的一个重要考量标准，绩效是否符合预期目标直接关系到企业各项经营成本及其获利程度。本文结合数据包络分析法和层次分析法，建立了包括客观实际数据、带有输出偏好锥的数据以及对评价对象赋予权重的数据的数学模型，并根据计算结果对物流中心进行了综合评价和排序，从中选择出最优物流中心。在最后，以某区域物流中心的绩效评价作为案例，得出这一方法的适用性。

Abstract: The performance of logistics center is an important criterion for selecting logistics center. Whether the performance meets the expected target is directly related to the enterprise’s operating costs and profitability. In this paper, combining data envelopment analysis and analytic hierarchy process (AHP), a mathematical model which includes objective data, data with output preference cone and data given weight to the evaluation object is established. It makes a comprehensive evaluation and ranking of logistics centers according to the calculation results, and selects the optimal logistics center. Finally, the applicability of this method is obtained by taking the performance evaluation of a logistics center in a certain region as an example.

1. 引言

全球经济复苏和互联网飞速发展推动区域间信息和物资的频繁交流。我国物流业的发展起步相对较晚，但随着国民经济的腾飞，物流业的市场空间持续扩大，因此对物流中心绩效评价问题也就越突出。物流中心作为物资管理、物流分配和流通的据点，在整个物流系统中起着枢纽作用。

目前发达国家占全球物流行业的主导地位，拥有着相对成熟的物流系统和技术，而发展中国家处于相对落后的状态。随着社会经济的发展，大力发展物流行业在降低交易成本、提高经济效率、改善社会的投资环境、解决就业压力等方面都具有十分重要的意义，同时也能进一步促进国民经济的繁荣。物流中心绩效评价作为物流与供应链管理中的重要课题，对物流中心功能的实现和综合效益的提升发挥关键性作用。从以上分析可以看出研究物流中心绩效评价方法具有非常重要的理论意义和应用价值。

在一些经济发达国家从上世纪60年代就开始进行企业物流中心绩效评价，其中美国的鲍尔索克斯在1998年提出的物流绩效评价理论在国际上十分流行。鲍尔索克斯认为，物流绩效要从物流企业的内部和外部来进行评价，内部绩效评价着重于将当下的活动和过程与之前的作业和目标进行比较，外部绩效评价通常从客户感觉和最佳实施标准两个角度来界定。

物流中心集中了运输和存储等功能，绩效评价是物流中心效益的直观呈现，所以在物流中心绩效评价时应该考虑各项因素，并进行合理地系统分析，最后决定绩效最好的物流中心。

物流中心绩效评价问题的早期理论大多是由经济学家和通信学家提出的。在早期的研究中，作业成本在物流中心绩效评价具有重要作用。在物流系统分析与设计时，物流中心的配置常需得到模型化、数量化方法的支持，如动态规划、线性规划等运筹学的模型及方法。

在以往的物流中心绩效评价体系研究中，许多学者运用了平衡计分卡 [1]、层次分析法(AHP)和数据包络分析法(DEA)进行绩效评价研究 [2] - [7]。刘华采用平衡积分卡以新公共管理理论，公共选择理论和绩效管理理论为指导，将规范分析和实证分析相结合，综合公共管理学、统计学等多种学科知识对基层税务机关绩效进行评估。郑琰、许美贤两人针对港口物流效率构建指标体系，运用DEA模型对港口系统物流效率进行评价分析。在本文中，采用AHP/DEA结合的方法 [8] [9]，充分考虑决策者主观因素的重要性和客观因素数据的实际性，对物流中心绩效进行综合评价。

2. 研究方法

2.1. 基本数据包络分析法

数据包络分析法(Data Envelopment Analysis, DEA)，是数学、运筹学、管理科学和计算机科学的一个交叉研究领域，它是A. Charnes、W. W. Cooper和E. Rhodes为研究相对有效性，于1978年创建和命名的 [10] [11] [12] [13]。

在分析过程中，DEA将权重以变向量的形式体现，从最有利于被评价单元的角度自由地设定权重，因而可以得出最有利于决策单元的相对效率。由于DEA的优越性，才会吸引了越来越多的DEA理论与应用的研究者 [14] [15] [16]，在本文中适合采用DEA对物流中心绩效进行评价。

其最初提出的是CCR模型，它的规模报酬不变，随后将CCR模型中的综合技术效率(TE)细分为纯技术效率(PTE)和规模效率(SE)，修正为规模报酬可变的BCC模型 [17] [18] [19]。分解公式为：

$\text{TE}=\text{PTE}\times \text{SE}$, (1)

式中：TE是衡量决策单元(DMU)的资源利用是否充分、资源配置是否合理；PTE表示将投入转化为产出的技术水平；SE是衡量决策单元是否在合适的规模下生产。

设有n个决策单元，每个决策单元都有m个输入和s个输出，分别记第j个决策单元的输入和输出为

$X_j={\left(x_{1j},x_{2j},\cdots ,x_{mj}\right)}^{\text{T}},j=1,2,\cdots ,n$

$Y_j={\left(y_{1j},y_{2j},\cdots ,y_{sj}\right)}^{\text{T}},j=1,2,\cdots ,n$

其中 $x_{ij}>0$， $y_{rj}>0$ ( $i=1,2,\cdots ,m$， $r=1,2,\cdots ,s$ )分别表示第j个决策单元 ${\text{DMU}}_j$ 的第i种类型的输入量和第r种类型的输出量，它们可由观察到的样本数据中得到。

对第 $j_0$ ( $1\le j_0\le n$ )个决策单元进行效率评价，采用BCC模型得式(2)：

$\begin{array}{l}\min \theta -\epsilon \left({\displaystyle \underset{r=1}{\overset{s}{\sum }}{s}_r^{+}}+{\displaystyle \underset{i=1}{\overset{m}{\sum }}{s}_i^{+}}\right)\\ \text{s}\text{.t}.{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\lambda }_j{x}_{ij}}+s_i^{-}=\theta x_{ik},i=1,2,\cdots ,m\\ {\displaystyle \underset{j=1}{\overset{n}{\sum }}{\lambda }_j{y}_{rj}}-s_r^{+}=y_{rk},r=1,2,\cdots ,s\\ {\lambda }_j\ge 0,j=1,2,\cdots ,n\\ s_r^{+}\ge 0,s_i^{-}\ge 0,r=1,2,\cdots ,s,i=1,2,\cdots ,m\end{array}$ (2)

其中 $s^{+}=\left(s_1^{+},s_2^{+},\cdots ,s_s^{+}\right)$ 和 $s^{-}=\left(s_1^{-},s_2^{-},\cdots ,s_m^{-}\right)$ 分别为产出、投入对应的松弛变量， $\epsilon$ 为非阿基米德无穷小变量， $\lambda$ 为权重变量。当 $\theta =1$ 时，就表明该决策单元处于DEA有效。

2.2. 含偏好锥的数据包络分析模型

在DEA模型C²R中，m种输入指标和s种输出指标在评价决策单元的有效性时，所处的地位是等同的，即 $m+s$ 项指标重要性的权系数 $u^{\text{T}}$ 和 $v^{\text{T}}$ 之间没有任何约束。为了在DEA模型中反映出这些事实或要求(即决策者的偏好)，Charnes等人分别于1989年和1996年提出的被称为“锥比率”DEA模型(Cone ratio DEA model)，即C²WH模型 [20] [21] [22] [23]。

模型中带有体现决策者对输入和输出指标之间重要性的“偏好锥”和体现对决策单元侧重的“偏袒锥”，C²WH模型可以看作综合DEA模型中的一个特例，其在一定程度上能反映决策者的偏好。

设 $V=\left\{\omega |A\omega \ge 0\right\}\subset E_m^{+}$ 为闭凸锥，称为输入锥； $U=\left\{\mu |B\mu \ge 0\right\}\subset E_s^{+}$ 为闭凸锥，称为输出锥； $K=\left\{k|Rk\ge 0\right\}\subset E_n^{+}$ 为凸锥，称为偏袒锥，这里的A，B和R分别为 $m\times m$， $s\times s$ 和 $n\times n$ 方阵， $k^{\text{T}}=\left(k_1,k_2,\cdots ,k_n\right)$。C²WH模型可以写成如式(3)：

$\begin{array}{l}\max {\mu }^T{Y}_{j_0}\\ \left({\text{C}}^{\text{2}}\text{WH}\right)\text{s}\text{.t}\text{.}{\omega }^{\text{T}}{X}_j-{\mu }^{\text{T}}{Y}_j\in K\text{,}j=1,2,\cdots ,n\\ {\omega }^{\text{T}}{X}_{j_0}=1\\ \omega \in V,\mu \in U\end{array}$ (3)

若用 $V^{\ast }$， $U^{\ast }$ 和 $K^{\ast }$ 分别表示V，U和K的负极锥，即

$V^{\ast }=\left\{\omega |A\omega \le 0\right\}$， $U^{\ast }=\left\{\mu |B\mu \le 0\right\}$， $K^{\ast }=\left\{k|Rk\le 0\right\}$

那么将 $V^{\ast }$， $U^{\ast }$ 和 $K^{\ast }$ 分别代入C²WH模型的对偶规划模型，则有

$\begin{array}{l}\min \theta \\ \left({\text{D}}_{{\text{C}}^{\text{2}}\text{WH}}\right)\text{s}\text{.t}\text{.}{\lambda }^{\text{T}}{X}_j-\theta X_{j_0}\in V^{\ast }\text{,}j=1,2,\cdots ,n\\ -{\lambda }^{\text{T}}{Y}_j+Y_{j_0}\in U^{\ast }\text{,}j=1,2,\cdots ,n\\ \lambda \ge -K^{\ast }\end{array}$ (4)

2.3. 层次分析法

本文中案例计算涉及到决策者的主观因素无法用确切的数据进行表示，因此引入层次分析法对决策者的主观因素进行权重排序。接下来对层次分析法的基本理论进行简单介绍。

层次分析法(Analytical Hierarchy Process, AHP)是美国匹兹堡大学教授撒泰(A. L. Saaty)提出的一种系统分析方法。它采用综合定性与定量相结合的分析过程，对多因素复杂系统(特别需要定性描述的系统)进行分析，因此被认定为是决策科学化的一大进步。通常采用AHP解决实际问题的步骤是，首先，把问题分层次系列化，将问题分解为不同的组成因素，按照因素之间的相互影响程度和隶属关系将其分层聚类组合，形成一个分阶的、有序的层次结构模型；然后，依据人们对客观方面的判断使用定量方法来表示模型中每一层次因素的相对重要性，再利用方法确定各层次因素相对重要性权值以及次序；最后，通过综合计算各层因素的权值来得到最低层相对于最高层的组合权值，该组合权值可作为选择方案数据处理的依据。

运用AHP解决实际问题，首先要明确分析决策的问题，并将其的因素条理化、层次化理出递阶层次结构。

物流中心绩效评价因素都是遵循适应性原则、协调性原则、经济性原则以及战略性原则。本文层次结构见图1。

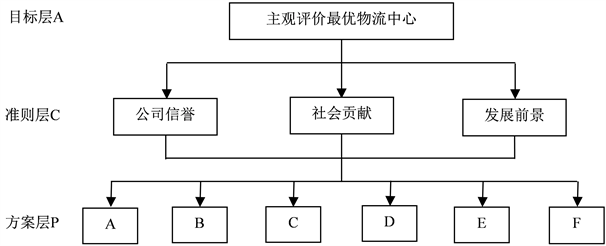
Figure 1. Hierarchical structure model of evaluating logistics company performance

图1. 评价物流公司绩效的层次结构模型

图1中目标层A表示应用AHP所要达到的目标；准则层C表示实现预定目标所涉及的中间环节，包括策略层、约束层、准则层等；方案层P表示解决目标问题的措施或政策。

通常情况下，系统分析都必须以信息为基础。AHP的信息基础主要是人们对每层中各个因素的相对重要性给出的数值判断，以矩阵形式写出，即为判断矩阵，构造判断矩阵是AHP工作的开始阶段，也是关键的一步。层次单排序是根据判断矩阵计算出的相对于上一层某因素的本层次中与之有关系的因素的重要性次序的权值。该排序可以通过计算判断矩阵的特征根和特征向量， ${\lambda }_{\max }$ 为最大特征值； $\omega$ 为对应于 ${\lambda }_{\max }$ 的正规化特征向量； $\omega$ 的分量 ${\omega }_i$ 为相应元素的单排序权值。

3. 实证分析

本论文题目要求对物流中心进行绩效评价分析研究，选择出绩效最优的物流中心，因此在本章中以多个物流中心为例，结合DEA和AHP两种方法，对案例进行深入研究。

3.1. 投入、产出指标体系构建

基于数据包络分析法的物流中心绩效评价，本节选取某地区六家物流中心A、B、C、D、E和F为例，输入元素选取作业成本和人员调度率，输出元素选取利润、服务准确率和服务及时率，构建客观实际数据、带有输出偏好的数据以及对评价对象赋予权重的数据的数学模型对物流中心进行综合分析。方案层输入输出因素见表1。

Table 1. Input and output data table of logistics center

表1. 物流中心输入输出数据表

3.2. 建立基本的绩效评价模型

基本的绩效评价模型是根据物流中心表1的输入、输出数据构建的，这是一个对数据不做任何处理的模型，将运用具有非阿基米德无穷小的C²R模型，对应于DMU(A)，代入公式(2)，得对应的 $\epsilon$ 和 $S^{+},S^{-}$ 值：

$\{\begin{array}{l}\min \left[\theta -\epsilon \left(S_1^{-}+S_2^{-}+S_3^{+}+S_4^{+}+S_5^{+}\right)\right]\\ \begin{array}{cc}\text{s}\text{.t}\text{.}& 65{\lambda }_1+68{\lambda }_2+63{\lambda }_3+56{\lambda }_4+70{\lambda }_5+68{\lambda }_6+S_1^{-}=65\theta \end{array}\\ \begin{array}{cc}& 0.155{\lambda }_1+0.179{\lambda }_2+0.144{\lambda }_3+0.170{\lambda }_4+0.183{\lambda }_5+0.169{\lambda }_6+S_2^{-}=0.155\theta \end{array}\\ \begin{array}{cc}& 15{\lambda }_1+18{\lambda }_2+13{\lambda }_3+9{\lambda }_4+16{\lambda }_5+19{\lambda }_6-S_3^{+}=15\end{array}\\ \begin{array}{cc}& 0.985{\lambda }_1+0.978{\lambda }_2+0.895{\lambda }_3+0.926{\lambda }_4+0.963{\lambda }_5+0.992{\lambda }_6-S_4^{+}=1\end{array}\\ \begin{array}{cc}& 0.967{\lambda }_1+0.983{\lambda }_2+0.869{\lambda }_3+0.910{\lambda }_4+0.865{\lambda }_5+0.987{\lambda }_6-S_5^{+}=0.967\end{array}\\ \begin{array}{cccccc}{\lambda }_1\ge 0& {\lambda }_2\ge 0& {\lambda }_3\ge 0& {\lambda }_4\ge 0& {\lambda }_5\ge 0& {\lambda }_6\ge 0\end{array}\\ \begin{array}{ccccc}{S}_1\ge 0& S_2\ge 0& S_3\ge 0& S_4\ge 0& S_5\ge 0\end{array}\end{array}$

利用LINGO软件计算可得结果：

$\{\begin{array}{l}\theta =1\\ S_1^{-}=S_2^{-}=S_3^{+}=S_4^{+}=S_5^{+}=1\\ \begin{array}{cc}{\lambda }_1=1& {\lambda }_2={\lambda }_3={\lambda }_4={\lambda }_5={\lambda }_6=0\end{array}\end{array}$

由DMU(A)计算结果可得为DEA有效。

类似于DMU(A)计算过程，可得其余决策单元的 $\theta$ 、 $S^{\text{+}}$ 、 $S^{-}$ 和 ${\lambda }_i$ 结果，具体数据见表2。

Table 2. Calculation results of DMU effective values

表2. DMU有效值计算结果

由表2中数据结果可知，决策单元A、D和F结果为DEA有效，在此结果上我们可以认定A、D和F的三个物流中心绩效相对比较优秀，因此在选择物流中心时尽量考虑从这三个中选择，这样有利于选择最优的物流中心，而相对于这三个物流中心，其余的B、C和E三个就有不足之处，物流中心B相对于其余两个方案是最接近有效值1，它在人员调度率和服务准确率两项中具有改动的空间物流中心B。

3.3. 含输出偏好锥的数学模型

在物流中心绩效评价实际问题，实际的数据往往不会直接运用于模型计算，通常会存在决策者的偏好问题，如决策者比较注重输入或输出元素某个单元的数据，因此在输入输出单元中存在着相对重要性比例。在这一节中，将采用含输出偏好的模型为例，结合表1中的数据，并对数据进行处理。

通过对决策者偏好的进行分析，可得出对应的判断矩阵，见表3。

Table 3. The judgment matrix with output preference

表3. 含输出偏好的判断矩阵

依据表3计算，并构造矩阵 $A=A_0-{\lambda }_{\max }{E}_0$，即

$A=\left[\begin{array}{ccc}-2& 4/3& 4/3\\ 3/4& -2& 1\\ 3/4& 1& -2\end{array}\right]$.

构造闭凸锥 $Aw\ge 0$，即

$\left[\begin{array}{ccc}-2& 4/3& 4/3\\ 3/4& -2& 1\\ 3/4& 1& -2\end{array}\right]\left[\begin{array}{l}{w}_1\\ w_2\\ w_3\end{array}\right]\ge 0$,

其中 $w={\left(w_1,w_2,w_3\right)}^{\text{T}}\ge 0$。

对应于DMU(A)和带有偏好锥的模型，可以得出计算公式：

$\begin{array}{l}\max h=65v_{\text{1}}+\text{0}\text{.155}{v}_{\text{2}}\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}15w_1+0.985w_2+0.967w_3=1\\ 65v_1+0.155v_2-\left(15w_1+0.985w_2+0.967w_3\right)\le 0\\ 68v_1+0.179v_2-\left(18w_1+0.978w_2+0.983w_3\right)\le 0\\ 63v_1+0.144v_2-\left(13w_1+0.895w_2+0.869w_3\right)\le 0\\ 56v_1+0.170v_2-\left(9w_1+0.926w_2+0.910w_3\right)\le 0\\ 70v_1+0.183v_2-\left(16w_1+0.963w_2+0.865w_3\right)\le 0\\ 68v_1+0.169v_2-\left(19w_1+0.992w_2+0.987w_3\right)\le 0\\ Aw\ge 0\\ w={\left(w_1,w_2,w_3\right)}^{\text{T}}\ge 0,u={\left(u_1,u_2\right)}^{\text{T}}\ge 0\end{array}\end{array}$

在此模型中可直接得出物流中心决策单元的有效值，并没有附带偏差值，由此可得DMU(A)的有效值 $h=0.7316$。类似DMU(A)的计算方法，结合输出单元权重向量可计算出其余DMU的有效值，其结果见表4。

Table 4. Results of valid values with output preference cones

表4. 含输出偏好锥的有效值结果

由表4中数据结果可知，只有决策单元D结果为1，是DEA有效的，在此结果上我们可以认定只有D物流中心绩效比较优秀，因此在选择物流中心时尽量考虑选择D，而相对于这个方案，其余的5个方案就有不足之处。

3.4. 基于AHP/DEA的数学模型

综合考虑3.2和3.3中的两个模型和各个模型的优缺点后，结合两种模型，构建出基于AHP/DEA的数学模型。该模型可以考虑实际数据的准确性和决策的偏好，是物流中心绩效评价的优化模型。

根据图1中的准则层，我们分别从公司信誉、社会贡献和发展前景三个方面综合决策物流中心。通过决策者对上述三个方面的分析，可以形成准则层的判断矩阵见表5。

Table 5. Criteria layer judgment matrix

表5. 准则层判断矩阵

依据三个因素，以方案层决策单元为基础构建判断矩阵，并对各个判断矩阵进行一致性检验，最终计算出最大特征值和权重向量。以公司信誉为元素构建判断矩阵，见表6。

Table 6. Judgment matrix of company reputation

表6. 公司信誉的判断矩阵

由公司信誉的判断矩阵计算，同理可以得出社会贡献和发展前景的计算结果。由以上准则层的权重向量和各个因素矩阵的权重向量，最终可得出综合权重排名，见表7。

Table 7. Comprehensive weight ranking of decision making units

表7. 决策单元综合权重排名

由表7可得出各个物流中心点的总权重，该权重是决策者期望输出，因此，可以将总权重数据添加至输出元素模块，可得出物流中心非定性量化输出量，以DMU(A)为例，得出计算模型：

$\{\begin{array}{l}\max V=15u_1+0.985u_2+0.967u_3+0.0760u_4\\ \begin{array}{cc}\text{s}\text{.t}\text{.}& 65v_1+0.155v_2=1\end{array}\\ 15u_1+0.985u_2+0.967u_3+0.0760u_4-65v_1-0.155v_2\le 0\\ 18u_1+0.978u_2+0.983u_3+0.0918u_4-68v_1-0.179v_2\le 0\\ 13u_1+0.895u_2+0.869u_3+0.0699u_4-63v_1-0.144v_2\le 0\\ 9u_1+0.926u_2+0.910u_3+0.1429u_4-56v_1-0.170v_2\le 0\\ 16u_1+0.963u_2+0.865u_3+0.2485u_4-70v_1-0.183v_2\le 0\\ 19u_1+0.992u_2+0.987u_3+0.3709u_4-68v_1-0.169v_2\le 0\\ \begin{array}{cc}-v_1\le -0.000001& -u_1\le -0.000001\end{array}\\ \begin{array}{cc}{v}_2-v_1\le 0& u_2-u_1\le 0\end{array}\\ \begin{array}{cc}{u}_3-u_2\le 0& u_4-u_3\le 0\end{array}\\ \begin{array}{cc}-v_2\le -0.000001& -u_4\le -0.000001\end{array}\end{array}$

由LINGO计算软件可得结果：

$\begin{array}{cccc}{V}^{\ast }=0.8454& v^{\ast }=\left(\begin{array}{cc}0.0153& 0\end{array}\right)& u_1=u_2=u_3=0.0499& u_4=0\end{array}$

由DMU(A)的计算过程，可以类似的计算出其余决策单元的有效值以及偏差值，数据结果见表8。

Table 8. Calculation results based on AHP/DEA model

表8. 基于AHP/DEA模型计算结果

由表8中数据结果可知，综合AHP/DEA模型的数据有效值，可以得出只有决策单元F的DEA有效值为1，即为最优物流中心。AHP/DEA综合模型既考虑了客观实际数据，又能反应出决策的偏好，得出有效值评价，相对于3.2和3.3中的模型更具有参考性。

4. 结论

虽然目前国内外学术界针对物流中心效率评价的研究逐渐被重视，但大多数只是从客观的因素上进行理论分析，缺乏通过一套有效的、科学的、准确的综合评价方法建立起来的评价标准。考虑决策者主观因素的研究较少，仍需进一步研究。基于此，本文首先采用数据分析方法对物流中心绩效进行评价。其次，利用层次分析法对各指标进行赋权后进行绩效评价。最后，将层次分析法和数据包络分析相结合对物流中心效率进行评价，基于AHP/DEA的数学模型利用AHP构建反映决策人偏好的约束锥，其与客观数据一起应用于DEA模型评价中，使评选过程透明化，减少人为因素影响，更加公正地选择出最优的物流中心。

由于本人水平有限，本论文还存在一些缺陷，需要加以改进，主要体现在：文中涉及的影响因素只是实际问题中的一部分，评价结果可能不精确。由于数据包络分析法的发展空间很大，在应用方面的研究还不够，在今后的物流绩效评价中，可以采用更为系统的影响因素和各因素权值，来完善数据包络分析法在物流中心绩效评价中的应用。