RN 上一类p-Kirchhoff方程解的存在性研究
Study on Existence of Solutions for a p-Kirchhoff Elliptic Equation on RN
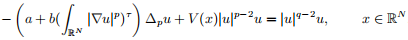
摘要: 本文研究如下一类p-Kirchhoff椭圆方程, (1) 非平凡弱解的存在性。其中 a, b, τ > 0, 1 < p < N, p < q < p(τ + 1) < p∗ 。基于变分原理，我们证得方程(1)至少存在一个非平凡解。本文的主要困难在千论证近似解序列的有界性和收敛性。
Abstract: In this paper, we study the existence of solutions for the following p-Kirchhoff elliptic equation , (1) with a, b, τ > 0, 1 < p < N, p < q < p(τ + 1) < p∗. By the variational methods, we prove that problem (1) admits at least one nontrivial solution. The main difficulty is to get a bounded (PS) sequence and extract a strong convergent subsequence from it.
文章引用：刘立华. RN 上一类p-Kirchhoff方程解的存在性研究[J]. 应用数学进展, 2021, 10(12): 4262-4271. https://doi.org/10.12677/AAM.2021.1012453

参考文献

[1] Kirchhoff, G. (1883) Vorlesungen u¨ber Mechanik. Teubner, Leipzig.
[2] Corrˆea, F.J.S.A. and Figueiredo, G.M. (2006) On a Elliptic Equation of p-Kirchhoff Type via Variational Methods. Bulletin of the Australian Mathematical Society, 74, 263-277.
https://doi.org/10.1017/S000497270003570X
[3] Corrˆea, F.J.S.A. and Figueiredo, G.M. (2009) On a p-Kirchhoff Equation via Krasnoselskii’s Genus. Applied Mathematics Letters, 22, 819-822.
https://doi.org/10.1016/j.aml.2008.06.042
[4] Liu, D. and Zhao, P. (2012) Multiple Nontrivial Solutions to a p-Kirchhoff Equation. Nonlinear Analysis, 75, 5032-5038.
https://doi.org/10.1016/j.na.2012.04.018
[5] Li, G. and Ye, H. (2014) Existence of Positive Ground State Solutions for the Nonlinear Kirchhoff Type Equations in R3. Journal of Differential Equations, 257, 566-600.
https://doi.org/10.1016/j.jde.2014.04.011
[6] Ikoma, N. (2015) Existence of Ground State Solutions to the Nonlinear Kirchhoff Type Equa- tions with Potentials. Discrete and Continuous Dynamical Systems, 35, 943-966.
https://doi.org/10.3934/dcds.2015.35.943
[7] Li, Y.H., Li, F.Y. and Shi, J.P. (2012) Existence of a Positive Solution to Kirchhoff Type Problems without Compactness Conditions. Journal of Differential Equations, 253, 2285-2294.
https://doi.org/10.1016/j.jde.2012.05.017
[8] Jeanjean, L. (1999) On the Existence of Bounded Palais-Smale Sequence and Applications to a Landesman-Lazer-Type Set on RN . Proceedings of the Royal Society of Edinburgh Section A, 129, 787-809.
https://doi.org/10.1017/S0308210500013147
[9] Willem, M. (1996) Minimax Theorem. Birkh¨auser, Inc., Boston, MA.
[10] Chen, C.S. (2016) Infinitely Many Solutions to a Class of Quasilinear Schr¨odinger System in RN . Applied Mathematics Letters, 52, 176-182.
https://doi.org/10.1016/j.aml.2015.09.007
[11] Kuzin, I. and Pohozaev, S. (1997) Entire Solutions of Semilinear Elliptic Equations. In: Brezis, H., et al., Eds., Progress in Nonlinear Differential Equations and Their Applications, Vol. 33, Birkh¨auser, Boston, MA.

为你推荐