1. 引言
随着深空测控通信及射电天文观测的发展需求,射电望远镜正朝着大口径、高频段、高指向与跟踪精度方向发展。指向精度作为射电望远镜重要的性能指标,直接影响着射电望远镜观测目标时的信号接收能力以及观测效率。因此射电望远镜指向误差测量以及其精度的提升一直受到广泛的关注研究 [1] [2]。
大型射电望远镜通常结构复杂,影响其指向精度的因素很多并且性质复杂。有的影响因素有清晰的分布规律,有的影响因素具有随机变化无明显分布规律的特点。其中方位轴倾斜 [3],重力变形误差 [4],轨道沉降 [5] [6]、大气折射误差 [7] [8]、风载荷 [9] [10]、温差 [11] 造成的形变以及伺服传动等都是造成指向误差的重要因素。针对射电望远镜校正问题,国内外在射电望远镜指向误差源分析与精度提升方面有很多研究工作。通常提高望远镜指向精度的方式有两种。第一种是硬件校准 [12],通过提高硬件设备的加工与装配精度来提高望远镜的指向精度。硬件校准一般在天线建造安装时通过工程方法有效完成,使得天线具备一定指向精度,但是受限于工程工艺以及造价成本,有些误差仍无法通过硬件校准完全消除;第二种是软件标校 [13] [14],通过分析所能识别的误差源,建立指向误差修正模型,并用伺服系统对指向误差进行模型实时修正补偿来提高望远镜的指向精度。主要的误差模型包括:基本参数模型,球谐函数模型以及神经网络模型等。其中基本参数模型,参数物理含义明显,模型修正稳定,因此广泛应用于各类天线指向修正。由于不同射电望远镜天线结构各异以及在不同的实验环境下,其指向误差修正模型在基本参数修正模型的基础上多少会有所差异,通常会在基本参数的基础上增加一些经验项。比如用于大型轮轨式射电望远镜的方位轴非线性倾斜偏差的指向修正方法 [5] 以及基于广义延拓差值的射电望远镜指向误差修正模型 [13] 等。
基于观测任务要求,本文利用射电源对射电望远镜天线各方向指向进行了测量。针对原始误差提取算法的适应性不好的特点,本文提出了一种基于拟合优度检验的有效指向误差提取算法,随后分析了修正模型,并针对最小二乘法拟合求解模型系数缺乏容错能力的特点,提出了一种基于残差统计检验的容错修正方法,提高了模型参数估计的精度。
2. 射电望远镜指向误差测量及提取
2.1. 指向数据采集
射电源具有稳定、位置精确、有一定带宽等特点,因此选择射电源作为射电望远镜指向误差测量的观测目标源。
由天线功率方向图可知,若望远镜指向精确对准射电源时,天线接收的功率信号最强。当望远镜指向偏离目标射电源时,天线接收功率信号强度会随之降低。根据上述特性,可首先引导天线指向目标射电源,然后引导天线偏开射电源,分别在方位与俯仰对射电源进行角度偏置扫描,在扫描过程中同时记录当前射电源理论位置、天线实际位置以及功率计采集的信号功率。在引导天线对一个射电源进行方位与俯仰扫描之后,会得到功率信号随方位与俯仰值变化的一条曲线。此扫描过程中,天线在天空中扫描到的位置形如一个“十”字,因此称之为十字扫描法(如图1所示,先方位扫描后俯仰扫描)。

Figure 1. Diagram of cross scanning method
图1. 十字扫描法示意图
射电望远镜在不同方向的指向误差,需要对不同方位和俯仰上的射电源进行十字扫描测量。其中可用于天线指向误差测量理想的射电源应具有以下条件 [15] [16]:
深空测控网的主要技术特点如下:
1) 在天球上的位置精确已知,并在天球上有较均匀的分布和覆盖较大的分布区域;
2) 对被测射电望远镜的频段内,有足够的信噪比,即射电源在所测频段内具有较大流量密度;
3) 对被射电望远镜天线波束宽度而言,射电源角径应相对较小,即可被视为点源目标;
4) 附近没有其它较强的射电源或银河背景辐射。
为了提高测量效率,射电望远镜观测系统通常采用自动化方式运行。首先设置好运行约束条件如开始时间、结束时间、角度上下限、偏置宽度、扫描周期、选择的射电源等。系统根据约束条件完成射电源的轨道预报并规划自动测量最优跟踪计划,随后程序控制天线按照规划的测量计划对不同方向的射电源轮流进行十字扫描,同时记录各项参数形成指向测量数据。
2.2. 指向误差提取
若射电望远镜的指向没有误差,则其在对射电源进行扫描过程中,天线相对于射电源的角度偏置为零时,输出的功率信号最大。反之当射电望远镜存在指向误差时,功率曲线的峰值对应的天线实际指向与射电源理论指向存在一定的偏差,表征了射电望远镜在该位置的指向误差。
由于十字扫描所得功率结果为离散形式,且通常所收功率信号存在噪声干扰,所以数据的最大值点并不一定为功率变化曲线的峰值点。天线扫描射电源得到的功率变化曲线实际上是望远镜的波束响应函数与射电源角径方向能量分布卷积。假定望远镜的主瓣波束宽度附近响应近似为高斯函数,射电源在角径方向上的能量符合高斯分布。根据高斯分布的性质可知,功率变化曲线波形近似符合高斯函数。因此实际工作任务中采用如下高斯函数拟合功率变化曲线:
(1)
其中x为观测采样点序号,a、b、c为待拟合的高斯参数。为了提高曲线拟合的准确度,首先对原始扫描数据进行阈值分割,由阈值确定候选采样数据,并根据候选数据的连续性判断候选的有效性,最后将有效采样数据作为拟合的数据(以下称“提取算法1”)。实际使用中采用上述高斯函数方法实现拟合的过程中发现结果有时并不理想。如图2(a)所示,当扫描所得功率曲线受噪声干扰影响较小时,所得结果能够满足指向误差提取要求;当扫描所得功率曲线受噪声干扰严重时,应剔除该段扫描数据(如图2(b)所示)。综上分析本文采用一种更加鲁棒的误差提取算法(以下称“提取算法2”)进行了天线指向误差提取。考虑功率信号存在底噪,功率的分布并不能满足(1)式所表示的单纯的高斯函数,采用如下高斯函数:
(2)
同样对原始扫描数据利用阈值进行分割。根据式(2)首先功率变化数据对参数进行初值估计{a0 b0 c0
d0}。然后选择坐标为
所在的区间数据作为有效采样数据进行数据拟合。
用R2统计量度量模型对数据变化的符合程度
(3)
其中
,
。需要指出的是R2统计量来源于线性回归,一般而言对
于非线性回归,当模型选择正确,回归拟合好时,R2统计量能够如实反映回归拟合效果 [17]。该统计量越接近1,则模型的拟合优度越高(如图2(c)、图2(d)所示,以下称“提取算法2”)。
 (a) 有效提取
(a) 有效提取  (b) 无效提取
(b) 无效提取  (c) R2 = 0.9985
(c) R2 = 0.9985  (d) R2 = 0.6443
(d) R2 = 0.6443
Figure 2. Diagram of pointing error extraction cross: (a) (b) “method 1”; (c) (d) “method 2”
图2. 拟合指向误差提取示意图:(a)、(b) “提取算法1”;(c)、(d) “提取算法2”
3. 指向误差源分解与建模
射电望远镜的指向误差由很多因素造成。按误差来源可以静态误差源和动态误差源两种。静态误差主要指结构件制造以及安装调整过程中产生的误差。动态误差主要指结构动态变形引起的误差以及系统运行过程中产生的动态误差。按误差性质,上述各项误差皆可分为系统误差和随机误差,其中随机误差可通过测量数据的平滑处理,使其影响减小;系统误差可通过硬件校准与软件校准方法来减小其影响。
对于大口径射电望远镜,硬件校准通常包括天线的轴系校准、馈源最佳位置的调整、轴角位置指示器校准、电轴校准和温度变形补偿等方面,硬件校准一般只在安装调试过程中通过工程方法进行校准。受机械加工和调整精度的限制,天线轴系、编码器等安装总存有微小的系统误差,并且在后续天线运行的过程中以后很难再进行硬件校准修正。因此通常还需对指向误差进行分析和观测,建立指向误差修正模型,通过软件校准的方法对天线进行进一步指向误差补偿才能满足实际观测精度要求。
3.1. 主要误差源概述
射电望远镜的指向误差源主要包括:天线电轴和机械轴不重合,俯仰轴与方位轴不正交,天线的方位轴偏离天顶、方位和俯仰编码器的零位偏差、天线重力变形误差以及大气折射误差等。根据上述主要误差源可建立射电望远镜指向误差线性分解模型如式(4)所示 [13]:
(4)
式(4)中,
为方位差,
为俯仰差,A为方位值,E为俯仰值,εA与εE分别为方位俯仰的随机误差项,C1~C8为模型参数,其中C1为方位编码器零点误差,C2为俯仰编码器零点误差,C3为方位轴倾斜误差,C4为方位轴倾斜方向误差,C5为俯仰轴与方位轴不正交误差,C6为电轴与俯仰轴不正交误差,C7为重力变形误差,C8为大气校正模型残差 [13]。为了分析方便,式(4)可统一抽象地表示为矩阵形式如下
(5)
式中:
为观测向量;
为
阶设计矩阵;
为待估计的模型参数向量。
式(5)的参数估计问题可用最小二乘(LS: the least squared)估计求解:
(6)
3.2. 观测值容错修正模型
尽管2.2节中指向误差提取方法能够有效的提取指向误差,但也仍不能完全排除个别离群值点。由于LS估计缺乏容错能力,若观测序列数据中存在离群值点则会导致LS参数估计效果变差,因此需要对误差观测序列进行核验,对观测序列进行合理的离群值判别与处理,提高参数估计的精度。
在式(6)基础上,可得到参数估计残差如下:
(7)
其中I为单位矩阵,
为帽子矩阵。
定义剔除样本i残差ei:用剔除第i个观测值的其余观测值进行最小二乘参数估计
,计算出第i个观测值的剔除拟合值
,则
同理剔除样本 误差项方差
的无偏估计如下:
(8)
构造统计量Ti如下:
(9)
其中hii为H中位于第i行第i列的元素。可以证明Ti服从t分布,即
。
在给定显著性水平α情况下,t检验方法如下:
(10)
若上式成立,即可判断第i个观测值为离群值点应予以剔除,否则可认为有效观测值。
3.3. 误差模型的方程显著性检验
为了分析和检验指向误差的主要部分是否已经包含在所采用的模型中,需要对所采用模型的拟合效果进行判断。对此提出假设计算进行方程显著性检验,做出拒绝H0或H1的判断结论:
(11)
定义最小二乘参数估计的残差平方和为SSE,回归平方和为SSR。构造统计量F如下:
(12)
可以证明,若
成立,则统计量F服从自由度为
的F分布。在给
定显著性水平α情况下,F检验方法如下:
(13)
若上式成立,则拒绝原假设H0,即模型的线性关系显著成立,模型通过方程显著性检验,误差模型能够满足误差修正效果;反之模型未通过方程显著性检验,误差模型不能够满足误差修正效果。
3.4. 误差模型的分量显著性检验
模型方程显著性检验只能检验模型方程是否遗漏了主要误差项,不能直接用于判断是否有不必要的误差分量被引入误差模型中,也无法判定哪些误差分量已经被提前修正。为此构造误差模型的分量的显著性检验的算法,同时用以评价模型分量的差异程度。
对此提出假设进行计算判断,做出拒绝H0或H1的结论:
(14)
对于参数估计
,若
,则
,于是有
,其中cjj为矩阵
中的第j行第j列的元素。
构造统计量tj如下
(15)
可以证明,若
成立,则统计量tj服从自由度为(n-p-1)的t分布。在给定显著性水平α情况下,t检验方法如下:
(16)
若上式成立,则拒绝原假设H0,即认为模型分量βj显著不为零,即表明βj对应误差项分量对总误差的贡献是显著的,反之对应误差项分量对总误差的贡献是不显著的。
4. 实验结果与分析
4.1. 实测数据结果
为了评估该算法的性能,选择3C144,3C274,3C123,3C461等共12个强射电源作为目标源进行了射电望远镜的指向数据测量采集,得到360个测量数据点,其中方位俯仰各180个,指向误差测量点在方位和俯仰上的分布如图3所示。
为了解天线指向误差的具体情况,分别采用指向误差“提取算法1”、“提取算法2”提取各测量点的指向误差。根据指向误差“提取算法1”可以筛选出135个方位有效误差数据与174个俯仰有效误差数据。根据指向误差“提取算法2”可以筛选出143个方位有效误差数据,176个俯仰有效误差数据。图4显示了“提取算法1”提取的方位与俯仰指向误差随方位A和俯仰E的变化。
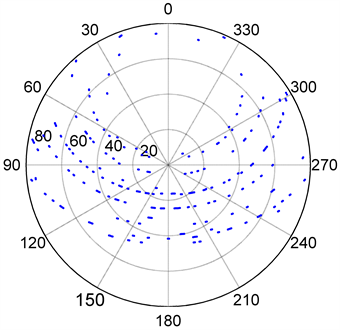
Figure 3. Distribution of the measured pointing error in horizontal coordinates
图3. 指向误差测量点在地平坐标下的分布
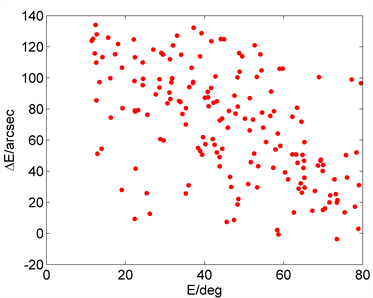
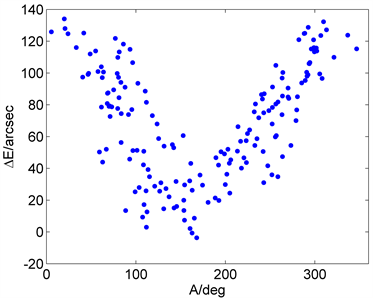
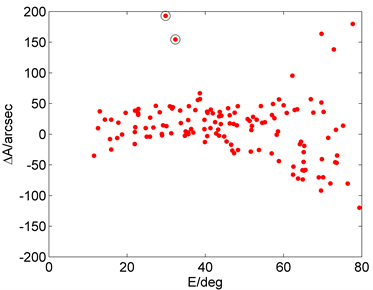
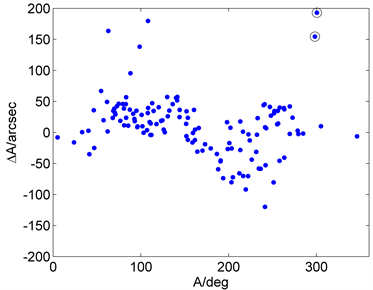
Figure 4. The varies of extracted azimuth error ΔA and elevation error ΔE with azimuth A and elevation E
图4. 提取的有效误差数据方位误差ΔA和俯仰误差ΔE随方位A和俯仰E变化
从图4可以看出射电望远镜的指向误差随方位和俯仰有明显的变化趋势。两种算法所提取的指向误差分布基本一致。对有效误差提取数据进行如下统计计算得到方位、俯仰指向误差均方根。
(17)
而射电望远镜指向误差δ则为:
(18)
“提取算法1”得得到的天线方位指向误差均方根δA = 28.69″,俯仰指向误差均方根δE = 78.45″,指向总误差δ = 83.53″。“提取算法2”得到的天线方位指向误差均方根δA = 21.64″,俯仰指向误差均方根δE = 78.22″,指向总误差δ = 81.16″。其中“提取算法1”与“提取算法2”主要差别在于方位指向误差均方根相差较大,这主要是由于“提取算法1”引入了两个明显的离群点所致(如图4“o”所标注)。此外可知若不对射电望远镜的指向进行误差修正,则其指向精度不能满足实际观测要求。下面将得到的初始误差数据分别利用式(4)的指向模型进行模型误差修正。
4.2. 模型误差修正结果分析
将3.1节得到的指向误差数据利用式(4)的模型进行拟合,得到了模型修正后方位与俯仰指向残差分布如图5所示。
由图5结果可以看出经模型修正后可以明显地改进天线的指向精度。其中模型修正后“提取算法1”得到的天线方位指向残差均方根δA = 26.55″,俯仰指向残差均方根δE = 20.36″,指向总残差δ = 33.46″。“提取算法2”得到的天线方位指向残差均方根δA = 18.88″,俯仰指向残差均方根δE = 18.91″,指向总残差均方根δ = 26.72″。“提取算法1”受限于若干离群点的影响,其模型修正精度不如“提取算法2”。计算指向误差观测序列的统计量Ti得到其分布如图6所示。
 (a) “提取算法1”
(a) “提取算法1”  (b) “提取算法2”
(b) “提取算法2”
Figure 5. The varies of calibrated azimuth error eA and elevation error eE with azimuth A and elevation E
图5. 指向误差模型修正后的方位残差eA和俯仰残差eE随方位A和俯仰E变化
 (a) “提取算法1”
(a) “提取算法1”  (b) “提取算法2”
(b) “提取算法2”
Figure 6. The varies of Statistics Ti from the measured error with azimuth A and elevation E
图6. 误差观测序列的统计量Ti随方位A和俯仰E变化
从图6可以看出“提取算法1”的统计量Ti在大部分位于−3至3之间,但是A方位的统计量Ti有明显的若干离群值存在,存在两个点的Ti大于3,而“提取算法2”的统计量Ti不存在明显的离群值,可知“提取算法2”提取误差的鲁棒性优于“提取算法1”。在给定显著性水平α = 0.01情况下,使用t检验方法剔除离群值(其中一个离群值为图2(b)所示的提取结果),重新进行模型参数估计,得到了模型容错修正指向误差的残差分布如图7所示。
 (a) “提取算法1”
(a) “提取算法1”  (b) “提取算法2”
(b) “提取算法2”
Figure 7. The varies of calibrated azimuth error eA and elevation error eE with azimuth A and elevation E
图7. 指向误差模型修正后的方位残差eA和俯仰残差eE随方位A和俯仰E变化
对比图5(a)与图7(a)的结果可以看出经过t检验离群值处理后的模型容错修正可以进一步改进天线的修正后的残差分布,从而使得图7(a)的结果与图7(b)指向精度结果相当。模型修正后“提取算法1”得到的天线方位指向残差均方根δA = 19.69″,俯仰指向残差均方根δE = 19.81″,指向总残差均方根δ = 27.93″。“提取算法2”得到的天线方位指向残差均方根δA = 18.8″,俯仰指向残差均方根δE = 18.52″,指向总残差均方根δ = 26.39″。综上图7以及数据结果可知经过修正后可以明显的改进天线的指向精度。
4.3. 模型参数显著性检验结果分析
为了检验所建立指向误差模型是否包含主要误差项以及核验误差模型分量是否必要或已被提前修正,计算图5的模型拟合优度统计量和模型系数显著性检验统计量结果如表1所示(表中的0表示其统计量P值小于10−4)。由表1可以得出有优于99.9%概率确信,误差修正模型吻合效果很好。

Table 1. The hypothesis test of the adopted model
表1. 模型的检验统计量
由表1中的模型系数统计量的P值可知,模型分量参数β1,β5,β6的P值显著不为零,则对应误差项分量对总误差的贡献是不显著的,这主要是由于在进行指向测量过程中为了天线更快的指向所测目标进行扫描,对天线位置的参数预修正。因此上述模型分量贡献不显著则标明预修正分量已满足修正要求。
5. 结论
本文基于观测任务要求筛选了射电望远镜适宜观测的射电源,利用目标射电源对天线各方向的指向误差进行了测量与提取。本文提出并分析了一种基于残差统计量检验的容错修正模型方法,能够有效地对误差观测序列进行离群值检验,提高了模型参数估计的精度。基于统计假设检验理论,利用模型拟合的F检验以及模型分量的t检验方法对引入的指向误差模型进行了显著性检验。基于观测实验验证表明:有效的指向误差与离群值的提取能够提高模型误差修正的精度,本次观测数据中可以从33.46″改进至26.39″。显著性检验方法可用于检测误差模型以及模型分量的有效性。在下一步工作中,为了更加精确地提高指向误差的精度,将进一步考虑温度、湿度、风载等其他因素,并分析显著性检验方法进行模型分量优选准则,建立相应的指向误差修正模型。
致谢
本项目受到“基于GEO卫星和月基平台的超远程频率传递与比对技术(ZFS19001D-ZTYJ02)”课题资助支持开展工作。