1. 引言
在我国南方地区的重要港口中,广州港的吞吐量一直位于业内前列。作为港内重要的装卸、搬运和堆放设备,轨道式集装箱门式起重机(简称:轨道吊)的作业量日益增多。随之而来的是,轨道吊小车机构车轮的运行时间也急剧增加,因此车轮的病害问题也引起了国内外学者的广泛关注 [1]。传感器作为工业的“神经触角”之一,是获取车轮动力学行为最直接的数据来源。而通过加速度传感器,可以感知车轮的振动加速度,从而有效地监测小车机构走行部的健康状态。卑王璐等 [2] 基于自供电式加速度传感器,通过对实测数据的分析,获得轨道车辆一系悬挂装置的振动特征。
数值模拟作为当前科学研究的重要工具,在轨道机械方面得到了广泛应用。李明航和马蒙 [3] 等人基于车辆–轨道耦合频域解析模型,模拟计算车轮不平顺与轨道不平顺联合作用下的轨道频域振动响应;徐磊和翟婉明 [4] 结合车辆–轨道耦合动力学理论和概率方法,建立车轮踏面磨耗的车辆–轨道随机分析模型,较好地分析了不同车轮型面磨损下的动力响应分析及可靠度计算问题;马蒙 [5] 基于车辆–轨道耦合频域解析模型计算了轨道动力响应,比较了不同轮轨激励模式对计算结果的影响;韩鹏和张卫华 [6] 对高速铁路实测型面磨耗量进行研究,提出磨耗预测模型在轮轨接触点、等效锥度、轮轨作用力及车辆安全性等各方面均与线路实测结果具有很好的一致性;肖乾 [7] 基于ANSYS软件研究了不同钢轨打磨处理和轮轨型面匹配对轨道结构振动特性影响,提出了有效改善轮轨接触特性的方法;刘学和张军 [8] 利用多体动力学软件SIMPACK建立高速车辆动力学模型,研究不同磨耗阶段的车轮与3种钢轨型面的动力学匹配问题,分析了轮轨接触几何关系、运行平稳性、振动幅频特性和磨耗数等动力学评价指标;朱海燕和胡华涛 [9] 针对轨道车辆普遍存在的车轮失圆问题,从轨道车辆的稳定性、曲线通过能力、平稳性三个方面阐述车轮失圆对轨道车辆动力学性能的影响;桑平 [10] 建立刚柔耦合的弹性车轮轮对模型,对弹性车轮预装应力与静强度进行了计算分析,研究弹性车轮通过错牙时车轮类型、轨缝长度、运行速度等参量对车轮动力学性能的影响。
本文基于多体动力学软件RecurDyn,采用刚柔耦合接触模型对车轮–轨道体系进行数值模拟。建立车轮–轨道的接触模型,模拟广州港某轨道吊上小车机构在轨道上的运行过程,得到两种不同条件下车轮(正常和踏面剥离)的振动加速度变化情况。同时,在车轮的轴承座上布置加速度传感器,以获取车轮的实时振动加速度。本文的仿真模型可为小车机构车轮的日常维护和检修提供建议和预警。
2. 轮轨刚柔耦合模型仿真
2.1. 仿真算法基础
如果一个机械多体系统通过一系列最小的广义坐标
描述,运动方程就可以表示为一个二阶常微分方程,数学表达式为 [11]:
(1)
式中
为质量矩阵,包含所有体的质量特性和惯性特性;t为时间;
为外力和陀螺力的矢量。在给定t、y、
的条件下,可对公式(1)采用多体系统的拓扑学有效求解出
。
2.2. 模型的简化原则
广州港某轨道吊主要由大梁、小车机构和轨道组成。本文基于车轮–轨道刚柔耦合多体动力学分析小车机构车轮的踏面剥离,将大梁及轨道视为刚体,小车机构视为柔性体。通过三维建模软件SolidWorks建立轨道吊整体模型,以x-t格式导入RecurDyn软件。为了提高计算的精确度,采用ANSYS软件对小车机构进行精确的网格划分,而后将其导入到RecurDyn软件中,其三维模型如图1所示。
由于小车机构在轨道上长期作业,车轮不可避免产生一定程度的磨损,如图2所示。为了简化计算,将小车机构简化为两个车轮和一个连接轴,按照等效原则,将其他部位的质量折算成荷载,施加在车轮和轴承上。建立车轮无缺陷及车轮踏面剥离的模型,如图3所示;采用Solid单元对车轮进行网格划分,车轮踏面缺陷附近的网格尺寸为0.1 mm,其余部位的网格尺寸为5 mm。将小车轨道和车轮模型导入RecurDyn中进行边界条件的设置。
3. 不同类型车轮在轨道上的动力学仿真分析
在长时间的作业过程中,承受交变应力的车轮容易发生金属疲劳现象,导致出现踏面剥离问题,严重时会造成人员伤亡和财产损失。本节仿真分析两种不同类型(正常、踏面剥离)车轮的应力,考察两者应力场的差别;随后,模拟计算两种类型车轮在轨道上运行时的振动加速度,考察踏面剥离情况下车轮振动加速度的周期,为判别小车机构车轮是否存在踏面缺陷提供理论依据。
将小车机构及外载荷均用静力等效的方式施加在车轮上,计算不同类型车轮的应力分布(分别为图4、图5)并提取最大应力,如表1所示。

Figure 3. Finite element model diagram of rail-wheel (left) and local enlargement of contact region (right)
图3. 轨道–车轮的有限元模型图(左)及接触区域的局部放大图(右)

Figure 4. Stress contour of defect-free wheel
图4. 无缺陷车轮应力云图

Figure 5. Stress contour of defect-free tread spallingwheel
图5. 踏面剥离车轮的应力云图
在踏面剥离位置与轨道发生接触时,该部位因几何缺陷而发生应力集中现象,导致其应力分布与无缺陷的车轮有明显的差异。由表1结果可知,踏面剥离的车轮的最大应力要高于无缺陷的车轮,该结果与工程实际情况相符。

Table 1. Maximum stress for two different types of wheels
表1. 两种不同类型车轮的最大应力
广州港某轨道吊小车机构车轮材料如表2所示,仿真结果显示两种车轮的最大应力皆远小于屈服极限 [12]。本文的计算结果与吴岩治 [12]、马蒙和张厚贵 [13] 的结论相符,因此本文的仿真结果具有很好的可靠性,同时表明小车机构车轮处于安全状态。

Table 2. Mechanical parameters of wheel and track
表2. 车轮及轨道的力学性质参数
根据广州港某轨道吊的现场数据,车轮的转动角速度可取为6 rad/s,小车在轨道上行驶的角速度为6 rad/s,据此可在RecurDyn软件中对车轮旋转副Revolute施加驱动为-STEP (TIME, 0, 0, 2, 6),仿真时间设定为10 s。由图6可知,两种类型的车轮在轨道上运行时的振动加速度幅值变化具有显著的差异。无缺陷车轮的振动加速度谱中没有发生跳变现象,幅值稳定保持在−0.2~0.2 m/s2之内,而踏面剥离车轮的振动加速度谱有明显的周期性跳变(周期约为2.5 s)。分析可知,当车轮的踏面缺陷位置与轨道接触时发生撞击,产生的冲击荷载使该位置的振动加速度发生突变,车轮的转动导致该类突变具有周期性。由此可见,两种类型的车轮在轨道上运行时其振动加速度的变化情况不同,踏面缺陷车轮的加速度变化具有明显的周期性。
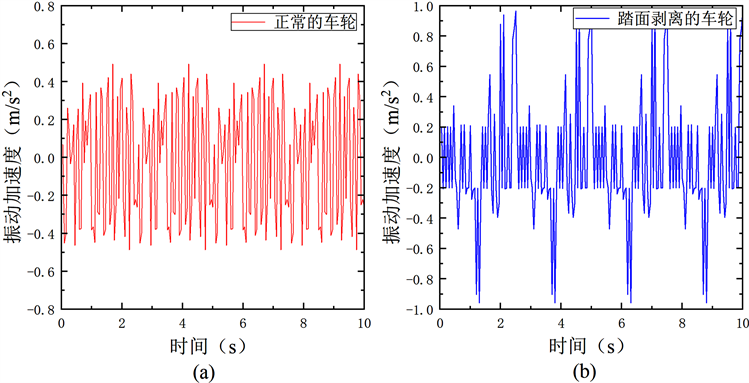
Figure 6. Vibration acceleration spectrum of two types of wheels running on the track ((a) normal wheel; (b) wheel with tread stripped)
图6. 两种类型车轮在轨道上运行的振动加速度谱((a) 正常车轮;(b) 踏面剥离车轮)
4. 实验数据与仿真结果对比
4.1. 现场实验
在存在明显异常振动的车轮上,综合考虑施工安全、线路布置、数据获取等诸多因素,将加速度传感器(品牌为CTC,型号为AC192-1D)安装在车轮轴承座的外端面,如图7所示。

Figure 7. Arranged acceleration sensor
图7. 布置的加速度传感器
4.2. 结果对比
根据加速度传感器的实测数据以及RecurDyn软件的仿真数据,绘制加速度的时域谱图,如图8所示。分析可知,实测数据、仿真数据的加速度幅值存在显著的跳变,且各跳变之间有明显的周期关系(周期约为2.5 s)。结果表明,如果车轮踏面存在剥离,则车轮的振动加速度会产生异常,其幅度与剥离的程度存在一定的关系。
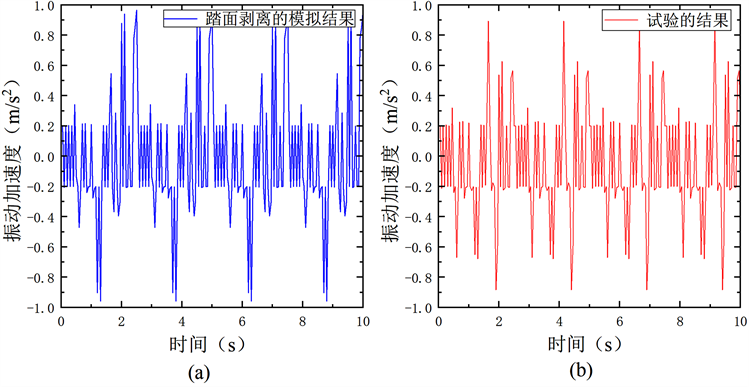
Figure 8. Time-domain spectrogram of vibration acceleration of the wheel with peeled tread ((a) simulation value; (b) test value)
图8. 踏面剥离车轮的振动加速度时域谱图((a) 模拟值;(b) 试验值)
考察存在踏面缺陷车轮的加速度曲线,实测数据与仿真结果非常接近,这验证了RecurDyn数值模拟分析的可靠性。
5. 结论
本文针对广州港某轨道吊的小车机构车轮存在异常振动这一工程实际问题,通过布置加速度传感器获取了车轮的振动加速度;同时,采用多体动力学软件对两种类型车轮(正常和踏面剥离)进行数值模拟分析,获得了相应的应力分布云图以及车轮运行时产生的振动加速度变化情况,得出结论如下:
1) 踏面剥离的车轮的最大应力要高于无缺陷的车轮,但两者均远小于材料的屈服极限;
2) 两种类型的车轮在轨道上运行时,其振动加速度谱的波形具有明显的差异性;
3) 无缺陷车轮在运行时振动加速度稳定保持在一个较小的范围;而踏面缺陷车轮的振动加速度变化具有突变性和周期性;
4) 通过对比仿真结果与现场测试结果,验证了仿真结果的可靠性。本文所提的方法为判断小车机构车轮是否出现踏面缺陷提供了理论依据,为车轮的日常维护和预警提供了数据支撑。
基金项目
湖南省自然科学基金项目(2019JJ50622)。
NOTES
*通讯作者。