求解中国邮递员问题的圈生成算法

Cycle Generating Algorithm for Solving Chinese Postman Problem

摘要: 中国邮递员问题是运筹学与计算机应用邻域的一个重要的基础问题，有着广泛的现实应用。针对有向图上的中国邮递员问题，给出了一种全新的可以直接求解最终回路的非线性整数规划模型，同时提出了一种具有多项式时间计算复杂度的精确求解算法。首先，通过计算所有弧段间的最短路径，得到一个以路径非服务时间为非对角线元素的费用矩阵；接着，将所有弧段构成的集合同时视为一个特殊指派问题的代理与任务集合，并基于前面获得的费用矩阵得到一个指派问题；然后，通过求解上述指派问题，得到遍历网络所有弧段的圈集合；最后，通过搜索圈与圈之间的共用节点，将所有圈合并为一个大圈，从而得到邮递员的最终服务路线。通过理论证明和算例分析，证实了算法的收敛性和多项式时间的计算复杂性。最后对如何处理混合图上的中国邮递员问题进行了讨论，给出了具体求解思路。

Abstract: Chinese Postman Problem (CPP) is an important basic problem in the field of operations research and computer application, and has a wide range of practical applications. For the CPP on directed graph, a new nonlinear integer-programming model that can solve the final loop directly is presented, and an accurate algorithm with polynomial time computation complexity is proposed. Firstly, by calculating the shortest paths between all arcs, a cost matrix with path non-service time as non-diagonal element is obtained. Then, all arcs are regarded as the agents and at the same time tasks of a special assignment problem, and an assignment problem is obtained based on the cost matrix obtained above. Then, by solving the assignment problem above, circles covering all arcs of the network are obtained. Finally, by searching the common nodes between circles, all circles are combined into a large circle, so as to obtain the final service route of the postman. The convergence and the computational complexity of polynomial time of the algorithm are proved by theoretical and numerical analysis. Finally, how to solve the CPP on a mixed graph is discussed, and the corresponding solution process is given.

1. 引言

中国邮递员问题(Chinese Postman Problem—CPP)是1960年由中国数学家管梅谷先生首先提出的 [1]。经过60年的发展，CPP不仅成为一个经典的基础图论问题，而且衍生了许多有重要实用和研究价值的路径问题 [2] [3]。依据网络特征，基本的CPP可分为有向CPP、无向CCP和混合CPP。其中有向CPP和无向CPP所对应的网络分别为有向图和无向图。这两类问题已被证实可在多项式时间计算复杂度条件下求得最优解 [3]。混合CPP问题对应的网络中既包含有向弧段，也包括无向边。混合CPP属于NP-complete问题 [3]。近年来，基于经典CPP，衍生了许多重要的弧路径问题，并在现实中得到了广泛的应用。本文将针对有向CPP给出一种可直接求解最终回路的整数规划模型，并给出一种求解有向CPP的具有多项式时间计算复杂度的算法，并对如何将该算法应用于混合CPP加以说明。

下面对中国邮递员问题(CPP)的研究做一个简介。文献 [1] 给出了求解CPP问题的一种数值求解方法，即奇偶图上作业法。文献 [2] 对中国邮递员问题的提出与研究历史做了回顾。文献 [3] 总结了中国邮递员问题50年研究的历史。在对CPP的拓展方面，文献 [4] 证明了多人中国邮递员问题属于NP完全问题，且具有固定参数的可处理特征。文献 [5] 提出一般化最大收益下的多人中国邮递员问题，并给出了混合整数规划模型，并将理论应用于网络的安全巡视。文献 [6] 针对在给定时间窗内可同时服务部分街道的两侧的情景，构建了相关乡下邮递员问题的混合整数规划模型。文献 [7] 证明了在边着色图上定义的CPP依然可以在多项式时间复杂度条件下求得问题最优解。文献 [8] 针对弧段费用依赖于弧段长度和车辆当前荷载的扩展中国邮递员问题，分析了问题求解的复杂度，建立了相应的优化模型。文献 [9] 针对最大化收益和最小化旅行时间的多目标中国邮递员问题给出了对应的期望值模型。文献 [10] 分析了部分弧段具有遍历优先权的CPP。文献 [11] 给出了一类CPP的拓展问题——混合图上最小最大圈覆盖问题的近似算法。从上述文献简介可以看出，目前针对CPP研究主要是对经典CPP的扩展，如考虑多人问题和多目标问题。而扩展后的CPP问题多数转变为NP-hard问题，但是更加切合相关的具体实践。

在对CPP相关问题的求解方面，研究者分别从经典的整数规划算法、元启发式算法、生物学相关算法、博弈论等多方面进行了深入研究。在利用经典整数规划算法方面，文献 [12] 给出了求解中国邮递员问题的动态规划算法。文献 [13] 给出了如何利用整数规划理论求解边权随机条件下的中国邮递员问题。文献 [14] 给出了求解最大收益中国邮递员问题的分支切割算法。文献 [15] 在弧段旅行时间具有时间依赖性的假设条件下，建构了对应的中国邮递员问题的整数规划模型，并利用割平面法对模型进行了求解。而在利用元启发式方法方面，文献 [16] 考虑邮递员的工作负荷与工作时间约束，给出了混合CPP的遗传求解算法。文献 [17] 将遗传算法应用于带用能力约束的混合中国邮递员问题。文献 [18] 针对弧段费用随遍历次数可变的邮递员问题，给出了两种启发式算法。文献 [19] 分析了弧段旅行时间具有时间依赖性的CPP，并给出了求解该问题的遗传算法。文献 [20] 利用量子退火器对中国邮递员问题进行分析。在利用生物学相关算法方面，文献 [21] 给出了一种基于边权编码方案的中国邮递员问题的DNA计算模型。文献 [22] 给出求解中国邮递员问题的DNA算法。文献 [23] 将生物学中的序列组装问题转化为中国邮递员问题加以分析。文献 [24] 设计了一种具有并行计算能力的生物化学算法来求解中国邮递员问题。合作博弈理论也被用于求解CPP，其中文献 [25] 利用合作博弈理论分析了k-中心中国邮递员分派问题。文献 [26] 利用合作博弈理论分析了多车场中国邮递员问题，并依据是否存在核心平衡匹配对网络进行了分类。从上述的求解算法简介可以看出，针对CPP相关问题的求解，研究者不仅尝试了各种经典整数规划算法，如分支定界和割平面法，而且引入了各种启发式求解算法。尽管这些方法可以有效求解对应的CPP问题，但是在处理其他CPP问题时，需要进行必要的变形，甚至重新设计，因此需要进一步的对比分析，才能明确各种算法的相对效率。

与当前的相关研究不同，本文关注的重点是经典CPP，通过对有向CPP的重新建模，并基于经典指派问题设计了对应的多项式时间算法。通过网络变幻，进而将新算法应用于混合CPP。通过数值算例分析，验证模型与算法的有效性。

2. 模型

2.1. 主要参变量

$G\left(V,A\right)$ 表示一个连通的有向图，包含节点集合V和有向弧段集合A。

$A$ 表示所有需要服务的街道，即有向弧段，构成的集合，其集合势 $\left|A\right|=n$。

$a_1,a_2,a_3\in A$ 表示邮递员需要服务的三条典型街道，即A内的三条典型有向弧段。

$i,j\in V$ 表示网络中联接街道的两个交叉口，即网络中的两个代表节点。

${t^{\prime }}_a$ 表示邮递员途经弧段a并服务a所需要的时间，即弧段a的服务时间。

$t_a$ 表示邮递员途经街道a但无需收集和派送邮件所需要的时间，即弧段a的非服务时间。

$x_a$ 表示邮递员选择的最终回路经过街道a的次数。

$A_i^{+}$ 表示进入节点i的所有街道构成的集合。

$A_i^{-}$ 表示从节点i离开的所有街道构成的集合。

$t_{a,b}$ 表示从弧段a的头节点到弧段b的尾节点的最短路径的非服务行程时间。

$x_{a,b}\in \left\{0,1\right\}$ 指示邮递员是否相继服务弧段a和弧段b。

$y_{a,b}\in \left\{0,1\right\}$ 表示以 $a\in A$ 为代理，以 $b\in A$ 为任务时，两者间是否存在指派关系。

$s\left(a\right)\in \left\{1,2,3,\cdots ,n\right\}$， $\forall a\in A$ 表示在邮递员所走回路中弧段a作为被服务弧段时的序号。

$t_{s\left(a\right),s\left(b\right)}$ 表示如果在最终回路中邮递员相继服务弧段a和b，其值为 $t_{a,b}$ ；否则，其值为0。

$Q$ 表示由特定指派问题的解对应的由服务街道形成的圈的集合，其势 $\left|Q\right|=m$。

$Q_p,Q_q\in Q$ 表示圈集合Q内的两个典型的圈。

2.2. CPP模型

以上面给出的参变量为基础，可以构建如下常见的CPP模型：

$\min {\displaystyle {\sum }_a{t}_a\left(x_a-1\right)}$ (1)

$\underset{a\in A_i^{+}}{{\displaystyle \sum }}{x}_a=\underset{a\in A_i^{-}}{{\displaystyle \sum }}{x}_a,\forall i\in V$ (2)

$x_a\in {\mathbb{Z}}^{+},a\in A$ (3)

上述模型中目标函数(1)表示最小化邮递员的非服务时间。约束(2)表示进入节点 的所有弧段被利用的次数等于所有从该节点离开的弧段被利用的次数。约束(3)表示网络中任何一个弧段至少被利用一次，即为了满足中国邮递员问题的要求：网络中的每一条弧段都要被服务至少一次。上述模型(1~3)是一个典型的线性整数规划问题。通过求解该模型，可以得到网络中每条弧段被利用的次数。但是求解上述模型，并不能得到具体的回路，即遍历各弧段的次序。

为利用优化软件直接求出CPP的最终回路，下面给出一个CPP的非线性整数规划模型：

$\min \underset{a\in A}{{\displaystyle \sum }}\underset{b\in A}{{\displaystyle \sum }}{t}_{a,b}{x}_{a,b}$ (4)

$s\left(a_1\right)\ne s\left(a_2\right),\forall a_1\in A,a_2\in A,a_1\ne a_2$ (5)

$x_{a,b}=\{\begin{array}{ll}1,\hfill & \text{if}s\left(a\right)+1=s\left(b\right)\text{or}s\left(a\right)=n,s\left(b\right)=1\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$ (6)

$s\left(a\right)\in \left\{1,2,3,\cdots ,n\right\},\forall a\in A$ (7)

模型(4~7)中目标函数(4)的含义与前面模型的目标函数(1)的含义一致，表示邮递员回路中总的非服务时间。约束(5)表明任意给定的两条相异弧段在最终回路中具有不同的遍历服务序号。约束(6)定义了当两条弧段被邮递员相继服务时，指示变量 $x_{a,b}$ 的取值。约束(7)限定了在最终回路中弧段序号的取值范围。模型(4~7)是一个带有非线性约束的整数规划模型。如果事先求得 $t_{a,b}$， $\forall a,b$，即可利用现有的商业优化软件，如Lingo，对模型(4~7)直接求解。

3. 求解算法

3.1. 圈生成算法的基本思路

中国邮递员问题(Chinese Postman Problem—CPP)就是给出邮递员从邮局出发，走遍所负责区域内的每条街道最后回到邮局的一条行程时间最短的回路。CPP可根据处理网络的特征分为有向图CPP、无向图CPP和混合图CPP。本研究将针对有向图上的中国邮递员问题给出一个计算复杂度为网络规模三次方的多项式时间求解方法。在本文结论部分将分析如何将该方法推广到处理混合图CPP问题。

当邮递员需要相继服务两条街道时，想要邮递员所走路径的总行程时间最短，邮递员必然要走连接这两条街道的最短路。基于上述考虑，可事先求出网络中所有弧段之间非服务时间最短的路径。如果将网络中需要遍历的弧段既看作一个指派问题的代理，又看作该指派问题的任务，并且规定当代理和任务为同一弧段时，不存在指派关系，就得到了一个特定的指派问题。该指派问题中一个代理与一个任务之间形成指派关系后，对应的任务执行成本等于联接该代理的对应弧段与该任务的对应弧段之间的最短路行程时间。通过求解上述指派问题可以得到联接网络中所有弧段的一个或多个回路。如果上述指派问题的求解结果形成覆盖所有街道(即弧段)的多个圈，根据网络的连通性可以证明这些圈之间必然存在公共端点，而通过这些公共端点可以把这些圈合成一个大圈。合成后的唯一大圈覆盖所有弧段，即为最终的邮递员服务回路。

3.2. 算法的求解步骤

算法的基本流程如图1所示。首先搜索出网络中各弧段间的最短路，建立对应的费用矩阵。以上述费用矩阵为基础将CPP转化为一个特殊的指派问题，并加以求解。再基于指派问题的求解结果确定联接各弧段的圈集合。最后通过确定各圈之间的共用节点，将所有圈合并成一个圈，并输出结果。

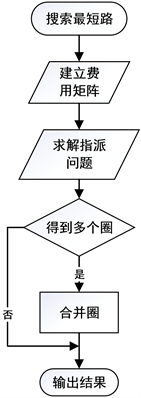
Figure 1. The flow chart of cycle generating algorithm

图1. 圈生成算法流程图

圈生成算法的具体求解步骤如下：

步骤1：搜索弧段间最短路。以非服务时间 $t_a$， $\forall a\in A$ 为弧段旅行时间，运用最短路径搜索算法，如Dijkstra算法，搜索得到网络中任意一对弧段之间的最短路，进而确定 $t_{a,b}$， $\forall a,b,a\ne b$。

步骤2：构造费用矩阵 $C_{n\times n}$，将CPP转化为指派问题。

步骤2.1：用最短路的旅行时间构造一个方阵 $C_{n\times n}$。该矩阵中的元素 $c_{k,l}$， $\forall k,l\in A$ 表示从街道 $a_k$ 到街道 $a_l$ 的旅行时间 $t_{a_k,a_l}$，并令矩阵的对角元素 $c_{k,k}=\infty$， $\forall a_k\in A$。

步骤2.2：以费用矩阵 $C_{n\times n}$ 为基础，将弧段集合A中的元素既作为指派问题的代理，又作为指派问题的任务，可构建如下的经典指派问题模型：

$\min \underset{a\in A}{{\displaystyle \sum }}\underset{b\in A}{{\displaystyle \sum }}{c}_{a,b}{y}_{a,b}$ (8)

$\underset{a\in A}{{\displaystyle \sum }}{y}_{a,b}=1,\forall b\in A$ (9)

$\underset{b\in A}{{\displaystyle \sum }}{y}_{a,b}=1,\forall a\in A$ (10)

$y_{a,b}\in \left\{0,1\right\},\forall a\in A,b\in A$ (11)

步骤3：求解指派模型(8~11)。可利用经典的匈牙利算法求解上述指派问题，从而确定 $y_{a,b}$， $\forall a\in A$， $b\in A$ 的值。

步骤4：从指派问题的解获取联接所有弧段的圈集合Q。求解模型(8~11)后，可以得到变量 $y_{a,b}$， $\forall a\in A$， $b\in A$ 的值。如果 $y_{a,b}=1$， $\forall a\in A$， $b\in A$，表明邮递员需相继服务弧段a和b。考虑到费用矩阵的对角元素值为无穷大，易知 $y_{a,a}=0$， $\forall a\in A$。综上，可知在一个弧段数量有限的网络中，邮递员服务完一条弧段后必然转向服务其他的弧段，直至回到开始弧段的起点。因此利用指派问题的解，可以得到联接了网络所有弧段的一个或多个圈。

步骤5：圈的合成。如果步骤4得到的结果是一个圈，则终止运算，并输出结果；否则，需要对得到的多个圈进行合圈操作，具体步骤如下：

步骤5.1：遍历所有圈，为当前圈所包含的所有节点记录下当前圈的序号。

步骤5.2：遍历所有节点，合并以当前点为共用点的圈。当两个圈合并以后，更新后续节点的相关圈记录。如果两个圈还共用另外的节点，在该节点处两圈的序号被新合成圈的序号取代。其他情况下，原有两个圈的序号均需被新得到的合并圈的序号所取代。

下面以一个具有7条弧段的网络为例对上述步骤4中获取圈集合的过程加以说明。这里假设7条弧段分别用 $a_1,a_2,a_3,a_4,a_5,a_6,a_7$ 表示。假设对应指派问题求解结果中 $y_{a,b}=1$， $\forall a\in A$， $b\in A$ 的变量构成集合 $\left\{y_{1,2},y_{2,4},y_{4,7},y_{7,1},y_{3,5},y_{5,6},y_{6,3}\right\}$。以7条弧段分别作为指派问题的代理与任务，则对应的指派问题二部图如图2所示。该二部图中相同元素之间从左到右的费用无限大，表明无法形成指派关系，在图中以虚线表示。对于实际发生指派的左右两个不同元素，在图中以自左向右的带箭头的有向实线表示。为了形成圈，在图2中相同的弧段以自右向左的有向实线加以联接。根据图中有向实线的连接关系，可以得到两个圈，对应的弧段序列分别为 $a_1\to a_2\to a_4\to a_7\to a_1$ 和 $a_3\to a_5\to a_6\to a_3$。

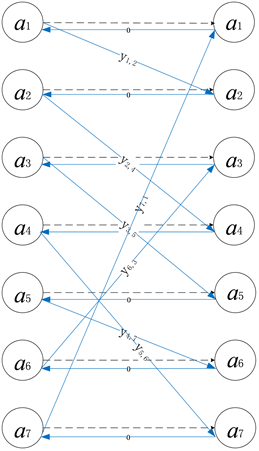
Figure 2. The bipartite graph of assignment problem

图2. 指派问题二部图示意图

如果得到的满足 $y_{a,b}=1$， $\forall a\in A$， $b\in A$ 的变量构成集合 $\left\{y_{2,4},y_{4,5},y_{5,7},y_{7,6},y_{6,3},y_{3,1},y_{1,2}\right\}$，依据相同的操作规则，易知最后得到的是一个圈。

下面以一个例子对上述步骤5中的合圈操作加以说明。如图3所示，假设经过步骤4后得到了2个圈，其中圈1依次经过节点1、2和3，圈2依次经过节点2、4和5。遍历后可得各节点对应的圈序号，其中节点2被两个圈共用。圈合成后邮递员的行走路线必然为从其中一个圈(假设此处为左面的圈1)上的任意一点1出发到交点2，再由交点2出发经过点4和点5，遍历第二个圈后回到交点2，最后由交点2经过点3返回起点1。两个圈合成后的邮递员行走轨迹可表示为节点序列 $\text{1}\to \text{2}\to \text{4}\to \text{5}\to \text{2}\to \text{3}\to \text{1}$。

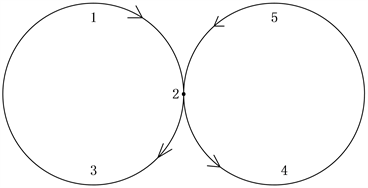
Figure 3. The sketch of combining two cycles

图3. 两个圈的合成示意图

3.3. 算法的性质定理

定理1：假设网络的节点总数为 ，而弧段总数为 ，令 $l=\max \left\{n,k\right\}$，则圈生成算法的计算复杂性为 $O\left(l^3\right)$。

证明：在执行算法的步骤5时，首先相当于遍历所有的网络弧段(对应步骤5.1)，然后是遍历所有的节点(对应步骤5.2)，因此该步骤的计算复杂度为 $O\left(k\times n\right)$。而求解网络中所有节点对之间最短路的算法复杂度为 $O\left(k^{\text{3}}\right)$，而求解指派问题的复杂度为 $O\left(n^{\text{3}}\right)$。基于上述分析，易知圈生成算法最终的计算复杂度是 $O\left(l^3\right)$。

引理1：求解特定指派问题(8~11)所得到的指派结果一定对应一个或多个回路(或言圈)。

证明：由目标函数(8)和与指派问题对应的费用矩阵对角元素值为无穷大易知本命题成立。

引理2：引理1中所述的回路(或言圈)之间存在共用节点，即任意一个圈和其余圈中的至少一个之间存在至少一个共用节点。

证明：如果引理1中所述的圈集合包含两个或以上多个圈，那么可以将其中一个圈与其他圈视为对网络所有弧段的一个划分的两个部分。考虑到网络的连通性，易知对覆盖所有弧段的一个网络划分的两个部分必然存在共用节点，因此上述命题成立。

定理2 (算法的收敛性)：圈生成算法一定可以得到遍历网络所有边至少一次的一条回路，且该回路总的非服务时间最短。

证明：由圈生成算法的求解过程可知，最后得到的圈必然遍历网络中的所有弧段至少一次；而特定指派问题的目标函数等价于CPP问题的优化目标，即最小化将所有弧段连接的最短路的总的非服务时间；综上，可知本命题成立。

4. 算例分析

本节将通过两个算例来验证圈生成算法的有效性。算法利用Java语言实现，在NetBeans IDE 8.0.2开发环境下运行，采用的计算机处理器为Intel® Core i3-3120M CPU。第1个算例的网络如图4所示，包含了6个节点，14条弧段。箭头上的数字表示弧段的序号，小括号内的数字表示弧段的旅行时间(单位：分钟m)。两个弧段如果是对向的话，它们的旅行时间相等。为便于分析，假设所有弧段的服务时间和旅行时间相等。

Figure 4. Network with 6 nodes

图4. 具有6个节点的网络

通过计算可以得到各弧段之间最短路的非服务时间矩阵如图5：

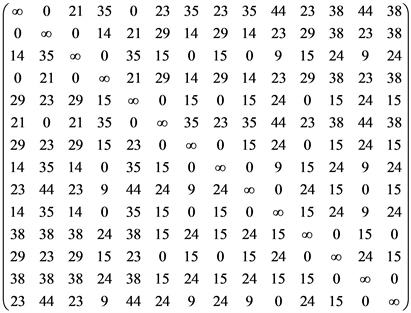
Figure 5. The matrix of shortest non-service times between links

图5. 弧段间的最短非服务时间矩阵

根据圈生成算法计算可得到三个初始圈。圈1包括的弧段序列为{4, 1, 2, 3, 7, 11, 14, 13, 12, 8}；圈2包括的弧段序列为{9, 10}；圈3包括的弧段序列为{5, 6}。合并后得到的最终圈所包括的弧段序列为{11, 14, 13, 12, 8, 4, 1, 2, 3, 9, 10, 7, 6, 5}。最终圈的总旅行时间是224分钟。计算耗时小于计算机可显示的千分之一秒。

对于上述算例，利用Lingo商业优化软件对相应的优化模型(4~7)加以直接求解，经1,433,547次迭代计算，耗时339秒，得到一个局部最优解。该局部最优解对应的最终圈的旅行时间是454分钟，其中非服务时间为230分钟。最终圈的弧段序列如下：1 ® 4 ® 9 ® 13 ® 3 ® 8 ® 7 ® 10 ® 5 ® 12 ® 14 ® 11 ® 6 ® 2 ® 1。与上述弧段序列相对应的弧段间最短路的非服务时间序列为：{35, 14, 0, 38, 15, 0, 24, 35, 15, 15, 24, 15, 0, 0}。

作为对比，下面针对图1的路网，分析如果弧段7不存在的情况。在该情景下，由于弧段7被删除，现在网络中点3和点4的出入度不再相等；因此邮递员想要遍历所有的弧段就需要走重复路段。利用圈生成算法可得到两个初始圈。其中，圈1包括的弧段序列为：{8, 9, 13, 12, 6, 5, 11, 14, 10, 9, 13, 12}。显然这里邮递员需重复经过弧段9，3和12分别两次。这是因为弧段10的头节点到弧段8尾节点之间没有直接连接的弧段。当邮递员需相继服务上述两个弧段时，就需要搜索出从弧段10到弧段8的最短路。经计算可知该最短路包括的弧段有弧段9，3和12。圈2包括的弧段序列为{1, 2, 3, 4}。合并后的最终圈的弧段序列为{9, 13, 12, 6, 5, 11, 14, 10, 9, 13, 12, 8, 4, 1, 2, 3}。该圈的旅行时间是248分钟，其中非服务时间为39分钟。计算耗时小于计算机可显示的千分之一秒。上述两个情景的计算分析说明圈生成算法既可以处理网络中每个点出入度相等的情况，也可以处理不相等的情况。

利用Lingo求解上述情景下的优化模型(4~7)，经1,688,761次迭代，耗时149秒，可得到模型的一个局部最优解。该局部最优解对应的圈的旅行时间345秒，其中非服务时间为136秒。圈包含的弧段序列为：1 ® 2 ® 3 ® 4 ® 5 ® 14 ® 10 ® 11 ® 13 ® 12 ® 6 ® 8 ® 9 ® 1；对应的弧段间最短路的非服务时间序列为{0, 0, 0, 21, 15, 0, 39, 15, 0, 0, 23, 0, 23}。

下面分析图6所示的路网。该路网包含了23个节点，64个弧段。路网中各弧段的旅行时间见表1。表1中，a表示需要服务的弧段， $t_a$ 表示弧段a的非服务时间。为简化表格，假设如果一个弧段的序号为奇数n，那么对应的偶数序号的弧段n + 1的非服务时间和弧段n的非服务时间相等。

Figure 6. Network with 23 nodes

图6. 具有23个节点的路网图

Table 1. The travel time of links in Figure 6

表1. 图6中各弧段的旅行时间

利用圈生成算法可以首先得到遍历网络所有弧段的8个初始圈。圈1包含的弧段序列为{47, 64, 62, 60, 52, 49, 53, 54, 50, 40, 37, 41, 45, 57, 58, 46, 4}；圈2包括的弧段序列为{59, 56, 55, 61, 63, 48, 44, 42, 36, 35, 38, 39, 51}；圈3包括的弧段序列为{15, 18, 19, 27, 28, 20, 17, 16, 6，5, 12, 8, 9, 25, 31, 32, 26, 10, 7, 11}；圈4包括弧段23和24；圈5包括弧段33和34；圈6包括的弧段序列为{1, 2, 3, 4}；圈7包括的弧段序列为{21, 29, 30, 22}；圈8包括弧段14和13。合并后可得到一个最终圈，包括的弧段序列为{19, 27, 28, 20, 17, 16, 6, 5, 12, 8, 9, 25, 33, 34, 31, 35, 38, 39, 51, 59, 56, 55, 61, 63, 64, 62, 60, 52, 49, 53, 54, 50, 40, 37, 41, 45, 57, 58, 46, 43, 47, 48, 44, 42, 36, 32, 26, 23, 24, 10, 4, 1, 2, 3, 7, 11, 15, 21, 29, 30, 22, 18, 14, 13}。最终圈的旅行时间是4196分钟。本例的计算耗时小于计算机可显示的千分之一秒。利用Lingo软件对相应的优化模型加以求解，经3小时计算未得到问题的可行解。因此在此不再给出对应的计算结果。

5. 混合CPP的网络变幻求解

前面的模型与算法是针对有向CPP，事实上可以通过网络变换，利用本文给出的方法处理混合CPP问题。具体的做法如下：

步骤1：将混合图中的无向边转化为两条对向的有向弧段，并假设有向弧段的服务与非服务时间与原来的无向边相等。如 $\left(i,j\right)$ 和 $\left(j,i\right)$ 表示由连接节点和的无向边转化得到的两条有向弧段。 $\left(i,j\right)$ 表示一条以节点 为尾节点，以节点j为头节点的有向弧段。

步骤2：对于一条无向边转化后的两条有向弧段分三种情况加以处理。三种情况的前两种为仅一条有向弧段被采用，另一条对向弧段被忽略；第三种情况为两条转化得到的对向弧段均被采用。如果网络中的无向边有k条，而上述处理带来的组合数目为k³。本步骤就是逐一遍历k³种组合中的所有组合。

步骤3：调用3.2节的算法对上一步得到的有向CPP进行求解。

步骤4：将步骤3得到的结果与当前已知最佳结果加以比较，更新最佳结果。

步骤5：如果k³种组合方式已经全部被遍历，则输出当前最佳结果；否则，转步骤2，选择新的转化弧段采用组合。

有具体步骤间的嵌套调用关系易知上述算法的执行时间将是求解有向CPP子问题时间的k³倍。如果网络中仅含有少量无向弧段时，即上面k的值较小时，上述算法的计算时间应与求解有向CPP子问题的时间相当；而当k值较大时，算法的执行时间将迅速增加。

6. 结论

本文给出了有向CPP问题的一个全新整数规划模型，该模型具有良好的解释性，可以通过现代商业优化软件直接求解得到CPP的邮递员最终服务回路。通过将有向CPP转化为特殊的指派问题求解，给出了一个3次多项式时间计算复杂度的求解方法。通过网络变幻，新的算法也可应用于求解混合CPP。理论证明和数值算例证明了新模型与方法的合理性和有效性。新模型与方法提供了求解CPP相关问题的新思路，可以推广到求解乡下邮递员问题和一般的弧路径问题。

基金项目

国家自然科学基金/National Natural Science Foundation of China (71801153, 71871144)；上海市自然科学基金项目/Natural Science Foundation of Shanghai (18ZR1426200)。

NOTES

^*通讯作者。