1. 引言
近年来,带有弱奇异核的积分微分方程在连续介质力学、热力学、电动力学和种群生物学等领域得到了广泛的应用 [1],因此受到广大学者的关注和研究。针对这类方程,Hu等 [2] 提出向后有限差分方法,并证明了数值格式的稳定性和收敛性,Mohebbi等 [3] 提出高阶紧致差分格式,Chen等 [4] 提出了积分微分方程的二阶BDF交替方向隐式差分格式,Slodicka等 [5] 利用向后差分和线性有限元方法研究带有弱奇异型记忆项的抛物型方程。
本文考虑如下带有弱奇异核的分数阶积分微分方程:
(1)
其中
,
,
是关于t的分数阶Caputo导数:
(2)
是关于t的分数阶 Riemann-Liouville积分:
(3)
在本文中,我们利用Sinc-Galerkin方法离散方程(1)中的四阶偏导项。Sinc-Galerkin方法最初是Stenger [6] 在研究Whittaker基数的基础上提出的,并应用该方法求解二阶微分方程。Smith等 [7] 深入研究了该方法,证明了该方法的收敛速率为
,给出相关矩阵的性质,并利用该方法求解了四阶微分方程。此后有关Sinc-Galerkin方法的研究与应用大量涌现出来。Zarebnia等 [8] 利用该方法研究Troesch问题,并验证了Sinc-Galerkin的指数收敛速度。El-Gamel等 [9] 利用Sinc-Galerkin方法求解六阶两点边值问题,并验证了算法的有效性。Rashidinia等 [10] 在研究非线性两点边值问题中比较Sinc-Galerkin方法和Sinc配置方法,根据数值算例发现两种方法精度基本一致。Qiu等 [11] 利用该方法求解四阶偏积分微分方程,并将相关性质进行了推广。
2. 预备知识
将区域[0,T]均匀剖分,设
为时间步长,令
,
。为了方便,假设本文中的
均为不依赖变量的正常数,符号
表示与参数
有关的正常数。记
。接下来给出分数阶Caputo导数的L1格式。
引理2.1 [12] 假设
,
,则有
(4)
其中
,
。
为了离散
处的分数阶Riemann-Liouville积分
,下面给出梯形卷积求积公式 [13]
(5)
其中权
可以通过
得到,修正权
。
引理2.2 [4] 令
,
,
在区间
连续可导,
。当
,则存在常数C,使得
(6)
引理2.3 [11] 假设
,
,则对于
和
有
(7)
接下来,介绍Sinc函数及其相关性质。在实轴
上,Sinc函数的定义为
(8)
给定步长h,第k次平移的Sinc函数为
(9)
令v为定义在实轴上的可解析的有界函数,若级数
收敛,则
为函数v的Whittaker基数展开式,且有
。为了近似有限区间
上的函数
,引入映射
(10)
且有
,
。映射
将区域
(11)
映射到能够推导出Whittaker基数展开式性质的区域
(12)
因此有限区间上Sinc方法的基函数可以表示为
(13)
区间
上的Sinc方法网格节点为
(14)
应用Sinc-Galerkin方法求解问题会得出加权内积项,接下来我们介绍Sinc梯形求积公式的定义和相关性质。
定义2.1 [7] 令函数
为
的逆映射,
为在区域D上可解析的函数F的集合,且满足
(15)
其中
,且在边界上(记为
)满足
(16)
定理2.1 [7] 令
,
,给定充分小的h,则有
(17)
其中
(18)
利用
,可以得到
。
定理2.2 [7] 假设
,
,
为正常数,函数F和
的定义与定理2.1一致,则有
(19)
因此有限项Sinc梯形求积公式可改写为
(20)
其中
。令
,
(这里
表示下取整),则有
(21)
引理2.4 [7] 令
,
,
,则Sinc导函数在节点处的值为
(22)
引理2.5 [7] 令
,
,对于
,
,有
(23)
其中
(24)
3. Sinc方法的离散格式构造及收敛阶分析
3.1. 半离散格式
记
,
,
,
,
。利用引理2.1和引理2.2则方程(1)在
的半离散格式为
(25)
且很容易得到
。
3.2. 全离散格式
Sinc方法的逼近格式为
 (26)
(26)
其中未知系数
通过对残差正交化得出,即
(27)
这里
为加权内积,其中权函数
的选取与偏微分方程的边界条件,定义的区域有关 [7]。为了利用Sinc求积公式逼近积分项,这里采取另一种分析方法:
(28)
因此上式中的加权内积项可以被定理2.1和定理2.2精确逼近。
我们首先讨论
,利用四次分部积分得到
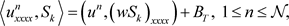 (29)
(29)
其中
表示
内积,且边界项
为
(30)
应用定理2.1中的求积公式可得
(31)
其中积分误差项
是将式(17)中的F替换为
得到的。这里为了计算方便,将无限项求和截取为从-M到N的有限项求和。假设
,选取合适的权函数,使得
,利用
的定义,可以得到
(32)
其中
(33)
同理得到剩下的积分的逼近格式
(34)
其中G为(28)中的
,
,
,
或
,积分项误差
是分别将式(17)中F替换为
,
,
,
和
得到的。
假设
为方程(1)的近似解,记
为
,令
,
,
。令
,则确定未知系数
的Sinc-Galerkin全离散格式为
(35)
记
为对角线上元素为
的
阶对角矩阵,
,
,
,
。令
,
,
。则可以得到式(35)的矩阵形式:
(36)
3.3. 收敛阶分析
给定函数
满足定义2.1,函数
满足引理2.5,
满足(34),对于(28),利用定理2.1和引理2.5可以得到
(37)
和
(38)
在实际计算中,我们需要将式(37)中的无限项求和截断为有限项,即
(39)
接着继续分析(39)中级数的截断项,令
,
,通过定理2.2可以得到
(40)
通过引理2.4 和
的定义,得到如下不等式
(41)
结合(39),(40)和(41),可以得到
(42)
其中
,同理对另一侧截断级数分析可以得到
(43)
因此,将(42)和(43)代入(39),得到
(44)
这里选取
,
,注意到
,结合引理2.5有
(45)
因此
,且有
(46)
其中
。最后讨论带有权和修正权的误差估计,结合引理2.3,(44)和(46),可以得到
(47)
和
(48)
注意到
,
,
有界,结合上述证明,可以得到(28)中其余积分项的估计。为了表述方便,其结果由下述定理给出。
定理3.1令映射
,Sinc网格节点
,函数
,函数
,集合
的定义与前文一致,给定l,
,
,选择
,
,对于式(28)中的每一个积分项有如下估计:
1) 令
,
,则有
(49)
2) 令
,则有
(50)
3) 令
,则有
(51)
4) 令
,则有
(52)
5) 令
,
,则有
(53)
6) 令
,则有
(54)
(55)
定理3.1 给出方程(1)的Sinc-Galerkin全离散格式的精确估计。令
,则全离散格式的收敛阶为
。
4. 数值实验
定义误差的无穷范数为
时间和空间上的收敛阶分别为
(56)
下面通过一个数值算例验证收敛阶。给定区域
,令
,
,取
,
,则空间上的误差为
。Sinc-Galerkin方法的权函数为
,记
为Beta函数,令精确解为
,对应的源项为
(57)
首先计算
范数下的时间误差和收敛阶。在空间上令
,选择不同的
进行验证,结果如图1和表1所示。在表1中分别选择
,
和
,
得到
范数下的时间误差和收敛阶。在图1中,分别画出了数值模拟和理论估计在时间上的收敛阶图像。结合表1的数据和图1的结果来看,在时间上收敛阶与理论分析一致。接着令
,选择不同的M得到相应的空间Sinc点,完成数值模拟。接着选择四组不同的
验证,在表2中得到四组
范数下的空间误差和收敛阶。选择
,
,在图2中得到空间上的收敛阶曲线并与理论估计值比较。综合来看,在空间上收敛阶与理论分析也一致,均为指数收敛。

Table 1. The maximum-norm errors, temporal convergence rates with different α , β when M = 32
表1.
,
范数下的时间误差和收敛阶

Table 2. The maximum-norm errors, spatial convergence rates with different α , β when N = 10000
表2.
,
范数下的空间误差和收敛阶
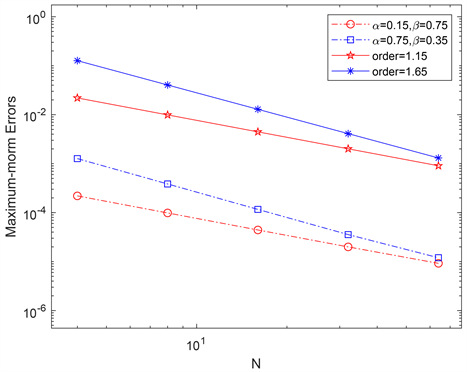
Figure 1. The temporal convergence rates when
图1.
时得到的时间收敛阶
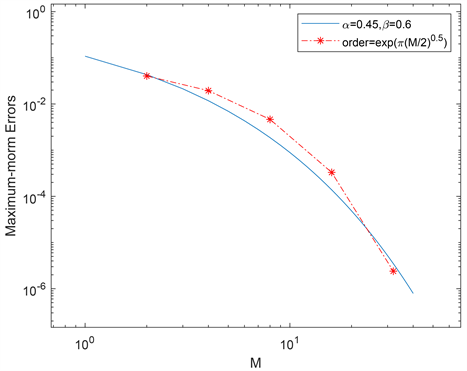
Figure 2. The spatial convergence rate when
图2.
时得到的空间收敛阶
5. 结论
本文中,我们利用Sinc-Galerkin方法求解带有弱奇异核的四阶偏积分微分方程。在时间上利用L1格式和梯形卷积求积公式分别离散分数阶导数和积分。在空间上针对四阶导数的复杂性,利用Sinc-Galerkin方法去近似它。相较有限差分方法,Sinc-Galerkin方法通过较少的点近似高阶导数并可以达到指数收敛。最后我们通过数值算例证明方法的准确性和有效性。结果表明,在空间上利用较少的点即可达到较高的精度,且收敛阶与理论估计一致,再一次证明方法的准确性和有效性。相比之下时间上的精度还不够理想,在今后的研究中我们将考虑分数阶算子的其他差分格式,使时间上的精度得到提高。