1. 引言
大部分多重处理器系统都以互连网络作为基本的拓扑结构并且通常用图来表示一个互连网络,其中顶点代表处理器,边代表处理器之间的通信链路。我们用图和网络互换。对于多重处理器系统来说,其网络拓扑性质的研究是非常重要的。诊断度是度量多重处理器系统故障诊断能力的重要参数,它是互连网络中热门的研究课题之一。此外,在系统中,一些处理器可能是故障的。所以,为了保证计算机系统的可靠性,系统中的故障处理器应该被诊断出来,处理故障系统的第一步是故障识别,在多重处理器系统中存在的故障处理器在此步中一一被识别出来,这一识别过程被称为系统的诊断。在之前的研究中,研究者已经提出了许多系统诊断模型,其中被广泛使用的是比较模型(MM模型)。MM模型是由Malek和Maeng [1] 首次提出的。后来,Sengupta和Dahbura [2] 提出了MM*模型,它是MM模型的一个特例。Dahbura和Masson [3] 提出了一个时间复杂度为
的算法。在故障处理器的数量不超过t的情况下,如果所有故障的处理器能够被识别出来并且不被替换,我们就称这个系统是t-可诊断的。一个系统G的诊断度
是使得G是t-可诊断的t的最大值 [4] [5] [6] [7]。
在之前的研究中,人们一直考虑的是一个多重处理器系统的全局诊断度。在文献 [8] 中,Hsu和Tan首次提出了一种测量多重处理器系统G的局部诊断度的概念。这种新的概念研究的是每个处理器的局部性质而不是全局性质。如果我们只考虑全局故障或无故障状态,我们就会失去系统的一些细节。在文献 [9] 中,Chiang和Tan提出了一种有用的确定系统诊断度的新方法,即延展星结构法。该方法可以保证节点的诊断性,并给出了比较诊断模型(MM模型)下局部可诊断性的充分条件,他们发现在局部诊断性和传统的诊断性之间存在很强的关系。如果系统G中每个点的局部诊断性等于它的度,那么系统G具有强局部诊断性。根据这个概念,强局部诊断性被广泛研究。在文献 [10] 中,Chiang等人证明了
维星图的诊断性是
,且即使它存在
条遗失边,仍保持强局部诊断性。后来,Cheng等又研究了置换树生成的Cayley图 [11] 和
星图和2树生成的Cayley图 [12]。在2018年,Wang和Ma [13] 证明了交错群图
在MM*模型下即使存在
条遗失边,仍保持强局部诊断性。2020年,Wang和Ma [14] 证明了排列图
在MM*模型下即使存在
条遗失边,仍保持强局部诊断性,且证明了
是最优值。2020年,Zhou [15] 等人证明了扩展k元n立方体
在比较模型下即使存在
条遗失边,仍保持强局部诊断性。2020年,Feng [16] 等人证明了轮图
在MM*模型下即使存在
条遗失边,仍保持强局部诊断性,且证明了
是最优值。2021年,Fan [17] 等人证明了
在MM*模型下即使存在
条遗失边仍具有强局部诊断性,并且证明了
是最优值。同时,他们证明了
在MM*模型下即使存在
条遗失边仍具有强局部诊断性,并且证明了
是最优值。
k元n立方体
有许多良好的性质。比如点传递性 [18],边传递性 [19],小直径 [20] [21] 等。在这篇文章中,我们证明了
的诊断度是2n,且在MM*模型下即使存在
条遗失边,仍保持强局部诊断性并且是最优的。
2. 基本概念
多重处理器系统被表示为一个无向的简单图
,其中
,
,分别表示图G的顶点集和边集,且顶点集
代表处理器,边集
代表处理器之间的通信链路。对于任意的非空顶点子集
,则以两端点均在
中的边的全体为边集所组成的子图,称为
在G中的导出子图,记作
。
是指G中与v关联的边的数目,
表示G中顶点的最小度。对于G中任意一个顶点v,都有
,则称图G是k-正则的。对于任意
,
表示G中与v相邻的所有顶点组成的集合。对于
,u称为v的一个邻点。对于邻集、度等这些概念,在没有歧义产生时,我们通常省略图的下标。G的一条途径是指一个有限非空序列
,它的项交替地为顶点和边,使得对
,
的端点是
和
,称P是从
到
的一条途径。
和
分别称为P的起点和终点,整数n称为P的长。若途径P的顶点
互不相同,则P称为路。我们用
表示一条长为n的起点是
,终点是
的路。如果把G的点集任意划分为两个非空子集X和Y,总存在一条边满足其中一个端点在X中,另一个端点在Y中,那么G是连通的。一个图G的连通度
和边连通度
分别是把图G变成一个不连通图或仅一个点所需移除的点和边的最小数量。一个二部图是一个点集能分解成两个子集X和Y的图,使得每条边都有一个端点在X中,另一个端点在Y中,这样的划分
被称为图的一个二分类。一个图
与另一个图
同构(记为
)当且仅当存在一个双射
使得对于任意两个顶点
,
,
。文中其他未定义而直接使用的符号和术语参见文献 [22]。
3. MM*模型
在MM模型中,一个处理器发送同样的任务给一对不同的邻点,然后比较它们的反应结果。一个系统
的比较方案被建模为一个多重图,用
表示,其中L是被标记的边集。一条被标记的边
代表用一个顶点w去比较两个相邻顶点u和v,这意味着
。如果节点w是非故障的(故障的),那么测试结果是可靠的(不可靠的)。如果
且
,则
。如果
且
,则
。如果
且
,则
。如果
,则
。
中所有比较结果的集合称为诊断的症候,用
表示。如果比较
的结果不一致,则
;否则,
。因此,一个症候是从L到
的一个函数。MM*中每个节点必须测试其任意一对相邻节点。即如果
,则
。在系统中,所有故障处理器的集合叫做一个故障集,它可以是
的任意一个子集。在MM*模型下,对于一个给定的症候
,如果对任意的
满足
,
当且仅当
或
或
,则我们称故障子集
和
是一致的。我们用
表示和F一致的所有症候的集合。设
和
是
中两个不同的子集。如果
,则
是不可区分对;否则,
是可区分对。
定义3.1 [15] 一个系统
是t-可诊断的,当且仅当V中每一对不同的故障子集
和
,其中
,
,
是可区分对。
设
,
是
中两个不同子集,对称差
。
定理3.1 [2] [3] 一个系统
在MM*模型下是t-可诊断的,当且仅当对于V的每一对不同的故障集
和
,其中
,
,满足下列条件之一(见图1):
1) 存在
和
满足
,
。
2) 存在
和
满足
,
。
3) 存在
和
满足
,
。
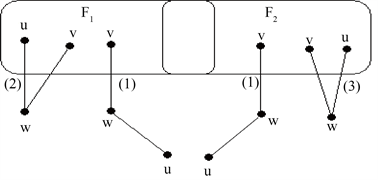
Figure 1. Illustration of a distinguishable pair under the MM* model
图1. 在MM*模型下可区分
4. 局部诊断度
引理4.1 [10] 系统
在x点处是局部t-可诊断的,如果给定一个测试症候
,它是由系统在一组包含x的故障顶点集F的情况下产生的,
,那么故障顶点集
的每一个集合与
一致,且
必须包含顶点x。
引理4.2 [9] 系统
中,如果
且对于V的每一对不同的故障子集
和
是可区分的,其中
,
,则点x是局部t-可诊断的。
引理4.1和引理4.2是等价的。
引理4.3 [10] 一个系统
是t-可诊断的当且仅当G中每个点都是局部t-可诊断的。
引理4.4 [10] 一个系统
中,G中x点是局部t-可诊断的t的最大值被定义为点x的局部诊断度
,即
。
引理4.5 [10] 一个系统
的诊断度
等于G中每个点的局部诊断度的最小值,即
。
定义4.1 [10] 设x是一个图
中的一个点。若
,我们定义一个延展星图
,其中
,点集
,边集
。
注意到x称为
的根。
引理4.6 [10] 设x是系统
中的一个点且
。如果点x在G中存在一个延展星图
,则x的局部诊断度是n。
引理4.7 [23] 设G是一个系统的图表示,那么在MM*模型下,诊断度
。
引理4.8 [10] 设x是图
中的一个点。如果x的局部诊断度等于它在G中的度,即
,则这个点x有强局部诊断性。
引理4.9 [10] 设
是一个图。如果G中每个点的局部诊断度都等于它在G中的度,即对于所有的
都有
,则G有强局部诊断性。
5. k元n立方体
定义5.1 [24] k元n立方体
是一个有
个顶点和
条边的2n正则图。k元n立方体
的顶点u用长为n的二进制字符串表示,如
,其中
,
。两个顶点
和
相邻当且仅当存在一个整数
使得
,同时
对于
。为了陈述清晰,我们在后文中省略了类似“
”的表达形式。
我们将
划分为k个互不相交的子图
(在不产生歧义的前提下可以缩写为
),各子图内每个顶点
在最后一个位置
上有一个固定的整数i,其中
。显然,
同构于
,对于
。6元1立方体,5元2立方体如图2所示。设
,那么
称为u的外邻点集。连接来自不同子图
和
的顶点的边称为外部边,而将连接来自相同子图
的顶点的边称为内部边。
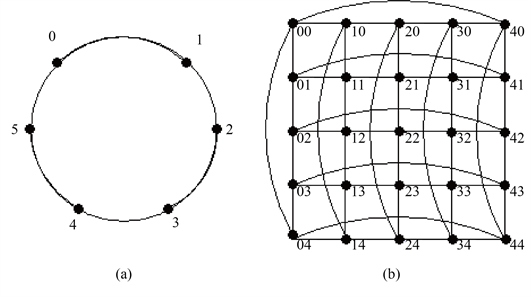
Figure 2. (a)
; (b)
图2. (a) 6元1立方体;(b) 5元2立方体
引理5.1 [18] [19] k元n立方体
是点传递和边传递的。
引理5.2 [18] k元n立方体
是二部图当且仅当k为偶数。
引理5.3 [18] k元n立方体
有下列性质:
(1)
。
(2)
中每个点与
条内部边关联,与2条外部边关联。
(3)
中每个点的两个外邻点在不同的子图中。
6. k元n立方体
的诊断度
引理6.1 对于k元n立方体
中任意一点x,在x点处存在一个延展星图
。
证明 我们可以在x点处找到一个延展星图
作为k元n立方体
的子图。由引理5.1,
是点传递的。不失一般性,设
是延展星图
的根。当
,
时,我们可以在x点处找到一个延展星图
(见图3)。显然,
中的各点均不相同。
假设这个结论对于
成立,即在
中存在一个延展星图
。现在我们证明这个结论对于
也成立,即在
中存在一个延展星图
。我们根据最右边的位置将
划分为
,那么
同构于
。由归纳假设,在
中存在一个延展星图
。由引理5.3,点
,它有两个外部邻点在不同的
中,分别为:
和
。记
是
中的一条3长路,
是
中的一条3长路。我们将
和
都连接到x点,并且将它们与
相结合。因此,我们可以在
中x点处得到一个延展星图
,即在
中x点处存在一个延展星图
。

Figure 3. The first
in
图3.
的第一个延展星图
定理6.1 设
是一个k元n立方体且
,
,则
的诊断度是2n,即
且
有强局部诊断性。
证明 通过引理4.6和引理6.1,
中每个点x的局部诊断度是2n。由引理4.3,
是2n-可诊断的。由
的定义可知,
。由引理4.3和引理4.7,
,即
的诊断度是2n。因为
中每个点x的度是2n,
中每个点的局部诊断度等于它的度。由引理4.8,
中每个点x有强局部诊断性。由引理4.9,
有强局部诊断性。
引理6.2设
是
中任意的遗失边集,
。
中存在一个延展星图
,其中
。
证明 由引理5.1,
是一个点传递图,不失一般性,设
是延展星图
的根。我们通过对n进行归纳来证明这个引理。当
时,我们可以找到五个延展星图
,它们的边除了与x关联的边之外均不相同,其中第一个延展星图与引理6.1的证明中提到的相同(见图3),另外四个延展星图分别如图4~7所示。
因为
,我们只需要考虑有四条遗失边的情况。设
是与x相关联的遗失边的数目,那么
就是不与x相关联的遗失边的数目。如果
,那么
,则存在四条遗失边不与x相关联。由于我们已经找到了五个除了与x关联的边之外都不同的延展星图
,所以我们可以从五个延展星图
中找到一个不包含遗失边的延展星图
。如果
,我们再分情况讨论。当
时,则
。如上所述,我们已经找到了五个除了与x关联的边之外都不同的延展星图
,我们可以从这五个当中至少找到四个除了与x关联的边之外都不同的延展星图
,这样我们就可以找到一个不包含遗失边的延展星图
。当
时,则
。情况类似,我们从已经找到的五个除了与x关联的边之外都不同的延展星图
当中至少找到三个除了与x关联的边之外都不同的延展星图
,这样我们又可以找到一个不包含遗失边的延展星图
。当
时,则
。情况类似,我们从已经找到的五个除了与x关联的边之外都不同的延展星图
当中至少找到两个除了与x关联的边之外都不同的延展星图
,这样我们又可以找到一个不包含遗失边的延展星图
。当
时,则
。情况类似,我们从已经找到的五个除了与x关联的边之外都不同的延展星图
当中至少找到一个除了与x关联的边之外都不同的延展星图
,这样我们又可以找到一个不包含遗失边的延展星图
。由此我们可以得出结论:在具有遗失边
的
中存在一个延展星图
,其中
。

Figure 4. The second
in
图4.
的第二个延展星图

Figure 5. The third
in
图5.
的第三个延展星图

Figure 6. The fourth
in
图6.
的第四个延展星图

Figure 7. The fifth
in
图7.
的第五个延展星图
假设这个引理对于
成立,即在
中存在一个延展星图
,其中
是遗失边集且
。现在我们证明这个结论对于
也成立,即在
中存在一个延展星图
,其中
是遗失边集且
。设
是由
的顶点最后一个位置
诱导的子图,则
同构于
。设
,记
点在
中。由引理5.3,
与两个外部邻点相邻:
和
。设
,
,它们分别在
和
之中。设
,其中
,
,那么
。注意到
,我们有
,其中
。为了证明这个引理,我们首先需要在
中找到一个延展星图
,然后找到两条分别处在
和
中的3长路
和
,我们连接
和
到x,然后将它们与
相结合,这样我们就在
中得到一个延展星图
。我们再考虑以下情形。
情形1
。
由归纳假设,在
中存在一个延展星图
。为方便起见,我们假设
。如果
,那么我们就不需要通过
扩展A。如果
,由引理5.3可知,
。我们再考虑下列情形。
情形1.1
。
在这种情形下,
。y有两个外部邻点
和
。注意到
,
。设
,
。因为
,我们有
且
和
不包含遗失边。我们连接
和
到x,然后将它们与A相结合,这样我们在
中得到一个延展星图
。
情形1.2
。
由引理5.3,
,因此,我们可以得到
是连通的。
,我们可以在
中找到一条以y开头的3长路
,然后将它通过
扩展A。如果
,该情况与之类似,于是我们可以在
中找到一条以z开头的3长路
,然后将它通过
扩展A。如果
,那么
,情况与情形1.1类似,我们可以找到两条3长路
和
。
情形2
且
。
在这种情形下,
。 设
,
,它们分别在
和
中。我们可以找到两条不同的分别以y和z开头的3长路:
,
,
,
。
很显然,
,
,
和
中除了y和z之外没有公共点。因为
,所以在
外部不存在
中的边,因此我们可以从
,
,
和
中选择两条不包含遗失边的3长路
和
。设f是
中任意一个元素,并且
,那么
。由归纳假设,在
中存在一个延展星图
。设
。如果A中不包含f,那么我们可以在
中找到一个延展星图
。下面我们讨论
。
情形2.1 f与x相关联。
在这种情形下,我们通过删除A中包含f的路得到延展星图
。因为
,则我们可以从
,
,
和
中选择两条不包含遗失边的3长路
和
。我们连接
和
到x,然后将它们与
相结合,因此,我们在
中就得到了一个延展星图
。
情形2.2 f不与x相关联。
设
是一条以u开头的3长路,同时假设它包含f,那么u与x相邻。由定义5.1,记
,并且
。不失一般性,设
。由引理5.3,u有两个外部邻点
和
,它们分别在
和
中。因为在
外部不存在
中的边,所以存在一个点
使得
是u的外部邻点,同时
。因此我们只需要找到一条以
开头的2长路。不失一般性,假设
或者
。
情形2.2.1
。
在这种情形下,
。注意到
,
,于是我们可以从
中找到一条以
开头的不包含遗失边的2长路:
。注意到
,且
,因此我们连接
到u即可得到一条3长路
,然后连接
,
和
到x,然后将它们与A相结合,于是可以在
中
得到一个延展星图
。
情形2.2.2
。
在这种情形下,
。注意到
,
,于是我们可以从
中找到一条以
开头的不包含遗失边的2长路:
。注意到
,且
与
之间没有公共点。因此我们连接
到u即可得到一条3长路
,然后连接
,
和
到x,然后将它们与A相结合,于是可以在
中得到一个延展星图
。
情形3
且
。
注意到
。 设
,
,它们分别在
和
中。我们可以找到两条不同的分别以y和z开头的3长路:
,
,
,
。
很显然,
,
,
和
之间除了y和z之外没有公共点。如果
,则在
中最多存在
中的一条边。因此,我们可以从
,
,
和
中选择两条不包含遗失边的3长路。如果
,那么
。在这种情形下,如果
,那么我们从
,
,
和
中选择两条不包含遗失边的3长路。如果
,那么我们从
,
,
和
中选择一条不包含遗失边的3长路。设f是
中任意一个元素,且设
,那么
。由归纳假设,在
中存在一个延展星图
。设
。如果A中不包含f,那么我们可以在
中找到一个延展星图
。下面我们讨论
。
情形3.1 f与x相关联。
我们通过删除包含f的路得到一个延展星图
。假设
,那么
,
。因为
,我们从
,
,
和
中选择两条不包含遗失边的3长路
和
。我们连接
和
到x,然后将它们与
相结合。因此,我们可以在
中找到一个延展星图
。假设
。如果
,那么我们从
,
,
和
中选择两条3长路
和
。我们将
和
这两条路连接到x,然后将它们与
相结合。因此,我们可以在
中得到一个延展星图
。如果
。设
或
。我们通过删除包含
或
的路得到一个延展星图
。我们从
和
中选择一条不包含遗失边的路连接到x,然后将它与
相结合。因此,我们可以在
中得到一个延展星图
。
情形3.2 f与x不相关联。
设
是一条以u开头的3长路,且假设它包含f,那么u与x相邻。由定义5.1,记
且
。不失一般性,设
。由引理5.3,u有两个外部邻点
和
,它们分别在
和
中。因为在
外部存在
中的一条边,所以存在一个点
使得
是u的外部邻点,同时
。因为
。设
,那么
。我们只需要找到一条以
开头的2长路。不失一般性,假设
或者
。
情形3.2.1
。
在这种情形下,
。注意到
,
,我们可以找到两条以
开头的2长路:
,
。
很显然,
,
,
和
中除了
和y之外没有公共点。因为在
之外最多存在
中的一条边,我们可以从
和
中选择一条不包含遗失边的2长路
。我们连接
到u得到一条3长路
,然后连接
,
和
到x,并且将它们与
相结合。因此,我们可以在
中找到一个延展星图
。
假设
。这里,
。注意到
,
,我们可以找到两条以
开头的2长路:
,
。
很显然,
,
,
和
中除了
和z之外没有公共点。因为在
之外最多存在
中的一条边,因此
或者
不包含遗失边。我们从
和
中选择一条不包含遗失边的2长路
。我们连接
到u即可得到一条3长路
,然后连接
,
和
到x,并且将它们与延展星图
相结合。因此,我们可以在
中找到一个延展星图
。
假设
,那么
。 因此,存在一个点
使得
是u的外部邻点且
。不失一般性,假设
。与情形3.2.1类似,我们可以在
中找到一个延展星图
。
情形4
。
在这种情形下,
。设f,
是
中任意两个元素,且
,那么
。由归纳假设,我们可以在
中存在一个延展星图
。设
。
情形4.1 A中不包含f和
。
我们可以在
中找到一个延展星图
。注意到
且
,那么在
和
中不存在
中的边。因此,我们可以在
中找到一条以y开头的3长路
,然后将
与x相连,然后将它与A相结合。
的情况与此类似。因此,我们可以在
中找到一个延展星图
。
情形4.2 A中包含f或
。
不失一般性,我们假设A中包含f。 现在我们讨论f是否与x相关联。如果f与x相关联,证明与情形2.1类似。如果f不与x相关联,证明与情形2.2类似。
情形4.3 A中包含f和
。
如果f和
都与x相关联,那么我们可以通过删除包含f和
的路得到一个延展星图
,接下来的证明与情形3.1类似。如果
中仅有一个与x相关联,不失一般性,设
与x相关联,f不与x相关联。我们可以在
中找到一个延展星图
,接下来的证明与情形2.2类似。如果f和
都不与x相关联,那么我们考虑f和
是否属于同一条路。如果f和
都属于同一条路,证明过程与情形2.2类似。现在我们假设f和
属于A中不同的路。设
是一条以u开头3长路并且假设它包含f。设
是一条以v开头的3长路并且假设它包含
。由引理5.3,每个u和v分别有两个外部邻点且在不同的子图中。假设u和v的一个外部邻点分别是
和
,其中
,
,
且
。注意到
,
,那么在
之外不存在
中的边,因此我们可以分别在
和
中找到一条以
和
开头的2长路
和
,然后将它们分别与
和
相连,我们就得到了不包含遗失边的3长路
和
。因此,我们就完成了在
中找到一个延展星图
的证明。
定理6.2 设
是k元n立方体
中任意边子集且
。对
中的每个点x,
有强局部诊断性,其中
的个数是最优的。
证明由引理4.6和6.2,在
中,每个点x的局部诊断度等于它的度,且
,
,
。由引理4.8和4.9,
有强局部诊断性。现在我们证明
的个数是最优的。
接下来我们举例说明当k元n立方体
存在
条遗失边时不能保证有强局部诊断性。因为
是一个点传递图,不失一般性,假设
。我们假设在
中存在
条遗失边F都与x相关联(见图8),那么在
中x的度就变成了1,即
。很容易知道y是x在
中唯一的邻点。设
,
,此时
。显然,
和
之间是没有边的。由定理3.1和引理4.8,
不满足条件(1)~(3),并且在
中y点在MM*模型下不是2n局部诊断的。然而,
,故在
中y点的局部诊断度(少于2n)不等于它的度(等于2n)。因此,y没有强局部诊断性。故当k元n立方体
有
条遗失边时,它不具有强局部诊断性了。
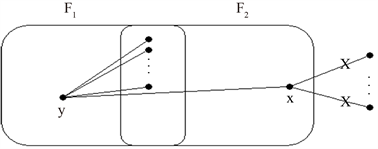
Figure 8. Illustration of the proof in Theorem 6.2
图8. 定理6.2的证明
7. 结论
在这篇文章中,我们研究了k元n立方体
在MM*模型下的局部诊断度。由强局部诊断性的定义 [8],我们证明了k元n立方体
具有强局部诊断性,即使存在高达
条遗失边,它仍保持强局部诊断性。所以,在k元n立方体
的遗失边数不超过
的条件下,它的诊断度等于每个处理器剩余度的最小值。
致谢
本论文是在我的导师王世英教授的亲切关怀和认真指导下完成的。他严肃的科学态度,严谨的治学精神,精益求精的工作作风,深深地激励着我。从课题的选择到项目的最终完成,王老师都始终给予我细心的指导和不懈的支持。在写论文的过程中,王教授不仅在学业上给我精心的指导,同时还在思想、生活上给我无微不至的关怀,在此谨向王老师致以诚挚的谢意和崇高的敬意。同时,感谢与我并肩作战的师兄、师姐以及同门们,感谢关心我,支持我的朋友们,感谢学校领导、老师们,感谢你们给予我的帮助与关怀,谢谢!