1. 引言
非线性发展方程在许多领域中有着广泛的应用,例如在流体力学、固体物理、生物和海洋工程、光纤、等离子体物理和化学物理等领域中,涌现出类似于薛定谔方程 [1] 、KdV方程 [2] 等许多重要的非线性发展方程。如今,人们提出了许多有效的方法去构造非线性发展方程的精确行波解,如
扩展法 [3] [4] ,正弦–余弦方法 [5] ,
函数法 [6] [7] ,Jacobi椭圆函数法 [8] [9] ,tanh函数法 [10] ,扩展的直接代数法及新的扩展的直接代数法 [11] [12] [13] ,
扩展法 [14] [15] ,F-扩展法 [16] [17] ,映射法和扩展映射法 [18] ,
扩展法 [19] [20] [21] [22] 等。
本文主要用
扩展法构造(3 + 1)维修正KdV-Zakharov-Kuznetsov方程 [14] (简称mKdV-ZK方程)
(1)
和(3 + 1)维Kadomtsev-Petviashvili方程 [3] (简称KP方程)的精确行波解。
(2)
方程(1)中包含四项耗散效应
和一个对流过程
。在均匀磁场存在的情况下,方程(1)控制弱非线性离子声波的行为,包括冷离子和热等温电子的等离子体。1970年,Kadomtsev和Petviashvili在研究散色和非线性介质中的非线性波动理论时提出了KP方程,该方程是描述浅水波和等离子声波的方程,且在很多领域都有重要的应用。Zhang Z Y [8] 利用Jacobi椭圆函数展开法得到了方程(1)精确的行波解;Uttam Ghosh [23] 利用修正分数阶子方程方法得到了方程(1)的精确解析解;Md. Nur Alam [24] 利用一种
扩展法获得了方程(1)一些新的和更一般的行波解。Ma W X [25] 总结了方程(2)的行波解和有理解;Zayed E M E [26] 利用
扩展法得到方程(2)的孤立波解和三角周期解;Lu D [27] 运用拟设法获得了方程(2)的孤立波解、冲击波解和奇异波解等。
本文结构为:在第二部分,给出
扩展法的具体步骤;在第三部分,利用
扩展法构造了(3 + 1)维修正KdV-Zakharov-Kuznetsov方程和(3 + 1)维Kadomtsev-Petviashvili方程的精确行波解;在第四部分,对行波解的图形性态进行分析;总结在第五部分。
2.
扩展法的步骤
考虑如下非线性偏微分方程
(3)
令行波变换
(4)
其中c是波速。在方程(3)中用行波变换(4)可得如下常微分方程
(5)
。假定方程(5)有如下形式的解
(6)
其中
为待定常数,n由齐次平衡原则确定,
满足二阶常微分方程
(7)
其中
是参数,方程(7)有如下形式的解 [19]
(8)
将
以及
的各阶导数与方程(7)代入方程(5)中,合并
的次数,得到一个关于
的代数方程组,再借助解(8)可得出方程(3)的精确行波解。
3. 精确行波解
在本部分利用
扩展法构造(3 + 1)维修正KdV-Zakharov-Kuznetsov方程和(3 + 1)维Kadomtsev-Petviashvili方程的精确行波解。
3.1. mKdV-ZK方程的精确行波解
将行波变换(4)代入方程(1)可得
(9)
其中c是波速。对方程(9)积分一次,并令积分常数为零,则
(10)
根据最高阶导数项
与非线性项
的平衡原则,可得
。再由方程(6)可设方程(10)有如下形式的解
(11)
其中
是待定常数,将方程(11)以及
的相关导数与方程(7)代入方程(10),合并同类项令
的系数为0,得到关于
与c的代数方程组为:
(12)
求解上述方程组可得:
(13)
将方程(13)和方程(8)代入方程(11),得出方程(1)有如下形式的双曲函数解:
(14)
由
扩展法得到的双曲函数解(14)的3D、2D图如图1所示,其中
,
为参数,i为虚数单位。
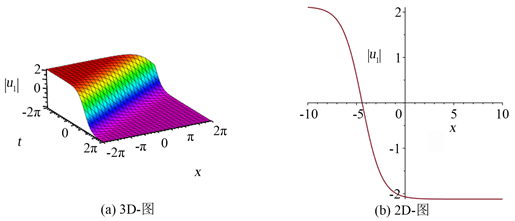
Figure 1. The 3D and 2D plots of solution (14)
图1. 解(14)的3D与2D图
3.2. KP方程的精确行波解
将行波变换(4)代入方程(2)可得
(15)
其中c表示波速。对方程(15)积分两次,令积分常数为零,可得
(16)
考虑
时,
,根据最高阶导数项
与非线性项
的平衡原则,可得
,再由方程(6)可设方程(16)有如下形式的解
(17)
其中
是待定常数,将方程(17)以及
的相关导数与方程(7)代入方程(16),合并同类项令
的系数为0,得到关于
与c的代数方程组为:
(18)
求解上述方程组,得出如下解的情况:
情况1.
(19)
将方程(19)和方程(8)代入方程(17),得出方程(2)有如下形式的双曲函数解:
(20)
其中
。
情况2.
(21)
将方程(21)和方程(8)代入方程(17),得出方程(2)有如下形式的双曲函数解:
(22)
其中
。

Figure 2. The 3D and 2D plots of solution (20)
图2. 解(20)的3D与2D图
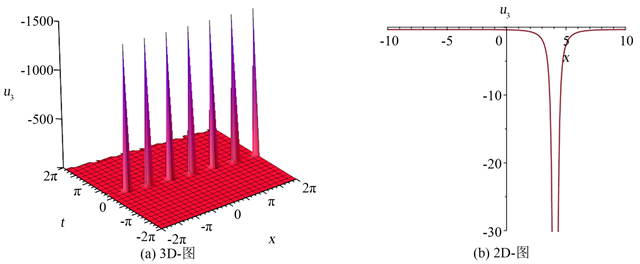
Figure 3. The 3D and 2D plots of solution (22)
图3. 解(22)的3D与2D图
4. 图像分析
图1是方程(1)的解
在
区间内,当参数
时的3D性态,以及
时的2D性态。根据波向右传播,有一个波峰,且波的形状和速度保持不变,可知解
为方程(1)的扭状孤波解。图2是方程(2)的解
在
区间内,当参数
时的3D和
时的2D性态。可以看出解
有一个波谷,并且出现尖点,因此
为方程(2)的非光滑奇异解。图3是方程(2)的解
在
区间内,当参数
时的3D和
时的2D性态。可以观察到解
有一个波谷和尖点,因此
为方程(2)的非光滑奇异解。
5. 总结
本文主要用
扩展法构造了方程(1)和方程(2)的精确行波解,得到方程(1)的解为扭状孤波解,方程(2)的解为非光滑奇异解。做出了这些解在特殊参数值下的3D和2D图,并对这些解的性态进行了分析。
通过将解(14)与文献 [19] 中解(23)比较发现,若解(14)中令
时,可得出解的形式为
,而解(23)中令
,可得出相同形式的解。由此可见,
解(14)比解(23)更具有一般性。
致谢
我对本文进行审阅的各位老师表示由衷的感谢。
基金项目
贵州省科学技术厅基金[2019] (1162)。
NOTES
*通讯作者。