类Samara飞行器的曲线跟踪控制

Curve-Tracking Control of Samara-Like Aircraft

摘要: Samara飞行器是洛克希德·马丁公司在枫树种子的启发下研发的一款单桨旋翼机，它具有体积小、重量轻、气动效率高和隐蔽性强的特点。但是Samara飞行器的控制依赖于独立的视觉跟踪系统，该系统无法机载且价格昂贵，所以对Samara的研究一直处于实验室阶段。本课题组在此背景下，自行设计并制造了一款类Samara飞行器。它摒弃了Samara的视觉传感系统，使用普通民用的传感器和飞控板来进行控制。本文针对类Samara飞行器的曲线跟踪问题，提出了一种基于控制的建模方案，给出了曲线跟踪控制律。仿真结果表明，所设计的跟踪控制律能够使类Samara飞行器以较高的精度跟踪预设轨迹曲线。

Abstract: The Samara aircraft is a single-propeller rotorcraft developed by Lockheed Martin inspired by maple seeds. It has the characteristics of small size, light weight, high aerodynamic efficiency and strong concealment. But the control of the Samara vehicle relies on an independent visual tracking system, which cannot be airborne and is expensive, so research on Samara has been in the laboratory stage. Under this background, our research group designed and manufactured a Samara-like aircraft. It abandoned Samara’s visual sensing system and used ordinary civilian sensors and flight control boards for control. In this paper, a control-based modeling scheme is proposed for the curve tracking problem of Samara-like aircraft, and the curve tracking control law is given. The simulation results show that the designed tracking control law can make the Samara-like aircraft track the preset trajectory curve with high precision.

1. 引言

枫树种子在每年的春天会像直升机一样旋转着飘落，有时在风的驱动作用下其能够靠着自身的稳定旋转飞向很远的地方。在枫树种子的启发下，2008年，洛克希德·马丁先进技术实验室的研发团队研发了一种独特的单桨旋翼机——Samara [1]。Samara主要由推进系统、机翼、机身和机翼后缘的副翼四部分组成，它的旋转半径约为30厘米，具有体积小、重量轻、气动效率高、隐蔽性强的特点，能在1公里的范围内续航20 min，在特定情况下可以完成短程的市区监控以及采样的任务 [2]。并且Samara使用高速图像传感器和光流算法相结合的方法，计算出飞行器此时的运动参数，具有极高的精度 [3]。

在Samara问世后，国外马里兰大学的Ulrich等人对Samara的翼型横截面进行了改进 [4]，研究了翼型对Samara自转效率的影响 [5]，并使用六自由度建模的方法提出了Samara飞行器俯仰和偏航的控制方法 [6]。国内最早由解放军航模队的刘立天等人做过类似的航模，名为“飞行大刀” [7]，但它只能随风飞行，而不能自主控制飞行。南京航空航天大学国防重点实验室仿造Samara制造了样机并且基于地磁场的方位定标，设计并完成了该类飞行器的操纵方案 [8]，但是没有提出明确的Samara的控制机理。

目前，国内外对于Samara飞行器的研究较少，控制方案尚未成熟。Samara的控制依赖于独立的视觉跟踪系统，该系统无法机载而且价格昂贵，决定了Samara目前的研究还是停留在了实验室的阶段，这严重限制了Samara在工程和民用上的应用前景。Samara飞行器没有固定的机头，运动时整个机身都处于旋转的状态，这给飞行器位置和姿态的测量以及飞行控制都带来巨大的挑战。并且Samara飞行器的控制机构仅有机翼尾部的螺旋桨电机和机翼后缘的副翼，如何在欠驱动下实现飞行器的轨迹控制也是一大难点。

在该背景下，本文作者所在的课题组在摒弃了Samara昂贵的视觉传感系统，采用普通民用的传感器和飞控板的条件下，设计了一款类Samara飞行器，并给出了该飞行器沿水平面直线飞行的控制方案，实现了平面直线跟踪控制。本文在课题组已有工作的基础上，研究曲线跟踪问题，给出了曲线跟踪控制律。仿真结果表明，所设计的跟踪控制律能够使类Samara飞行器以较高的精度跟踪预设轨迹曲线。

2. 问题描述与预备知识

2.1. 问题描述

以洛克希德·马丁公司的Samara为蓝本，本课题组自行设计并制造了一款类Samara飞行器(如图1)。该飞行器由机身、机身前端的螺旋桨电机、机翼和机翼后缘的副翼共同组成。机身长30 cm，由轻质铝板材料组成，上面集成了航空电池、飞控板、舵机、电机和部分姿态传感设备。机翼由轻木材料构成，翼展30 cm，平均弦长18 cm，机身和机翼通过碳棒连接。飞控板选用的是商用飞控pixhawk，在飞控板中集成了三轴陀螺仪、三轴加速度计和磁力计、气压计等普通民用传感器，摒弃了视觉传感器。

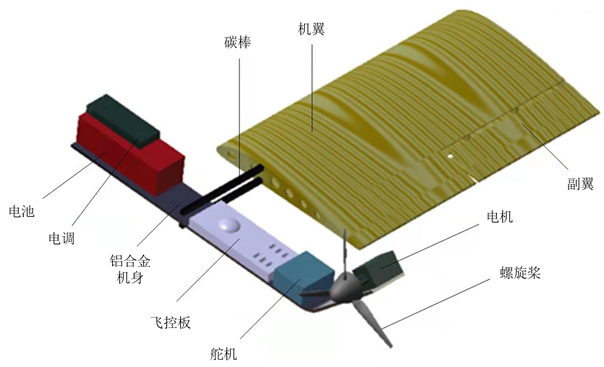
Figure 1. Samara-like aircraft design concept

图1. 类Samara飞行器设计概念图

如图1所示，飞行器的控制机构有两个，一是机身前端的螺旋桨电机，通过电机旋转产生推力，从而带动整个飞行器旋转来产生向上的升力，带动飞行器升空。二是机翼后缘的副翼，主要起到方向控制的作用。飞行器只有两个控制量，是典型的欠驱动系统，在对飞行器的飞行轨迹进行控制时，仅能够保证两个方向上的跟踪。所以在研究飞行器对曲线跟踪的问题时，主要考虑的是位于竖直平面的曲线的跟踪问题。其次，所使用的pixhawk飞控板所集成的姿态传感器在偏航角速度的测量上存在一定的限制，测量的最大偏航角速度不能超过35 rad/s，这限制了我们所能选用的螺旋桨电机的功率，从而影响了飞行器整机的转速。

本文所研究的内容为，针对类Samara飞行器无固定机头且结构不对称的难点，提出一种基于控制的建模方案，使模型更能符合类Samara飞行器本体自旋的特点。在曲线跟踪控制时，控制器选用的是线性自抗扰控制器(Linear Active Disturbance Rejection Control, LADRC)，使用LADRC来补偿建模时的误差以及消除电机通道和副翼通道的耦合。最后通过控制器使飞行器能够闭环跟踪上预设的曲线。下面对LADRC控制器进行简述。

2.2. LADRC控制器

自抗扰控制(Active Disturbance Rejection Control, ADRC)是韩京清研究员提出的一种非线性控制方法 [9]，它的核心思想就是将系统的不确定性以及各种扰动视为总扰动，以扩张状态观测器为手段，实时地对总扰动进行估计，并加以消除，从而把系统还原为标准的积分串联型，使得控制系统的设计从复杂到简单 [10] [11]。但是ADRC需要调节的参数过多，在实际工程应用上难以简单快速的控制目标。高志强博士在此基础上提出了线性自抗扰控制(LADRC)，并且将需要整定的参数大大减少，极大的促进了其在工程上的应用 [12]。

LADRC具有几乎模型无关的特点和天然的解耦性 [13]。使用LADRC控制器能够补偿类Samara飞行器建模时的误差，并且还能消除螺旋桨电机通道和副翼通道的耦合。

考虑以下二阶系统，被控对象：

$\ddot{y}=-a_1\stackrel{\dot{}}{y}-a_{2}y+bu+\omega$ (1)

式中，y、u分别是输出和输入， $\omega$ 为扰动。 $a_1$ 、 $a_0$ 以及 $\omega$ 均未知，b部分已知(将已知部分记为 $b_0$ )，则式(1)可以写为

$\ddot{y}=-a_1\stackrel{\dot{}}{y}-a_{2}y+\left(b-b_0\right)u+\omega +b_{0}u=f+b_{0}u$ (2)

其中， $f=-a_1\stackrel{\dot{}}{y}-a_{2}y+\left(b-b_0\right)u+\omega$ 为包含了外扰和内扰的总扰动。

选择状态变量： $x_1=y$， $x_2=\stackrel{\dot{}}{y}$， $x_3=f$，则 $x={\left[y\stackrel{\dot{}}{y}f\right]}^{\text{T}}$ 为包括了扰动的扩张状态，式(2)转化为

扩张状态空间描述：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=x_3+b_{0}u\\ {\stackrel{\dot{}}{x}}_3=\stackrel{\dot{}}{f}\\ y=x_1\end{array}$ (3)

对应的线性扩张状态观测器(LESO)为

$\{\begin{array}{l}{\stackrel{\dot{}}{\hat{x}}}_1={\beta }_1\left(y-{\hat{x}}_1\right)+{\hat{x}}_2\\ {\stackrel{\dot{}}{\hat{x}}}_2={\beta }_2\left(y-{\hat{x}}_1\right)+{\hat{x}}_3+b_{0}u\\ {\stackrel{\dot{}}{\hat{x}}}_3={\beta }_3\left(y-{\hat{x}}_1\right)\end{array}$ (4)

其中 ${\beta }_1$， ${\beta }_2$， ${\beta }_3$ 是待调参数。以LESO输出构成控制器

$u=\frac{1}{b_0}\left[l_2\left(r-{\hat{x}}_1\right)-l_1{\hat{x}}_2-{\hat{x}}_3\right]$ (5)

其中系数 $l_1$， $l_2$ 待定。被控对象(2)、LESO (4)和控制器(5)就共同组成了二阶LADRC。

使用高志强博士提出的“带宽法”，用控制器带宽 ${\omega }_c$ 和观测器带宽 ${\omega }_0$ 来代替上面的待定参数，得到：

${\beta }_1=3{\omega }_0,{\beta }_2=3{\omega }_0^2,{\beta }_3={\omega }_0^3$ (6)

$l_1=2{\omega }_c,l_2={\omega }_c^2$ (7)

经过上面的分析，LADRC需要调整的参数仅剩下 ${\omega }_0,{\omega }_c,b_0$ 三个，使得工程整定工作量大幅度减小。对大部分对象，在参数整定时， ${\omega }_0$ 与 ${\omega }_c$ 的关系可以在一定范围内固定，令

${\omega }_0\approx \left(3~5\right){\omega }_c$ (8)

3. 基于控制的建模

对于常规飞行器的建模，可以将飞行器的运动抽象为六自由度的刚体运动。但是由于类Samara飞行器本身结构的不对称性以及在飞行过程中本体自旋，无固定机头的特点，使用常规的建模方法，会给控制带来很大的困难。所以针对飞行器本体自旋的特点，提出一种基于控制的建模方案，使得新的模型更能表征类Samara飞行器的运动状态。

考虑到类Samara飞行器在飞行时产生升力的主要部件为机翼，机体产生的升力和阻力都要远远小于机翼，故在建模时进行简化，将机身抽象为一个质点，将飞行器的运动简化为飞行器质心的平动和机翼翼尖产生的挥舞运动两个运动的叠加，如图2(a)所示。其中， $F_L$ 是机翼旋转产生的等效升力， $\beta$ 是机翼与水平面的瞬时夹角(即挥舞角)， $F_D$ 是空气阻力，mg是重力，V表示飞行方向。将 $F_L$ 与竖直方向的夹角定义为 $\theta$， $F_L$ 在水平面的投影与正东方向的夹角定义为 $\phi$， $F_L$ 的方向可由 $\theta$ 和 $\phi$ 共同确定；xyz坐标系采用东北天坐标系，如图2(b)所示。

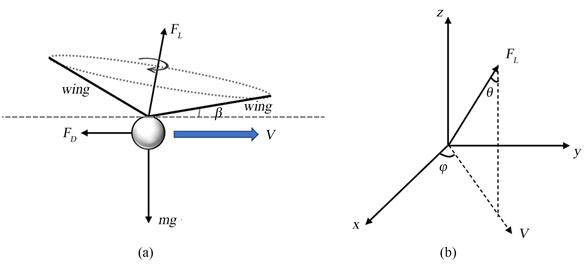
Figure 2. Samara-like equivalent flight diagram

图2. 类Samara飞行器等效飞行图

可得，质心的平动方程为：

$\left[\begin{array}{c}\stackrel{\dot{}}{u}\\ \stackrel{\dot{}}{v}\\ \stackrel{\dot{}}{w}\end{array}\right]=\frac{1}{m}\left[\begin{array}{c}{F}_L\sin \theta \cos \phi -k_{d}u\\ F_L\sin \theta \sin \phi -k_{d}v\\ F_L\cos \theta -mg-k_{d}w\end{array}\right]$ (9)

$\left[\begin{array}{c}\stackrel{\dot{}}{x}\\ \stackrel{\dot{}}{y}\\ \stackrel{\dot{}}{z}\end{array}\right]=\left[\begin{array}{c}u\\ v\\ w\end{array}\right]$ (10)

方程中 $u,v,w$ 为三轴线速度， $x,y,z$ 为三轴位移， $k_d$ 为阻力系数。 $F_L$ 的大小计算基于叶素理论 [14]：

$F_L=\frac{1}{2}{C}_l\rho S_{sa}{\Omega }^2$ (11)

其中， $C_l$ 为升力系数， $\rho$ 为空气密度， $S_{sa}$ 为机翼面积， $\Omega$ 为机体转速。

接着探讨飞行器的挥舞运动。借鉴直升机机翼挥舞运动的描述 [15]，类Samara飞行器机翼的挥舞运动满足以下方程：

$\ddot{\beta }+\frac{r_l\Omega }{8}\stackrel{\dot{}}{\beta }+{\Omega }^2\beta ={\Omega }^2\left({\beta }_0+K\ast {\delta }_e\right)$ (12)

其中， $r_l$ 为无量纲常数， ${\beta }_0$ 为机翼的锥度角， ${\delta }_e$ 为副翼舵角，K为增益系数。

该挥舞方程具有如下形式的准静态解 [16]：

$\beta \left(\psi \right)={\beta }_0-{\beta }_{1c}\cos \left(\psi \right)-{\beta }_{1s}\sin \left(\psi \right)$ (13)

$\stackrel{\dot{}}{\psi }=\Omega$ (14)

其中， $\psi$ 为偏航角，代表飞行器机身整体旋转的角度。 ${\beta }_{1c}$ 和 ${\beta }_{1s}$ 可以通过在每个周期中测量此时的挥舞角 $\beta$ 和偏航角 $\psi$ 得到。

通过 ${\beta }_{1c}$ 和 ${\beta }_{1s}$ 可以计算得到(9)式中的 $\phi$ 和 $\theta$，以此来确定升力 $F_L$ 的方向，如式(15)和(16)所示。

$\phi =\{\begin{array}{l}\arctan \left(\frac{{\beta }_{1s}}{{\beta }_{1c}}\right),{\beta }_{1c}>0\text{and}{\beta }_{1s}\ne 0\\ \pi +\arctan \left(\frac{{\beta }_{1s}}{{\beta }_{1c}}\right),{\beta }_{1c}<0\text{and}{\beta }_{1s}\ne 0\\ 0,{\beta }_{1c}>0\text{and}{\beta }_{1s}=0\\ \frac{\pi }{2},{\beta }_{1c}=0\text{and}{\beta }_{1s}>0\\ \pi ,{\beta }_{1c}<0\text{and}{\beta }_{1s}=0\\ \frac{3\pi }{2},{\beta }_{1c}=0\text{and}{\beta }_{1s}<0\end{array}$ (15)

$\theta =\sqrt{{\beta }_{1s}^2+{\beta }_{1c}^2}$ (16)

将式(16)代入式(14)，可将挥舞运动表征为 $\theta$ 和 $\phi$ 的方程：

$\beta \left(\psi \right)={\beta }_0-\theta \cos \left(\psi -\phi \right)$ (17)

最后考虑机身头部螺旋桨电机转速n与机身转速 $\Omega$ 之间的关系，由动量矩定理可得飞行器旋转的动态方程：

$\stackrel{\dot{}}{\Omega }=\frac{k_1{R}_1}{J}{n}^2-\frac{k_2{R}_2}{J}{\Omega }^2$ (18)

其中，J为机体的转动惯量， $R_1$ 、 $R_2$ 分别为动力臂和阻力臂长度， $k_1$ 、 $k_2$ 为常系数。

综上所述，飞行器的整体建模如式(19)所示。

$\{\begin{array}{l}\stackrel{\dot{}}{u}=\frac{1}{m}\left(F_L\sin \theta \cos \phi -k_{d}u\right)\\ \stackrel{\dot{}}{v}=\frac{1}{m}\left(F_L\sin \theta \sin \phi -k_{d}v\right)\\ \stackrel{\dot{}}{w}=\frac{1}{m}\left(F_L\cos \theta -mg-k_{d}w\right)\\ \stackrel{\dot{}}{x}=u\\ \stackrel{\dot{}}{y}=v\\ \stackrel{\dot{}}{z}=w\\ \ddot{\beta }+\frac{r_l\Omega }{8}\stackrel{\dot{}}{\beta }+{\Omega }^2\beta ={\Omega }^2\left({\beta }_0+K\ast {\delta }_e\right)\\ \stackrel{\dot{}}{\psi }=\Omega \\ \stackrel{\dot{}}{\Omega }=\frac{k_1{R}_1}{J}{n}^2-\frac{k_2{R}_2}{J}{\Omega }^2\end{array}$ (19)

4. 曲线跟踪的控制方案

由于类Samara飞行器的控制机构仅有机身上的螺旋桨电机和机翼上的副翼，仅能保证两个方向上的控制和跟踪。所以本文所研究的曲线跟踪问题，需要将曲线限制在某一竖直平面内。以飞行器前进方向为x'轴设定一个轨迹坐标系，该坐标系和惯性坐标系具有同一个z轴，x'轴和x轴之间存在一个夹角 $\phi$，即上文所描述的方向角，如图3所示。

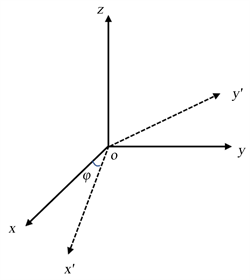
Figure 3. Schematic diagram of the relationship between the coordinate system

图3. 坐标系关系示意图

所跟踪的曲线位于 $x^{\prime }oz$ 平面内，该平面方程如下：

$\tan \left(\phi \right)x-y=0$ (20)

在 $x^{\prime }oz$ 平面内构建所需要跟踪的曲线 $z=f\left(x^{\prime }\right)$，实际的坐标可以由式(20)的平面方程解出：

$\{\begin{array}{c}\begin{array}{l}x=x^{\prime }\cos \phi \\ y=x^{\prime }\sin \phi \end{array}\end{array}$ (21)

构建好曲线后，为了使飞行器跟踪上预设的曲线，采取的控制方案包括两点。一是飞行高度控制，保持每一时刻飞行器在竖直方向上能够跟踪上预设的曲线。二是飞行方向控制，保持每一时刻飞行器所受到的合力方向始终与曲线的切线方向保持一致。当同时完成了高度跟踪和飞行方向跟踪，就能够保证飞行器能够时刻跟踪上预设的曲线，如图4所示，定义曲线切线和x'轴的夹角为航迹倾角 $\alpha$。

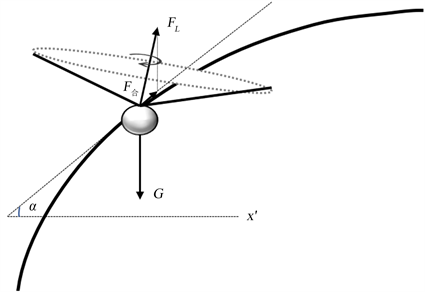
Figure 4. Schematic diagram of Samara-like aircraft curve tracking

图4. 类Samara飞行器曲线跟踪示意图

由于高度控制通道和飞行方向控制通道在控制时会存在一定的耦合，所以选用上文提到的LADRC控制器来消除纵向和横侧向通道的耦合，具体的控制流程如图5所示。

Figure 5. Control scheme flow chart

图5. 控制方案流程图

设预设的平面曲线为 $z=f\left(x^{\prime }\right)$，它是连续可微且位于 $x^{\prime }oz$ 平面内。此时飞行器所在点为 $P\left({x^{\prime }}_0,z_0\right)$，则当前目标高度为：

$h_{ref}=f\left({x^{\prime }}_0\right)$ (22)

当前的航迹倾角为：

$\alpha =\arctan \left(f^{\prime }\left({x^{\prime }}_0\right)\right)$ (23)

通过航迹倾角 $\alpha$ 可以计算期望的挥舞角信号 ${\beta }_{ref}$。计算的流程如下：

将图4所示的飞行器跟踪预设曲线的过程抽象化，从而得到图6的受力分析图。

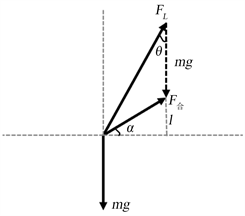
Figure 6. Curve tracking force diagram

图6. 曲线跟踪受力示意图

如图6，当前的航迹倾角 $\alpha$ 决定了期望的合力方向，所以问题转化为已知期望合力方向和升力 $F_L$ 的大小，求期望的升力 $F_L$ 方向的问题。下面展示升力 $F_L$ 方向的求解过程：

${\left(mg+l\right)}^2+{\left(\frac{l}{\tan \alpha }\right)}^2=F_L^2$ (24)

展开后，得

$\frac{{\tan }^2\alpha +1}{{\tan }^2\alpha }{l}^2+2mgl+{\left(mg\right)}^2-F_L^2=0$ (25)

由求根公式，在 $l>0$ 且 $F_L>mg$ 的前提下，可得方程有唯一解

$l=\frac{-b+\sqrt{b^2-4ac}}{2a},a=\frac{{\tan }^2\alpha +1}{{\tan }^2\alpha },b=2mg,c={\left(mg\right)}^2-F_L^2$ (26)

从而可以计算出，此时升力和竖直方向的夹角：

${\theta }_{ref}=\arccos \left(\frac{mg+l}{F_L}\right)$ (27)

参考式(17)可以得到，期望的挥舞角信号为：

${\beta }_{ref}={\beta }_0-{\theta }_{ref}\cos \psi$ (28)

控制方案的流程为通过此时飞行器所在位置的x坐标和预设曲线解析式 $z=f\left(x^{\prime }\right)$ 即可计算出目标高度 $h_{ref}$ 和期望的挥舞角信号 ${\beta }_{ref}$，再利用LADRC对高度和挥舞角信号的误差进行控制，则可实现对曲线的跟踪。

在以上论述的控制方法下，类Samara飞行器在理论上能够完成对任意曲线的跟踪。但是由于本课题组设计并制造的类Samara飞行器所使用的传感器对偏航角速度有量程的限制(不超过35 rad/s)，这限制了飞行器自身的旋转角速度 $\Omega$，从而也限制了所能产生的最大的升力大小。接下来讨论实际所能跟踪的曲线要求：

假设飞行器此时所在的位置为点A，该点曲线的斜率为 $k_1$，飞行器横向速度为 $u_1$，纵向速度为 $w_1$。假设此时飞行器仍然能跟踪上预设曲线，则有

$\frac{w_1}{u_1}=k_1$ (29)

经过时间∆t后，飞行器来到点B，假设在B点也满足跟踪上曲线的要求，该点曲线的斜率为 $k_2$，飞行器横向速度为 $u_2$，纵向速度为 $w_2$。则有

$\frac{w_2}{u_2}=k_2$ (30)

由于飞行器具有最大升力限制 $F_{L_{\max }}$，所以理论上，纵向所能达到的最高加速度为

$a=\frac{F_{L_{\max }}-mg}{m}$ (31)

考虑到需要跟踪上对应的预设曲线，有

$w_1+a\Delta t>w_2$ (32)

又由于控制策略是控制合力的方向始终保持与切线方向一致，所以理论上横向和纵向都是变加速度运动，即 $w_1$ 随着时间的增加而增大， $u_1$ 也随着时间的增加而增大，所以有 $w_2>w_1$ 且 $u_2>u_1$ 恒成立。式(32)代入式(29)和(30)得到

$a\Delta t>k_2{u}_2-k_1{u}_1>k_2{u}_1-k_1{u}_1=\left(k_2-k_1\right)u_1$ (33)

通过分析式(33)我们可以知道，飞行器在所设定的控制策略之下，能够实现曲线的跟踪，需要满足的条件有两个，一是曲线的斜率在短时间内不能有太大的变化，二是沿着曲线横向的飞行速度不能过快。

综上所述，本文是采用高度控制和挥舞角控制的双通道控制来控制类Samara飞行器的纵向以及横侧向的运动，在满足要求的情况下，飞行器能够沿着预设的曲线进行飞行。在所提出的理论的指导下，还需要通过仿真来验证控制方法的有效性。

5. 仿真验证

使用matlab的simulink仿真工具对所提出的控制方法进行验证。先搭架实验所需的模块，主要包括预设曲线设计模块、航迹倾角和目标高度计算模块、目标挥舞角计算模块、控制器模块、传感器模块和Samara飞行器建模模块。然后将各模块进行相应的连接，组成我们的验证平台。

其中，高度控制和挥舞角控制模块均采用LADRC控制器。高度控制所选择的控制参数如下：

$\{\begin{array}{l}{b}_0=18\\ {\omega }_c=6\\ {\omega }_0=20\end{array}$ (34)

挥舞角控制所选择的控制参数如下：

$\{\begin{array}{l}{b}_0=353.4\\ {\omega }_c=70\\ {\omega }_0=300\end{array}$ (35)

对预设曲线进行规划。假设飞行任务需要飞行器经过以下点，(0, 0)，(1, 1)，(2, 1.5)，(3, 1.8)，(4, 2)，(5, 2.1)。利用matlab的polyfit函数对这些点进行三阶多项式曲线拟合，得到曲线方程为：

$z=0.0213x^3-0.2615x^2+1.1950x+0.0111$ (36)

通过曲线解析式，可以计算得到目标高度 $h_{ref}$ 和期望的挥舞角信号 ${\beta }_{ref}$ 如图7所示：

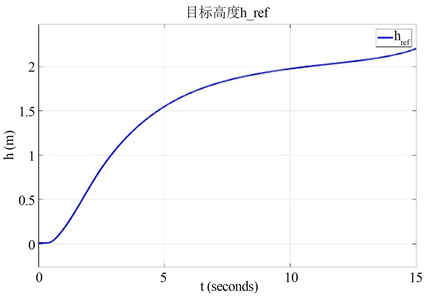
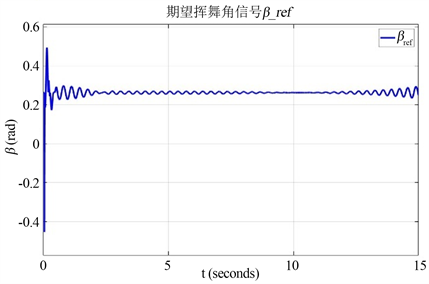
Figure 7. Target height and desired swing angle signal

图7. 目标高度和期望的挥舞角信号

将该曲线方程输入预设曲线模块，进行曲线跟踪。跟踪的效果如下所图所示：

Figure 8. Height tracking renderings

图8. 高度跟踪效果图

图8为高度跟踪的效果曲线，虚线表示计算出的目标高度 $h_{ref}$，实线表示此时飞行器的实际高度。可以看出，实际的跟踪效果是非常不错的，高度跟踪能够跟踪上，说明飞行器在每一时刻都在预设的曲线上进行飞行。

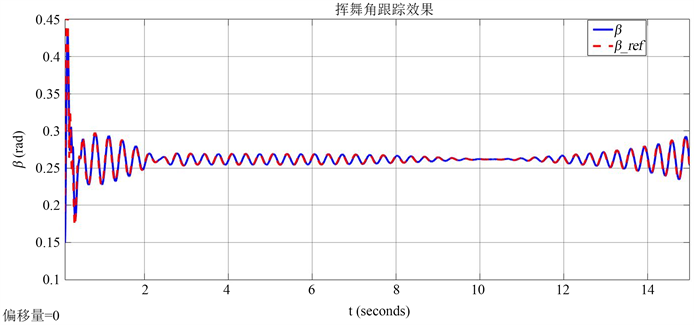
Figure 9. Swing angle tracking renderings

图9. 挥舞角跟踪效果图

图9为挥舞角跟踪的效果曲线，通过上面的分析可以知道，挥舞角的跟踪效果决定了飞行器的飞行方向的跟踪效果。从结果上来说，挥舞角的跟踪效果达到了预期的目标，这也就决定了飞行器在每一时刻的飞行方向都是沿着曲线的切线方向。

Figure 10. Curve tracking effect

图10. 曲线跟踪效果

图10为最终的曲线跟踪效果，从图中可以看出在开始的时间实际曲线和预设曲线之间还存在一定的误差，这是螺旋桨电机的转速跟踪需要有一定的调节时间导致的，随着时间的逐渐增加，实际曲线和预设曲线的误差逐渐减小，很好地实现了曲线跟踪的目标。

6. 结论

本文介绍了以洛克希德·马丁公司研发的Samara飞行器为蓝本，本课题组自行设计并制造了一款使用普通民用传感器的类Samara飞行器。针对类Samara飞行器的曲线跟踪问题，提出了一种基于控制的建模方案，给出了曲线跟踪控制律。仿真结果表明，所设计的跟踪控制律能够使类Samara飞行器以较高的精度跟踪预设轨迹曲线，验证了本文的建模方式以及控制方案的有效性。

NOTES

^*通讯作者。