1. 引言
增材制造技术历经近三十年日新月异的发展,已从概念模型快速成型发展到了覆盖产品设计、研发和制造的全部环节,并随着材料成本进一步降低在不久的将来成为个性化定制产品制造的重要途径 [1]。不同于减材制造或通过模具加工制造,相关产品的质量和精度已有成熟的控制和检测方式,增材制造通过3D打印的方式,极易造成产品精度不高、可控性差等问题 [2]。那么如何通过无接触的方式实施实时的精度检测并将检测结果反馈至3D打印机,修正打印输出,实现高精度的增材制造过程?
新近发展的高精度三维扫描成像技术将有助于上述问题的解决。它利用特定的光源和摄像技术完成不同角度下的图像数据采集,并结合一定的图像处理算法,实现三维物体的高精度还原。尽管该技术已广泛应用于逆向工程领域并取得了非常好的成效,不同于逆向工程中没有时效性要求,本研究针对的研究对象具有较高的实时性要求,需要边3D打印边实时还原已打印部分并与原设计图进行对比,调整误差部分,不断提高后续打印精度,实现最终的高质量打印。
目前,三维扫描主要包括以下步骤:三维点云采集、点云去噪、点云数据配准等过程 [3],其中三维点云采集和去噪过程相对较快,而点云的数据配准过程却异常复杂,占据整个逆向过程最大部分时间消耗。与此同时,数据配准的精度也直接决定了最终三维图像的还原质量,因此如何实现快速、准确地三维点云数据配准是解决上述问题的关键。
2. 国内外点云配准算法研究的现状
国内外关于点云配准算法的研究已做了大量的工作,按照算法的特点对其进行分类,如图1所示。大的来说,根据点云数据的获取来源分为“同源配准”和“跨源配准”。同源点云的配准是指从同一类型的传感器,但在不同的时间或视角下获取的点云。同源配准可以进一步分为基于优化的配准方法、基于特征学习方法、基于端到端学习方法。
(一) 基于优化的配准方法
基于优化的配准是利用优化策略估计变换矩阵,如迭代最近点算法(Iterative Closest Point, ICP)。大多数基于优化的配准方法 [4] [5] [6] [7] 包含两个阶段:对应点搜索和变换估计。对应点搜索是在另一个点云中找到每个点的匹配点。变换估计就是利用对应关系来估计变换矩阵。这两个阶段将进行迭代,以找到最佳的变换。在迭代过程中,初始的对应可能并不准确。随着不断的迭代,对应关系将变得越来越精确。然后,利用精确的对应关系,使估计的变换矩阵变得精确。通过比较点的坐标差或特征差,可以找到对应关系。这一类的优点有两个:
1) 严密的数学理论可以保证它们的收敛性。
2) 它们不需要训练数据,可以很好地推广到未知场景。
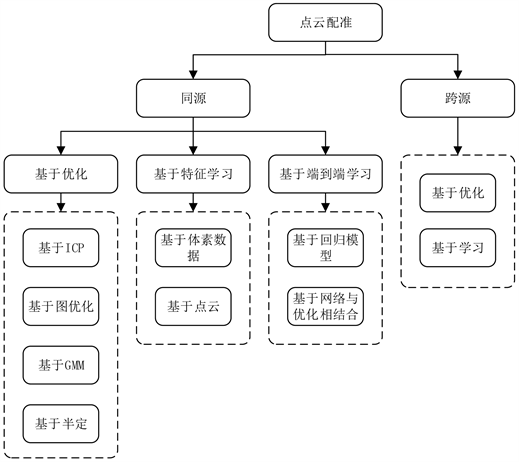
Figure 1. Classification of point cloud registration
图1. 点云配准分类
这一类的局限性在于,需要许多复杂的策略来克服噪声、异常值、密度变化和部分重叠的变化,这将增加计算成本。
(二) 特征学习的配准方法
特征学习的配准方法不同于经典的基于优化的配准方法,特征学习方法 [8] [9] [10] 采用深度神经网络来学习鲁棒的特征对应搜索。这种方法的优点在于可以提供鲁棒、准确的对应搜索,通过简单的RANSAC方法,精确的对应可以得到准确的配准结果。而这种方法的局限性在于需要大量的训练数据,并且在未知场景中,如果场景与训练数据存在较大的分布差异,则配准性能会急剧下降。
(三) 基于端到端学习的方法
利用端到端神经网络解决配准问题。该方案的输入是两帧点云,输出是对齐这两点云的变换矩阵。端到端学习方法的基本思想是将配准问题转化为回归问题。该方法将深度学习与传统的Lucas-Kanade优化方法相结合,是特征度量配准的一项开创性工作。这一类的优点有两个方面:
1) 神经网络专门针对配准任务进行设计和优化。
2) 它既可以利用传统数学理论的优点,又能利用深层神经网络的优点。
现有方法的局限性有两个方面:
1) 回归方法将变换参数估计看作黑匣子,距离度量在基于坐标的欧氏空间中进行测量,该空间对噪声和密度差敏感。
2) 特征度量配准方法考虑了局部结构信息,这对配准非常重要。
(四) 跨源点云配准方法
跨源点云配准是对不同类型传感器(如Kinect和Lidar)的点云进行配准。根据文献 [11] [12],跨源点云配准由于噪声和离群点、密度差、部分重叠和尺度差等因素的综合作用而更具挑战性。一些算法 [12] [13] [14] [15] [16] 使用复杂的优化策略,通过克服跨源挑战来解决跨源点云配准问题。例如,CSGM [12] 将配准问题转化为图匹配问题,并利用图匹配理论来克服这些挑战。最近,FMR [13] 展示了使用深度学习对齐跨源点云的性能。这些方法都试图利用优化策略或深层次的神经网络来克服交叉源的挑战来估计变换矩阵。跨源点云配准的优点是结合多个传感器的优点,为增强现实、建筑施工等计算机视觉任务提供全面的三维视觉信息。然而,现有的配准方法存在精度低、时间复杂度高等缺陷,尚处于起步阶段。
3. 现有国内外点云配准算法的不足
1) 现有的三维点云数据采集技术普遍采用结构光,其精度有限。
根据三维光学扫描原理,可分为基于三维激光扫描、基于结构光扫描以及基于飞行时间扫描。目前基于迭代最近点三维点云配准算法研究普遍采用结构光采集点云数据,尽管该方式已普遍应用,也十分方便,但精度相对有限,不够满足对精度要求苛刻的场景。
2) 现有的三维点云粗配准算法缺乏准确性,不适用于本文研究对象。
现有的粗配准方案,如PFH、FPFH、3Dsc、NDT,不仅准确度不够,还比较费时,最高需要40秒,最低也需要1秒多,显然这样的时耗是不可容忍的。此外前述的方案也是不适合基于旋转盘的三维扫描系统。
3) 现有高精度的三维点云配准算法过于费时,达不到本项目的要求。
4. 基于迭代最近点的三维点云配准改进方案
针对现有研究的不足,笔者拟从三维点云数据的高精度采集入手,结合传统的基于迭代最近点的三维点云配准算法,通过多图扫描固定结构的参照物获取点云配准的旋转矩阵和平移参数,并以此作为迭代最近点配准算法的初始参数,实现对目标物体三维点云数据的快速、高精度配准。具体三维点云配准改进方案如图2,内容包括:
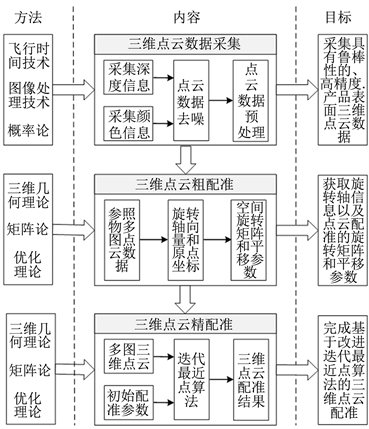
Figure 2. Improved scheme of 3D point cloud registration based on iterative closest point
图2. 基于迭代最近点的三维点云配准改进方案
1) 基于飞行时间的三维点云数据采集研究
针对三维光学仪器中基于结构光的三维扫描技术精度有限的问题,研究利用基于飞行时间(Time of Flight, ToF)技术从复杂的工业产品结构中采集出具有鲁棒性的产品表面三维点云数据,并将所采集的原始数据做“去噪”(Denoising)和“去边”(Outlier)处理,为后续算法研究与验证奠定基础。
2) 基于参照物的三维点云粗配准算法研究
针对现有研究中粗配准算法不适用以及基于迭代最近点三维点云配准算法的初始参数设置困难问题,研究利用L型或立方体参照物,以固定的旋转角度扫描获取参照物的点云数据,实施已知参照物的三维点云配准,获取点云配准的旋转矩阵和平移参数,并以此作为后续待逆向物体点云配准的初始参数,实现较为有效和“精准”的粗配准。
3) 基于改进迭代最近点的三维点云精配准算法研究
针对基于传统的迭代最近点的三维点云配准算法复杂度高、运算量大等问题,研究利用前述基于参照物的粗配准结果精确实施多图点云的初始配准过程,快速找出相邻点云重叠区域并实施区域分割,完成重叠区域的基于迭代最近点算法的配准,最终获得较高精度的三维配准结果。
5. 基于迭代最近点的三维点云配准算法改进
根据上述方案,笔者首先研究基于Kinect V2的高精度三维点云数据的采集方法;随后采用该采集方法获取参照物的多图三维点云数据,并据此计算出转换矩阵和平移参数作为粗配准参数;最后在上述的基础上,研究基于迭代最近点算法的三维点云配准。具体为:
(一) 基于Kinect V2的三维点云数据的采集
鉴于Kinect V2深度传感器具有通过飞行时间技术获取深度信息能力,拟采用该系统作为点云数据采集平台,该平台硬件包含颜色摄像机、深度传感器、红外发射器以及一组麦克风,满足本研究对于点云采集的精度需求。基于飞行时间技术的基本原理如图3所示。
由于设备或者测量环境的影响,所采集的深度图通常包含有噪声,相关噪声若不及时处理则会影响数据的精度。深度值在一定的区域范围通常是连续的,因此将突变的值看成噪声并加以剔除。经过去噪后还需对数据开展预处理。其处理过程从数学上可以表达为:
(1)
其中,
为原始数据,
为加权系数,
为像素点领域。对于双边滤波而言,其加权系数包含空域权重和图像灰度域权重,即
,对应有:
(2)
(3)
最终得到的深度数据和颜色信息就可以作为三维点云数据。
(二) 基于参照物的三维点云粗配准参数的获取
为了使得粗配准算法简单而又有效,拟采用L型或立方体物体作为参照物(如图4所示),其共同特点是结构简单,且能做到与旋转盘平面垂直。
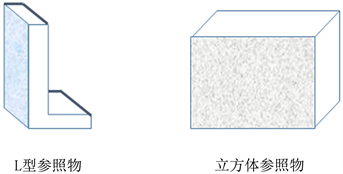
Figure 4. Structure of the reference object
图4. 参照物结构
基于多图点云,任意的三维平面图可以表达为:
(4)
给定任意两个空间平面,并假设旋转过程中空间平面与旋转轴平行。
(5)
其相交线
与旋转轴平行,因此只要确定了旋转轴的原点和旋转角度,则相应的变换矩阵便可得。
(三) 基于改进迭代最近点的三维点云精配准的实现
点云配准问题可以描述为如下数学问题:
(6)
这里
和
分别表示源点云和目标点云。基于迭代最近点算法整体上看可以将点云配准问题分解成两个问题:找最近点和找最优变换。
找最近对应点:利用前述得到的变换矩阵和平移参数作为初始
和
(之后采用上一次迭代得到的
和
)对点云做初始变换,得到一个临时的变换点云,然后用这个点云和目标点云进行比较,找出源点云中每一个点在目标点云中的最近邻点。由于采用了参照物,因此这一步相较传统算法有较大的效率提升。
求解最优变换:分别求出源点云和目标点云的质心
,
,相对质心重新建立点云坐标,令
和
,得到矩阵
,最后对H矩阵作奇异值(SVD)分解,
,最终便可以得到,
和
。
之后,对上述两步做迭代处理,直至结果满足一定的条件。
6. 算法仿真
算法的仿真基于Matlab,并以经典的“兔子”点云配准过程(如图5所示)为例,下表1为本文提出的改进ICP算法与经典ICP算法之间的配准平均时长对比,在同样10,000点左右的数据,经典的ICP算法平均需要5.45秒,而改进的ICP算法由于减少了原始数据的错误引入,以及实施了相对较为精确的粗配准,使得ICP算法不那么盲目,结果仅需0.21秒。如此快速的配准非常适应于增材制造过程中的实时调整。

Figure 5. The process of point cloud registration
图5. 点云配准过程

Table 1. Comparison of average duration
表1. 平均时长对比
7. 结论
基于迭代最近点的三维点云配准改进算法,利用飞行时间技术提高原始三维点云数据采集精度,减少源头数据误差引入,通过辅助的参照物多图扫描获取旋转轴信息及其转换矩阵,为目标物体的三维点云粗配准提供较好的初始信息,实现高精度、快速的目标物体的点云精配准,为高精度的增材制造过程提供算法支撑。
基金项目
本文系2021年浙江省教育厅一般科研项目课题——《基于迭代最近点的三维点云配准改进算法研究》(项目编号Y202147949)研究成果。