涨圈主密封面润滑状态判断及影响因素分析

Judgment of Lubrication State of Main Sealing Surface of Piston Ring and Analysis of Influencing Factors

摘要: 本文使用精确度较高的JFO空化模型，通过求解雷诺方程的边界条件和数值解，建立了液膜压力分布模型，研究了涨圈不同端面形貌对润滑状态和泄漏量的影响：端面锥度的存在会增大泄漏量，且正锥度的影响更大。波幅和波数都会造成泄漏，但同时可以提升液膜压力和承载力，因此在保证泄漏量的前提下可适当地提高波幅和波数；当表面粗糙度过大时，将导致产生较大流动压力的难度提升等结论。最后对操作参数进行了研究，结果表明：增大介质的压差会导致润滑条件变得恶劣，从而增大泄漏量；而增大介质的粘度和介质与旋转轴的转速则可以提升液膜的承载能力，有助于润滑的进行，降低泄漏量。

Abstract: In this paper, the JFO cavitation model with high accuracy is used to establish the pressure distribution model of liquid film by solving the boundary conditions and numerical solutions of Reynolds equation. Then, the influence of different surface topography on the lubrication state and leakage is studied, and the existence of the end taper will increase the leakage, and the positive taper has a greater impact. Both wave amplitude and wave number can cause leakage, which can increase the pressure and bearing capacity of liquid film at the same time. Therefore, the wave amplitude and wave number can be appropriately increased on the premise of guaranteeing the  leakage rate. When the surface roughness is too large, it will lead to the difficulty of producing large flow pressure. Finally, the operating parameters are studied, and the results show that: increasing the pressure difference of the medium will lead to poor lubrication conditions, thus increasing the leakage amount; increasing the viscosity of the medium and the rotation speed of the medium and the rotating shaft can improve the bearing capacity of the liquid film, which is conducive to lubrication and reduce the leakage.

1. 前言

涨圈作为典型的机械密封结构，具有工作压力范围广、能够承受较高的线速度和使用温度范围大等特点 [1]，广泛应用于车辆、火箭和航空发动机以及涡轮增压器等轴封装置上。一般将涨圈密封与配油衬套凹槽内壁形成的密封面称为主密封面，主密封面主要受油液压力作用；由于自带的弹力效果，将涨圈密封的外表面与进油衬套内表面贴合形成的密封面称为第二密封面，如图1所示。国内外学者对涨圈的研究主要集中在密封环受力变形、温升及泄漏量等方面，如牛利民 [2] 等金属涨圈接触式密封设计实践，对航空机械中的涨圈使用要求、密封原理、设计特点、性能评价、材料选择和技术要求作了讨论；李涛 [3] 对涨圈型旋转密封装置及其性能进行了研究，主要对涨圈型旋转密封装置的性能进行了理论和试验研究，建立了泄漏量和密封间隙温升的数学模型，并进行仿真分析与试验结果进行对比。

随着涨圈在工作条件下的温度、压力和转速越来越高，导致密封面的润滑状态恶化，其端面与旋转轴凹槽面发生剧烈的摩擦和磨损，将引起涨圈热变形和厚度减薄，导致泄漏增大直至使失效。因此研究涨圈密封面的润滑状态及其影响因素，对于高性能涨圈设计具有重要的指导意义。

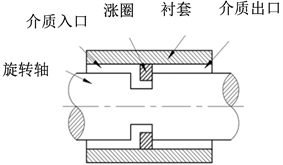
Figure 1. Physical drawing of expansion ring parts and its sealing diagram

图1. 涨圈零件实物图及其密封示意图

2. 涨圈润滑状态分析

润滑状态可以分为边界润滑、混合润滑和完全流体润滑。其中在边界润滑条件下，流体不提供承载力；在完全流体润滑状态下，流体提供全部的承载力；而在混合润滑状态下，流体产生的承载力与微凸体接触产生的承载力共同分担载荷 [4]。

如图2所示，p_F为衬套的反作用压力，其产生的摩擦力为F_f，作用在AB面上介质压力p₀产生的合力F_AB为闭合力，而作用在CD面上用于推开端面的力是开启力，它包括流体提供的开启力F_K1和微凸体提供的开启力F_K2，在稳态的情况下满足下式：

$F_{AB}-F_f=F_{K1}+F_{K2}$ (1)

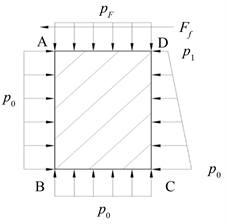
Figure 2. Stress diagram of expansion ring

图2. 涨圈受力示意图

当 $F_{AB}-F_f=F_K{}_1$ 时，流体提供全部的承载力，此时主密封面没有发生接触，涨圈处于完全流体润滑状态，而当 $F_{AB}-F_f>F_K{}_1$ 时，流体的承载力不能完全平衡闭合力，由微凸体承载力F_K2提供部分开启力，涨圈处于混合润滑状态。为了判断密封所处的润滑状态，必须计算主密封面的液膜承载力以及微凸体承载力。

对于大多数混合润滑状态，可以合理地假设流体在整个密封界面区域是连续的 [5]。液膜的形状主要与密封面的几何形状有关，液膜厚度可以用下式进行表示：

$h=h_0+h\left(r,\theta \right)$ (2)

式中： $h_0$ 为基础膜厚； $h\left(r,\theta \right)$ 为与端面几何形状有关的膜厚。

3. 液膜压力分布计算

3.1. 表面流体润滑控制方程

描述液膜压力分布的方程是雷诺方程，依据密封间隙内流体的流动特点，做如下假设：

1) 密封端面的流动介质为连续的牛顿流体，且为层流，忽略流体惯性效应；

2) 流体在涨圈端面与凹槽端面接触时没有相对滑动；

3) 流体液膜的厚度很小，因此液膜压力沿液膜厚度方向大小是一样的；

4) 与流体液膜相邻的固体表面曲率半径远大于液膜厚度，忽略液膜曲率影响。

5) 在稳态分析时忽略与时间相关的瞬态项根据上述假设，可以得到柱坐标下雷诺方程数学表达式 [6]：

$\frac{\partial }{\partial r}\left(\frac{\rho r{h}^3}{\mu }\frac{\partial p}{\partial r}\right)+\frac{1}{r}\frac{\partial }{\partial \theta }\left(\frac{\rho h^3}{\mu }\frac{\partial p}{\partial \theta }\right)=6\omega r\frac{\partial \left(\rho h\right)}{\partial \theta }$ (3)

式中： $\left(r,\theta \right)$ 为极坐标系的极半径与极角； $\mu$ 为密封介质的动力粘度； $\rho$ 为密封介质的密度；p为端面流体压力； $\omega$ 为旋转轴转速。

对于涨圈密封来说，沿周向液膜厚度发生变化，可能会产生空化现象。本文采用JFO空化模型 [7] [8]，这种模型由Jakobosson和Floberg、Olsson提出。JFO是考虑质量守恒定律而确定的，虽然计算较复杂，但是准确度最高。对于JFO空化模型，首先定义一个参数 $\lambda$，在完整的液膜区域，液膜的密度等于其实际的密度 ${\rho }_c$，而在空化区域密度为 $\rho$，则：

$\lambda =\frac{\rho }{{\rho }_c}$ (4)

在空化区，为液体于气体的混合区，密度比 $\lambda <1$，设置判别系数g等于0，压力等于空化压力，即：

$\lambda <1,g=0,p=p_c$ (5)

而在全液膜区域，将判别系数g等于1，则有：

$\lambda \ge 1,g=1,p=p_c+\beta \left(\lambda -1\right)$ (6)

3.2. 求解雷诺方程的边界条件

对于密封涨圈，其内外径处的压力是已知的，可以得到压力边界条件：

$\{\begin{array}{l}\lambda =\frac{p_1-p_c}{\beta },r=R_1\\ \lambda =\frac{p_2-p_c}{\beta },r=R_2\end{array}$ (7)

式中： $p_1$ 入口压力； $p_2$ 出口压力； $p_c$ 为空化压力。

选一个周期的扇形区域研究，并在边界上施加周期边界条件，而周期边界条件为：

$\lambda \left(r,\theta +\frac{2\pi }{N}\right)=\lambda \left(r,\theta \right)$ (8)

3.3. 雷诺方程的数值求解

涨圈密封计算区域为圆环形，可以取一块扇形区域进行求解。将计算区域按极坐标方向均匀的划分网格，如图3所示，网格尺寸为：

$\begin{array}{l}\Delta r=\frac{R_2-R_1}{m}\\ \Delta \theta =\frac{2\pi }{Nn}\end{array}$ (9)

式中：m，n是径向与周向划分的网格数；N为计算区域等分份数。

沿径向和周向给网格编号i,j，则网格上任何一点的位置可以用极坐标表示：

$\begin{array}{l}r\left(j\right)=R_1+\left(j-1\right)\Delta r\\ \theta \left(i\right)=\left(j-1\right)\Delta \theta \end{array}$ (10)

按照Lebeck提出的离散格式对方程离散 [9]，化简成下式：

${\lambda }_{i,j}=\frac{1}{D_{i,j}}\left(E_{i,j}{\lambda }_{i-1,j}+F_{i,j}{\lambda }_{i+1,j}+G_{i,j}{\lambda }_{i,j-1}+I_{i,j}{\lambda }_{i,j+1}+J_{i,j}\right)$ (11)

式中：

$\begin{array}{l}{D}_{i,j}=\frac{h_{i-1/2}^3\beta g_{i,j}}{12\mu r_{i,j}}\frac{\Delta r}{\Delta \theta }+\frac{h_{i+1/2}^3\beta g_{i,j}}{12\mu r_{i,j}}\frac{\Delta r}{\Delta \theta }+\frac{h_{i,j-1/2}^3\beta g_{i,j}}{12\mu }\left(r_{i,j}-\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}\\ +\frac{h_{i,j+1/2}^3\beta g_{i,j}}{12\mu }\left(r_{i,j}+\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}+r_{i,j}\omega \frac{h_{i,j}}{2}\left(1-g_{i,j}\right)\Delta r\\ E_{i,j}=\frac{h_{i-1/2}^3\beta g_{i-1,j}}{12\mu r_{i,j}}\frac{\Delta r}{\Delta \theta }+r_{i,j}\omega \frac{h_{i-1,j}}{2}\left(1-g_{i-1,j}\right)\Delta r\\ F_{i,j}=\frac{h_{i+1/2,j}^3\beta g_{i+1,j}}{12\mu r_{i,j}}\frac{\Delta r}{\Delta \theta }\\ G_{i,j}=\frac{h_{i,j-1/2}^3\beta g_{i,j-1}}{12\mu }\left(r_{i,j}-\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}\\ I_{i,j}=\frac{h_{i,j+1/2}^3\beta g_{i,j+1}}{12\mu }\left(r_{i,j}+\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}\\ J_{i,j}=r_{i,j}\omega \frac{1}{2}\Delta r\left(g_{i-1,j}{h}_{i-1,j}+\frac{1}{2}\left(g_{i,j}{g}_{i-1,j}\right)\left(h_{i,j}-h_{i-1,j}\right)-g_{i,j}{h}_{i,j}\right)\\ -\frac{1}{2}{g}_{i,j}{g}_{i+1,j}\left(h_{i+1,j}-h_{i,j}\right)r_{i,j}\omega \frac{1}{2}\Delta r+\frac{h_{i-1/2,j}^3\beta }{12\mu r_{i,j}}\left(g_{i,j}-g_{i-1,j}\right)\frac{\Delta r}{\Delta \theta }\\ +\frac{h_{i+1/2,j}^3\beta }{12\mu r_{i,j}}\left(g_{i,j}-g_{i+1,j}\right)\frac{\Delta r}{\Delta \theta }+\frac{h_{i,j-1/2}^3\beta }{12\mu }\left(g_{i,j}-g_{i,j-1}\right)\left(r_{i,j}+\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}\\ +\frac{h_{i,j+1/2}^3\beta }{12\mu }\left(g_{i,j}-g_{i,j+1}\right)\left(r_{i,j}+\frac{\Delta r}{2}\right)\frac{\Delta \theta }{\Delta r}\end{array}$ (12)

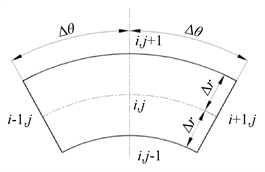
Figure 3. Finite difference mesh generation

图3. 有限差分法网格划分

通过求解式(11)结合边界条件(5)~(8)即可求解雷诺方程。

迭代收敛的判别式为：

$\epsilon =\frac{{\displaystyle \underset{i=1}{\overset{m+1}{\sum }}{\displaystyle \underset{j=1}{\overset{n+1}{\sum }}\left|p_{i,j}^{\left(k+1\right)}-p_{i,j}^{\left(k\right)}\right|}}}{{\displaystyle \underset{i=1}{\overset{m+1}{\sum }}{\displaystyle \underset{j=1}{\overset{n+1}{\sum }}\left|p_{i,j}^{\left(k+1\right)}\right|}}}$ (13)

式中： $\epsilon$ 为迭代精度。

通过上式可以计算液膜压力分布，在计算域内积分可得液膜承载力为：

$F_{K1}=N{\displaystyle {\int }_{R_1}^{R_2}{\displaystyle {\int }_0^{\frac{2\pi }{N}}p\text{d}\theta \text{d}r}}$ (14)

3.4. 精度验证

根据上述数值计算方法编制程序进行计算，并与文献 [10] 结果进行对比验证，如表1所示。可以看出，最高压力和承载力计算结果都与文献中结果吻合，最大偏差不超过5%，证明了程序的正确性。

Table 1. Example verification

表1. 算例验证

3.5. 微凸体接触计算模型

采用G-T模型 [11] 进行微凸体接触计算，数学表达式见下式：

$\{\begin{array}{l}{p}^{\prime }\left(h/\sigma \right)=4.4086\times {10}^{-5}\cdot K\cdot E^{\prime }{\left(4-h/\sigma \right)}^{6.804}\left(h/\sigma <4.0\right)\\ p^{\prime }\left(h/\sigma \right)=0\left(h/\sigma \ge 4.0\right)\end{array}$ (15)

其中：

$\frac{1}{E^{\prime }}=\frac{1}{2}\left(\frac{1-{\gamma }_1^2}{E_1}+\frac{1-{\gamma }_2^2}{E_2}\right)$ (16)

式中： $\sigma$ 是用于表征粗糙表面的量。对于正态分布而言， $\sigma =1.2522Ra$，可以通过 $Ra$ 求取得 $\sigma$ 值 [12]； $E_1$， $E_2$ 分别为涨圈和旋转轴材料的弹性模量； ${\gamma }_1$， ${\gamma }_2$ 为涨圈和旋转轴材料的泊松比；一般取K = 0.002。

由上式即可计算微凸体承载力：

$F_{K1}=N{\displaystyle {\int }_{R_1}^{R_2}{\displaystyle {\int }_0^{\frac{2\pi }{N}}{p}^{\prime }}}\text{d}\theta \text{d}r$ (17)

4. 润滑状态预测

涨圈在稳态下，涨圈轴向力学平衡方程为：

$F_{AB}-F_f=F_{K1}+F_{K2}$ (18)

因此，涨圈主密封端面的润滑状态由液膜压力p与固体接触压力(微凸体) p'决定的，由式(3)和式(15)可见，流体压力p和固体接触力p'只与液膜厚度h有关，液膜厚度通过式(18)迭代计算而来。

定义液膜承载力所占的比例，即液膜承载比为：

$W_f=\frac{F_{K1}}{F_{K1}+F_{K2}}$ (19)

经过求解计算后获得F_K1与F_K2，即可计算出W_f，当 $W_f=\text{1}$ 时为完全流体润滑，当 $0<W_f\le 1$ 时为混合润滑状态。

由迭代后膜厚和相关工况与尺寸参数可以计算主密封面泄漏量如下式 [13]：

$Q_1={\displaystyle {\int }_0^{2\pi }\frac{1}{{\displaystyle {\int }_{R_1}^{R_2}\frac{\text{d}r}{r{h}^3}}}\frac{\Delta p}{12\mu }\text{d}\theta }+{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{R_1}^{R_2}\frac{1}{40\mu }\rho h^2{\omega }^2{r}^2\text{d}r\text{d}\theta }}$ (20)

涨圈主密封面压力计算流程

在软件中进行液膜厚度的迭代，以及涨圈主密封面的液膜压力与微凸体压力的计算，从而判断涨圈的润滑状态。其计算流程如图4所示。

Figure 4. Programming flow chart

图4. 程序设计框图

5. 影响润滑状态因素分析

5.1. 端面几何形貌对润滑状态的影响

端面形貌的变化引起液膜厚度的变化，导致液膜压力发生变化，从而改变主密封面的润滑状态。其中涨圈的结构与工况参数见表2。

Table 2. Structural parameters and working condition parameters of expansion ring

表2. 涨圈的结构参数与工况参数

5.1.1. 锥度对润滑状态的影响

由于机械加工或者工作条件下热变形以及磨损的影响，密封端面可能会产生一定的锥度，此时液膜厚度沿径向是变化的。当端面存在一个锥度时，液膜厚度为：

$h=h_0+b\left(r-R_1\right)$ (21)

式中：b为锥度。

如图5所示，涨圈端面的间隙主要由三种类型，第一种为平行间隙，两密封端面是平行，此时b = 0；第二种为收敛间隙，密封介质从大口进入，小口流出，此时b < 0；第三种是发散间隙，密封介质从小口进入，大口流出，此时b > 0。

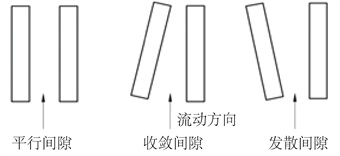
Figure 5. Schematic diagram of end clearance type

图5. 端面间隙类型示意图

图6所示是涨圈端面液膜压力与锥度的关系，可见端面的锥度将会影响流体静压效果，对于发散间隙(b > 0)，液膜压力呈现内凹状，而且锥度越大，液膜承载力就越小；对于收敛间隙(b < 0)，液膜压力呈现外凸状，锥度越大，液膜承载力越大。

将迭代的液膜厚度代入公式(19)中，即可计算得到主密封面泄漏量，锥度与泄漏量的关系如图7所示。由图可见，当两个表面平行时泄漏量最小，无论是收敛间隙还是发散间隙都会增大泄漏量。

5.1.2. 波度对润滑状态的影响

密封面上的波度通常来源于两个方面，一种是由于在加工过程中，从机床到工件系统的周期低频振

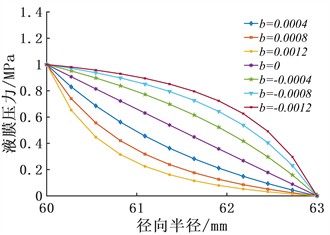
Figure 6. Relationship between liquid film pressure and taper

图6. 液膜压力与锥度关系

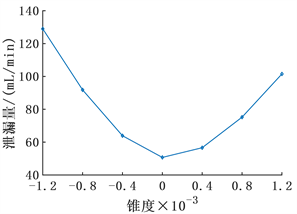
Figure 7. Variation of leakage with taper

图7. 泄漏量随锥度的变化情况

动；另一种是为了改善润滑条件人为引入波度。波度的产生导致液膜厚度沿周向发生变化，在波度相对较大时会使端面发生空化现象，本文针对波度问题进行相关分析。对于具有周期性波度的端面密封，其液膜厚度满足下式：

$h=h_o+h_w\cos \left(n_w\theta \right)$ (22)

式中：h_w为波幅，单位为µm；n_w为波数。

对波幅 $h_w=\text{2}\mu \text{m}$，波数 $n_w=3$，粗糙度 $\sigma =0.5$ 的密封表面进行研究，由于膜厚分布具有周期性可以取一个波进行研究，其液膜压力如图8所示，液膜压力分布图上有一个压力峰和一个空化区，这是因为膜厚沿周向先减小后增大，波峰出现的位置对应了液膜收敛区，而空化现象出现在液膜发散区，这说明波度的出现产生了明显的流体动压效应。

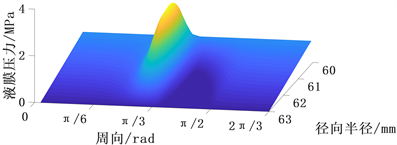
Figure 8. Liquid film pressure diagram considering waviness

图8. 考虑波度的液膜压力图

微凸体压力分布如图9所示，在液膜较小的地方微凸体接触压力较大，而在液膜较厚的地方即当液膜h与σ的比值大于4时两个表面被液膜完全隔开此时微凸体压力为0。

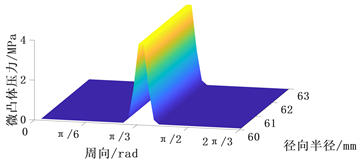
Figure 9. Pressure distribution diagram of micro convex body considering waviness

图9. 考虑波度的微凸体压力分布图

波度端面的几何参数有波幅、波数和表面粗糙度，下面分别研究表面粗糙度以及波幅h_w与波数n_w对润滑状态的影响。

5.1.3. 波幅对润滑状态的影响

如图10所示，随着波幅的增加，液膜承载比也逐渐增强，但是增长效果并不明显，波幅为5 µm时，承载力占比为66%，仅比流体静压高12%。图11显示随着波幅增大，泄漏量大幅增加。

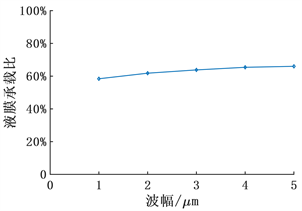
Figure 10. Variation of liquid film bearing ratio with wave amplitude

图10. 液膜承载比随波幅的变化规律

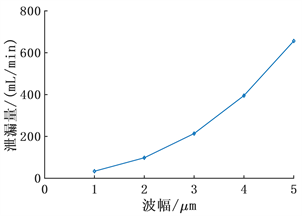
Figure 11. Variation law of leakage with wave amplitude

图11. 泄漏量随波幅的变化规律

5.1.4. 波数对润滑状态的影响

保证波幅不变 $h_w=\text{3}\mu \text{m}$，研究波数对润滑状态的影响。其结果如图12与图13所示。由图13可见泄漏量的增大的并不明显。而从图12可见波数对液膜承载力的影响相对更加显著，波数从2个增加到6个，泄漏量仅仅增加了7 mL/min，但是却让液膜承载占比增大了15%。

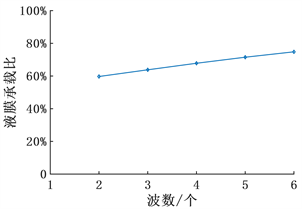
Figure 12. Variation of liquid film bearing ratio with wave number

图12. 液膜承载比随波数的变化规律

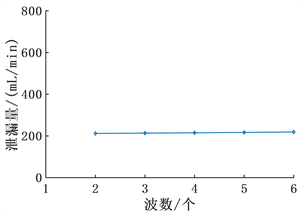
Figure 13. Variation law of leakage ratio with wave number

图13. 泄漏量随波数的变化规律

5.1.5. 表面粗糙度对润滑状态的影响

分别取三种不同的端面形貌：h_a (波幅1 µm，波数6个)，h_b (波幅2 µm，波数10个)，h_c (波幅3 µm，波数12个)，研究表面粗糙度对润滑状态的影响。如图14、图15所示是表面粗糙度对液膜承载能力与泄漏量的影响，可以看出表面粗糙度对液膜承载力影响很大，当表面粗糙度为0.2时三种不同的端面形貌所产生的液膜动压力达到100%，随着表面粗糙度增大，流体动压效果逐渐降低，可见表面粗糙度是决定流体动压效果的关键因素，当粗糙度过大时，即使增大波数与波幅也很难改善密封的润滑效果。由图15可见，泄漏量也随着粗糙度的增大而增大，因此降低表面粗糙度是提升密封性能的必要条件。

5.2. 操作参数对润滑状态的影响

液膜承载力与操作参数息息相关，其中密封介质压力是液膜承载力的来源，没有介质压力，意味着端面承载力完全由微凸体承载力提供，这样导致摩擦磨损严重，在没有润滑油的情况下，密封环很快就会失效；而旋转轴的转速与密封介质粘度对流体动压效应以及端面的泄漏量有很大的影响，因此研究介质压力、旋转轴的转速与密封介质粘度与密封性能的关系十分重要。

Figure 14. Variation of liquid film bearing ratio with surface roughness

图14. 液膜承载比随表面粗糙度的变化规律

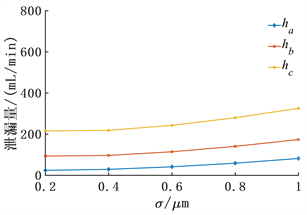
Figure 15. Variation law of leakage with surface roughness

图15. 泄漏量随表面粗糙度的变化规律

5.2.1. 压差对润滑状态的影响

由图16可见，随着密封介质压差的增大，液膜承载比逐渐降低，这是因为密封介质压差的增大导致闭合力增大，需要通过减小膜厚来提高液膜承载力和微凸体承载力，从而让闭合力和开启力平衡，因此微凸体承载力与液膜承载力不断增大，而微凸体承载力增大幅度高于液膜承载力，使得液膜承载比逐渐减小，可见在高介质压力下，密封情况会变恶劣。图17是泄漏量与压差的关系，可以看出随着压差增大，泄漏量也是逐渐增大的。

Figure 16. Variation law of leakage ratio with pressure difference

图16. 液膜承载比随压差的变化规律

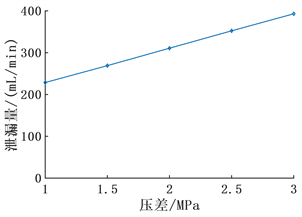
Figure 17. Variation law of leakage with differential pressure

图17. 泄漏量随压差的变化规律

5.2.2. 密封介质粘度对润滑状态的影响

由图18可见，介质粘度的提高可以大幅度的提高液膜承载比，所以高粘度的密封介质更容易隔开摩擦面从而形成完全流体润滑。所以可以确定在低粘度情况下，占主导作用的是流体静压，流体动压效应较弱，而在高粘度的情况下，不仅有流体静压而且具有很强的流体动压。图19是泄漏量随动力粘度变化规律，由图可以看出，在介质粘度较低的情况下，泄漏量的很大，随着粘度增大，泄漏量逐渐减低并趋于平稳。

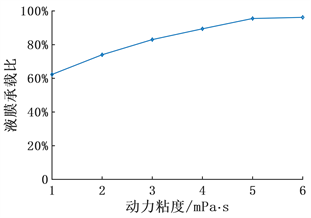
Figure 18. Variation law of leakage ratio with viscosity

图18. 液膜承载比随粘度的变化规律

Figure 19. Variation law of leakage with viscosity

图19. 泄漏量随粘度的变化规律

5.2.3. 旋转轴转速对润滑状态的影响

由图20可以看出，随着转速升高，液膜承载能力逐渐增大，这表明转速可以提升流体动压效应，在转速越高的情况下越容易形成完全流体润滑，图21表明转速的升高导致泄漏量大幅度的增加，这是因为转速升高导致离心作用增强，从而导致泄漏量大大增加。

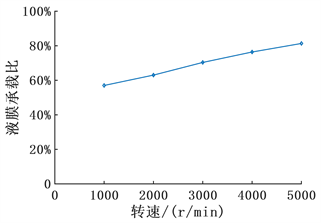
Figure 20. Variation of liquid film bearing ratio with rotating speed

图20. 液膜承载比随转速的变化规律

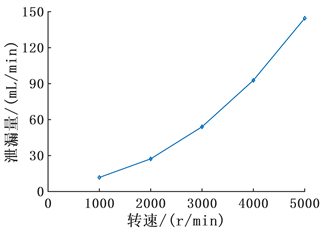
Figure 21. Variation law of leakage with rotating speed

图21. 液膜承载比随转速的变化规律

6. 结论

本文首先对涨圈的润滑状态进行了研究，进而针对涨圈密封的润滑状态建立稳态情况下主密封压力场的平衡方程，通过建立模型来计算端面的液膜压力与微凸体压力的分布，随后研究端面几何形貌和操作参数对密封性能的影响，主要结论如下：

1) 针对涨圈润滑状态的特点，并依据涨圈在轴向的受力情况，提出了在稳态情况下的平衡方程即：密封介质产生的闭合力与液膜和微凸体产生的开启力平衡。基于流体润滑基本方程即雷诺方程，建立液膜压力分布模型，通过数值解法–有限差分法对液膜压力求解，进而计算出液膜所产生的承载力，最后将计算结果与文献结果对比，验证程序设计的可靠性；建立微凸体接触模型，计算微凸体压力分布，并依据稳态情况下的平衡方程，对液膜厚度进行迭代计算，保证闭合力与开启力平衡。

2) 在给定涨圈结构参数与密封参数的情况下，研究不同端面形貌对润滑状态和泄漏量的影响。对于锥度的研究结果表明：无论是正锥度还是负锥度都会增大密封的泄漏量，其中正锥度对密封性能的影响更加恶劣，涨圈密封应该在避免出现正锥度的同时，尽量减小端面负锥度，以满足泄漏量要求；对于波度的研究结果表明：增大波幅在提升液膜压力的同时会大幅增加泄漏量，而增大波数在小幅增加泄漏量的同时能够较大幅度提高液膜承载力，因此在设计波度型的端面密封时可以保证泄漏量的情况下合理提高波幅和波数；表面粗糙度是影响流体动压效应的重要因素，表面粗糙度过大时，无论如何增大端面的几何结构尺寸，都难以产生较大的流体动压力，所以为了改善端面的润滑作用首先需要考虑降低密封端面的表面粗糙度。

3) 对操作参数的研究表明：介质压差增大会使闭合力增加从而减小液膜厚度，同时增加泄漏量、液膜承载力以及微凸体承载力，但是总体上来讲液膜的承载比会降低，即密封介质压力越高，润滑条件越恶劣；密封介质的粘度与旋转轴转速越高，液膜的产生动压效应越强，液膜承载力也会越大，润滑状态逐步向完全流体润滑转变，降低泄漏量。