一种高精度太阳能跟踪控制系统设计与实现

Design and Implementation of a High-Precision Solar Tracking Control System

摘要: 为了提高线性菲涅尔式聚光镜场的跟踪控制精度，本文基于PLC研制了原理样机模型，对太阳进行实时跟踪。基于光控和程控相结合，对天气的阴晴判断提出了一种基于模糊识别原理的全天候太阳自动跟踪方法，在Matlab中建立了阴晴模糊识别系统，然后通过高精度太阳位置算法，实现对聚光镜场的高精度和低延迟的跟踪控制目标。结果表明：通过误差分析法计算并比较跟踪目标角度计算结果与德国弗朗霍夫研究所提供的目标角度计算结果的理论值得出跟踪绝对误差在±0.455˚以内，具有较高的实用性和广阔的发展前景。

Abstract: In order to improve the tracking control accuracy of linear Fresnel-type concentrating mirror field, this paper develops a principle prototype model based on PLC to track the sun in real-time. Based on the combination of optical control and program control, an all-weather automatic sun tracking method based on the fuzzy recognition principle is proposed for the cloudy and sunny judgment of weather, and a fuzzy recognition system for cloudy and sunny is established in Matlab, and then the high-precision sun position algorithm is used to achieve a high-precision and low-delay tracking control target for the spotting mirror field. The results show that: The theoretical value of the tracking target angle calculation results calculated by the error analysis method and compared with the target angle calculation results provided by the Fraunhofer Institute in Germany is within ±0.455˚ of the absolute tracking error, which has high practicality and broad development prospects.

1. 引言

碳达峰、碳中和 [1] [2] 对能源转型提出了更为迫切的诉求，能源行业碳排放占全国碳排放总量的80%左右，实现“双碳”目标需要能源行业贡献更大的减碳比例。对我国能源行业而言，实现碳中和的目标给其转型带来了利好机遇，但同时也使其面临短期内任务重、负碳技术未成熟、新能源缺乏竞争优势等挑战。

近些年，为了实现可持续发展，世界各国集中精力从传统化石能源转向各种清洁能源，清洁能源技术包括太阳能 [3] [4]、水能 [5]、风能 [6]、生物质能 [7] 和地热资源能 [8] 等，其中太阳能不用运输且清洁安全，是目前世界上可再生能源领域内不可缺少的重要部分，对可再生能源领域有着至关重要的作用。如何有效的提高太阳能的利用率，将极大解决世界上能源稀缺的难题。太阳能资源“取之不尽，用之不竭”，是当前可再生能源开发利用领域内的不可缺少的组成部分，近几年太阳能光热发电来受到人们的高度关注 [9] [10]。2016年9月13日国家能源局公布国内20家企业成功入围首批太阳能热发电示范项目(2018年底建成项目执行每度1.15元上网标杆电价 [11])，标志着我国太阳能光热发电产业正式启动。

针对太阳跟踪技术的应用，国内外学者进行了大量的研究，Abdallah等学者对光伏发电采用双轴太阳自动跟踪，发电效率比固定式光伏发电效率提高41% [12]；Al-Soud等学者研制了针对太阳灶的自动跟踪控制系统，太阳灶跟踪太阳使集热器达到600℃以上 [13]；纪浩 [14] 学者通过系统自动接收GPS信号来计算太阳位置，从而实现对线性菲涅尔系统的集热效率的提升。线式聚光系统主要有槽式和菲涅尔，整体结构相对简单、耗材少，但系统结构相对庞大，抗风性差。而塔式和碟式则为点式聚光系统，均采用双轴跟踪方式。

基于此，本文提出了一种高精度太阳跟踪装置，基于光控和程控相结合，对天气的阴晴判断提出了一种基于模糊识别原理的全天候太阳自动跟踪方法，在Matlab中建立了阴晴模糊识别系统，然后通过高精度太阳位置算法，从而得到太阳实时位置情况，将跟踪误差控制在可接受的范围内，对太阳能光热发电厂具有很高的实用性和广阔的发展前景。

2. 太阳能跟踪系统工作原理

2.1. 太阳能跟踪系统结构框图

太阳能跟踪控制系统主要包括PLC控制系统、电源转换模块、信号传输模块、通讯模块、操作模块、上位机等组成，如图1所示为镜场控制系统结构。

在PLC控制系统中，应用了一种高精度的太阳位置算法，通过已知当地实时的日期和时间、地理经度和纬度，对太阳的高度角和方位角度进行高精度的计算。通过对太阳位置的准确计算，得到的数据由编码器或限位开关通过PLC将传送给跟踪控制系统，跟踪控制系统下达命令使聚光镜场按照所得的太阳位置进行旋转，控制器得到输出指令驱动电机进行追踪太阳，从而让聚光集热器旋转到高精度计算出太阳位置相对的方向。

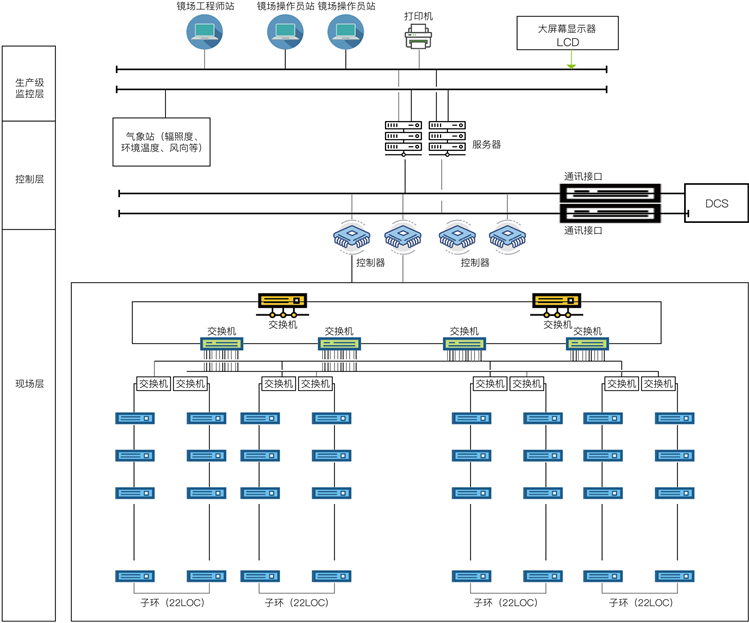
Figure 1. Structure block diagram of solar tracking control system

图1. 太阳能跟踪控制系统结构框图

2.2. 基于阴晴判断的全天候太阳自动跟踪

本文通过将目前发电领域比较常用的两种跟踪方式视日运动轨迹算法和光电跟踪法相结合，从而弥补单独采用单独跟踪时的缺陷，所以系统对天气的状况要进行准确的判断。基于此，本文提出一种基于天气阴睛判断自动式全天跟踪方式，对不同的天气状况进行准确判断，对不同的天气状况采用最适合的跟踪方式。

1) 模糊识别的原理 [15]

假设对于一个有n个特征值的参考对象，设这n个特征值的隶属度分别为 ${\mu }_1,{\mu }_2,\cdots ,{\mu }_n$，隶属度的权值为： ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$，M为设定一个阈值，

若满足：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i{\mu }_i\ge M}$ (1)

则认为此事物满足要求，并由此进行分类。

2) 模糊识别方法

根据最大隶属原则，对识别对象进行分类。设论域U中n个模糊子集分别为 $A_1,A_2,\cdots ,A_n$， ${\mu }_1\left(x\right),{\mu }_2\left(x\right),\cdots ,{\mu }_n\left(x\right)$ 分别是对应的隶属度函数，若被识别对象 $x_0=U$，则：

$A_i\left(x_0\right)=\max \left\{{\mu }_1\left(x_0\right),{\mu }_2\left(x_0\right),\cdots ,{\mu }_n\left(x_0\right)\right\}$ (2)

则第i类模糊子集为x₀。

本文分别从建立输入、输出变量隶属度函数以及模糊规则三个步骤对模糊识别系统 [6] [7] 进行建立。

3) 输入变量隶属度函数

将光强大小和光强变化选为输入变量隶属度函数的特征。光强大小分为强光、中等光和弱光之分，光强变化则设为大和小。隶属度函数类型选用高斯曲线，设光强取值范围为[0~10]，光强变化值的取值范围为[0~10]。

如表1和表2所示为输入变量值。

Table 1. Output variable value of light intensity magnitude

表1. 光强大小的输出变量值

Table 2. Output variable values for light intensity changes

表2. 光强变化的输出变量值

4) 输出变量隶属度函数

输出变量隶属度函数将晴天、多云和阴天三种天气作为输出变量，隶属度函数类型选用三角形，输出变量值见表3所示。

5) 模糊推理规则

综上所属，可得模糊规则如下表4所示：

Table 3. Output variable value

表3. 输出变量值

Table 4. Fuzzy reasoning rules

表4. 模糊推理规则

在系统中输入上述所对应的模糊判断规则。

2.3. 模糊推理及仿真结果

试验发现，光强值范围在[30~300] mA，光强变化值范围为[0~180] mA，现对实际光强值及光强变化值做一些线性处理：

设实际光强值为P，光强最大值和最小值分别设为P_max和P_min，对其进行线性处理后为：

$P_1=10\cdot \frac{\left(P-P_{\min }\right)}{P_{\max }-P_{\min }}$ (3)

同理对光强变化值也做该线性处理。

将上述线性处理过的光强值和光强变化值输入到系统中，则得到仿真结果如图2所示。

根据规则观察器可得，选取不同输入的光强值和光强变化值时，来验证推理的天气类型能否符合实际的需求。结果如表5所示：

如图2(b)所示为天气类型的映射曲线图，通过仿真结果利用模糊识别理论对天气类型的识别具有准确性和可行性。

3. 太阳能跟踪控制系统的设计

3.1. 视日运动轨迹模型

对于太阳主动式跟踪来说，精准计算太阳的位置可提高太阳的跟踪精度，对于目前公认的高精度太阳位置的计算SPA算法 [16] [17] 来说，在工程应用上需要极其复杂的计算过程，给编程上带来了极大的难度。所以本文应用简单易行的太阳位置跟踪算法并通过验证在精度上能够满足工程应用上的实际需求。

首先对太阳运行轨迹跟踪模型进行建立，如图3所示。当确定了太阳跟踪控制系统所在地的经纬度和观测时间，通过高精度的太阳位置算法，就能推导出此刻太阳的赤纬角和时角值，根据所得到的上述值，推到出所在地此时的太阳方位角a_s和高度角 ${\gamma }_s$。

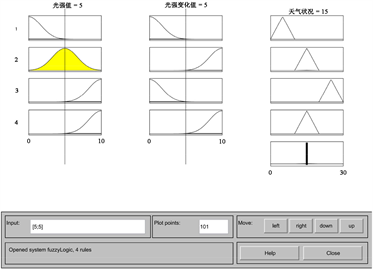(a) 规则观察器 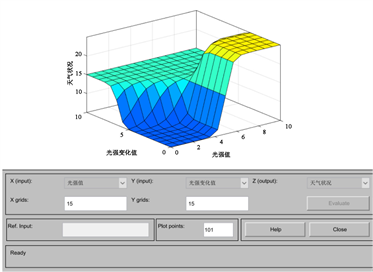(b) 天气类型的映射的曲线图

Figure 2. Simulation results

图2. 仿真结果

Table 5. Simulation results

表5. 仿真结果

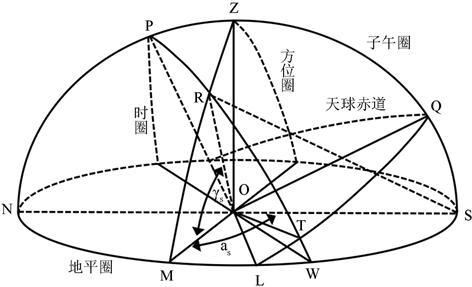
Figure 3. Solar orbit tracking model

图3. 太阳运行轨迹跟踪模型

1) 太阳赤纬角 $\delta$

1985年，Bourges [18] 给出了太阳赤纬角 $\delta$ 的计算公式：

$\begin{array}{l}\delta =0.3723+23.2567\cdot \sin \left({\omega }_{0}t\right)+0.1149\sin \left(2{\omega }_{0}t\right)-0.1727\sin \left(3{\omega }_{0}t\right)\\ -0.7580\cos \left({\omega }_{0}t\right)+0.3656\cos \left(2{\omega }_{0}t\right)+0.0201\cos \left(3{\omega }_{0}t\right)\end{array}$ (4)

${\omega }_0=\frac{2\text{π}}{365.2422}$

其中： $t=n-1-n_0$

$n_0=78.801+\left[0.2422\left(\text{year}-1969\right)\right]-\mathrm{int}\left(0.25\left(\text{year}-1969\right)\right)$

式中，n为日子序数。

1991年，王炳忠和刘庚山 [19] 对Brouges算法进行了优化，使其精度大大提高，其公式为：

$n_0=79.6764+\left[0.2422\left(\text{year}-1985\right)\right]-\mathrm{int}\left(0.25\left(\text{year}-1985\right)\right)$

2) 太阳时角 $\omega$

其公式为：

$\omega =\frac{{\tau }_{\theta }-720}{4}$ (5)

式中， ${\tau }_{\theta }$ 为观测地的时间。真太阳时和北京时间的关系可有式(2.4)求得：

${\tau }_{\theta }=北京时间+4\cdot \left(120-L_{loc}\right)+eot$ (6)

式中，L_loc为当地经度；eot是由地球公转产生偏差。1981年，lamm [20] 给出了时差计算方法，其公式为：

$eot={\displaystyle \underset{k=0}{\overset{5}{\sum }}\left[A_k\cdot \cos \left(\frac{2k\text{π}N}{365.25}\right)+B_k\sin \left(\frac{2k\text{π}N}{365.25}\right)\right]}$ (7)

式中，N为闰年第一天开始的某一天顺序数；A_k和B_k的取值见表6所示。

Table 6. Values of parameters Ak and Bk

表6. 参数A_k和B_k的值

3) 阳角的计算

太阳高度角 ${\gamma }_s$ 的计算公式如下：

$\sin {\gamma }_s=\cos {\theta }_z=\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega$ (8)

其中某一时刻所在地的纬度为 $\Phi$。

当太阳垂直照射时，即在中午时刻， $\omega$ = 0， $\cos \omega$ = 1，上述公式则为：

$\sin {\gamma }_s=\cos \left(\varphi -\delta \right)=\sin \left[{90}^{\circ }\pm \left(\varphi -\delta \right)\right]$ (9)

当太阳的位置正好处在天顶位置北面，太阳实际垂直照射时，即 $\Phi <\delta$，上述公式化简为：

$\sin {\gamma }_s=\cos \left(\varphi -\delta \right)=\sin \left[{90}^{\circ }+\left(\varphi -\delta \right)\right]$ (10)

${{\displaystyle \gamma }}_s={90}^{\circ }+\left(\varphi -\delta \right)$ (11)

当太阳的位置正好处在天顶位置南面时，太阳实际垂直照射时，即 $\Phi >\delta$，上述公式化简为：

$\sin {\gamma }_s=\sin \left[{90}^{\circ }-\left(\varphi -\delta \right)\right]$ (12)

${{\displaystyle \gamma }}_s={90}^{\circ }-\varphi +\delta$ (13)

太阳方位角a_s的计算公式如下：

$\sin a_s\frac{\cos \delta \sin \omega }{\cos {\gamma }_s}$ (14)

3.2. PLC控制程序流程

如图4所示为系统流程图，首先系统将进行初始化，其次设置系统的相关参数，待一切准备工作完成后，需要先判断控制是否在自动位置，这时需要人工对其进行手动调节；完成上述指令后，系统首先

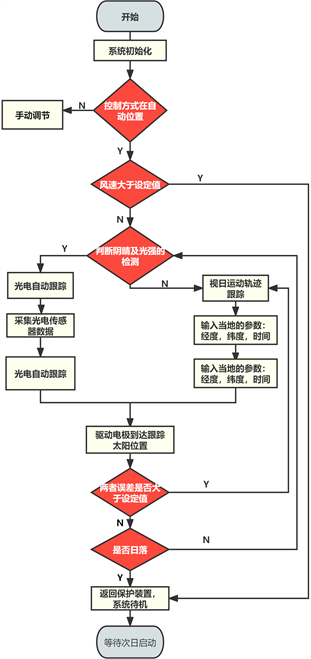
Figure 4. PLC control program flow chart

图4. PLC控制程序流程图

进入风速检测状态，判断是否能进行正常的工作运行，若风速大于设定的值，系统则将进入避风保护状态，使聚光器回归初始状态；然后系统进入阴晴模糊识别系统，结合光强值，光强变化值以及光电传感器的短路电流值，对天气阴晴模糊识别进行准确的判断，通过天气的阴晴来判断使用光电式跟踪法或太阳视日运动轨迹跟踪法，驱动电机追踪太阳，从而实现更精准的跟踪；程序采取每一分钟为间隔自动记录目标角度，每隔30分钟校准一次聚光结果，待到太阳落山时，集热装置接到系统指令，返回初始状态，待次日重新启动，控制器的时钟芯片每天早晨5:00唤醒控制器，系统开始工作。

4. 实验测试结果

本文测试地点选在兰州市安宁区(103.726389˚E, 36.1055556˚N)，聚光镜场采用东西水平布置。通过选定2021年中4个典型具体日期依次是：春分日(2021年3月20日)、夏至日(2021年6月21日)、秋分日(2021年9月23日)以及冬至日(2021年12月21日)对跟踪目标角度进行应用试验，从而对跟踪控制系统的性能进行分析。对4个典型日期的太阳进行全天式的跟踪，记录控制系统中太阳高度角、方位角以及跟踪目标角的数据变化，从而分析线性菲涅尔式聚光镜场的跟踪控制系统的运行特性。

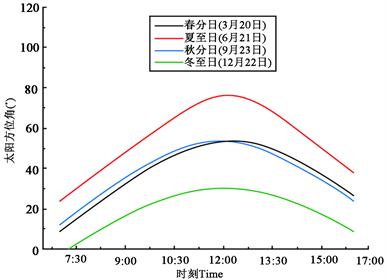
如图5所示为系统所记录全天试验测量4个典型日期的太阳高度角和方位角的变化曲线图。太阳高度角变化呈先增长后降低的趋势，在正午时分达到高度角的峰值，其中夏至日的高度角峰值为77.25˚，其整日高度角的变化范围也为最大。而冬至日的高度角峰值最低，且为30.45˚，夏至日与冬至日高度角峰值尽相差46.80˚，如图5(a)所示。4个典型日期的方位角转动轨迹类似，夏至日的方位角变化范围为全年的最大值，5:00的方位角为61.54˚，19:00的方位角为296.55˚，变化了235.01˚。冬至日的方位角的变化范围也为四个里面的最小值，变化了156.86˚，如图5(b)所示。一年中太阳的运动规律存在着较大的差异，其运行轨迹发生变化非常复杂。

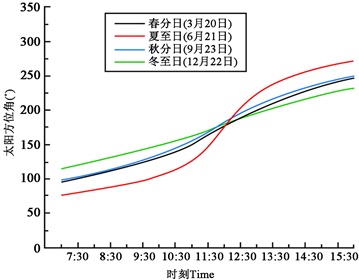(a) (b)

Figure 5. Change curves of solar altitude angle and azimuth. (a) Solar altitude angle; (b) Solar azimuth

图5. 太阳高度角和方位角变化曲线。(a) 太阳高度角；(b) 太阳方位角

典型日跟踪目标角计算结果与德国弗朗霍夫研究所提供的目标角计算结果的理论值误差如图6所示，可以发现，跟踪目标角度计算结果的理论值得出跟踪绝对误差在±0.455˚以内，系统稳定，运行符合预期。

5. 总结

通过对选取的4个典型日期的高度角、方位角和目标跟踪角度进行记录分析，研究聚光器的运行基本特性。分析表明：太阳高度角变化呈先增长后降低的趋势，正午时分达到高度角的峰值；夏至日的

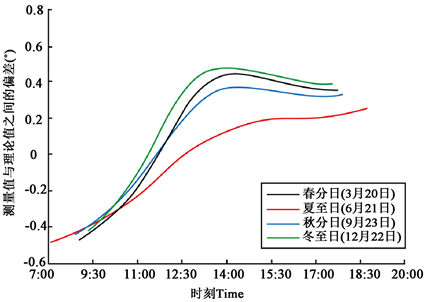
Figure 6. Typical daily tracking angle error curve

图6. 典型日跟踪角度误差曲线

方位角变化范围最大，冬至日方位角变化范围最小；目标跟踪角度在夏至日运行的轨迹范围最大，冬至日运行轨迹范围最小；通过误差分析法计算并比较跟踪目标角度计算结果与德国弗朗霍夫研究所提供的目标角度计算结果的理论值得出跟踪绝对误差在±0.455˚以内，系统稳定，运行符合预期。该跟踪控制系统具有实时性和同步性能，可以很好满足线性菲涅尔式聚光镜场要求。

NOTES

^*通讯作者Email: [e-mail]