基于遗传模拟退火算法的重频选择

Pulse Repetition Frequency Sets Selection Based on Genetic Simulated Annealing Algorithm

摘要: 中重频脉冲多普勒雷达能够在距离和速度两个维度上较好地实现目标和杂波的区分，具有良好的强杂波抑制能力，广泛地应用于各类雷达系统。其中，重频选择是中重频雷达设计中重要的一环。基于N/M检测准则，合理的重频组合能够有效地缩减距离速度二维遮蔽区域面积，提升雷达探测性能。本文针对重频组合选择问题，提出了一种基于遗传模拟退火算法的中重频优化选择算法。该算法结合了遗传算法和模拟退火算法，克服了“早熟”现象，提升了优化效率。试验表明，相较于单纯的遗传算法和模拟退火算法，该算法能够更有效、更快速地获得最优重频组合。

Abstract: Medium pulse repetition frequency pulsed-Doppler radars can distinguish clutter and targets in both range space and Doppler space clearly. It brings favorable clutter suppression ability and widely application in various radar systems. The selection of multiple pulse repetition frequency sets plays an important role. Based on N/M detection rule, felicitous sets can compress the blind zones of range and Doppler and improve the radar system performance. The paper proposed a method for medium pulse repetition frequency set selection, based on genetic simulated annealing algorithm. The method inosculates the evolution algorithm and the simulated annealing algorithm. It avoids the early convergence and improves the optimization performance. The results show that the method acquires optimum medium pulse repetition frequency set more effectively, compared with genetic algorithm or simulated annealing algorithm.

1. 引言

重频选择在现代雷达系统设计中具有重要意义。低重频设计具有距离维不模糊的特点，可直接获得目标的真实距离，但同时由于重频低，杂波带宽占比大，滤波后会造成多普勒可见性的缺失，造成多普勒维上的目标遮蔽，进而影响探测性能。高重频雷达具有在多普勒(速度)维上不模糊的特点，可以直接获得目标的真实速度，但由于多次的距离折叠，目标与近区强杂波(地面雷达)或副瓣杂波(机载雷达)折叠在一起，降低目标的信杂噪比，进而影响探测性能。中重频雷达是对两者的折中，其可在距离维和多普勒维上对目标和杂波进行有效的区分，实现目标的检测。

单一重频会在距离维和速度维上产生遮蔽，造成遮蔽区域目标的丢失；不同重频的遮蔽区域不同，彼此之间具有互补性。中重频脉冲多普勒雷达通过发射M个不同重频的脉组，并采用N/M检测准则来降低遮蔽区域面积。由于重频的可选择范围很广，使得最优/近似最优重频的选择成为了一个复杂的组合优化问题，难以通过遍历实现最优重频组合的求解。常见的重频组合优化算法有遗传算法、模拟退火算法等 [1] [2] [3] [4]。

Davies, P.G.等人提出了利用遗传模拟算法的雷达重频选择方法。遗传算法是模拟生物遗传进化过程而形成的一种自适应全局优化概率搜索方案，具有强大的全局搜索能力，能够有效解决离散变量的优化组合问题。该方法利用了遗传算法强大的全局搜索能力，可有效解决离散变量优化组合问题的特性，实现了重频组合的优化迭代。但由于个体适应度的逐渐趋于一致，使得其易出现早熟现象，局部搜索能力较差。葛建军、张春城等人提出了利用模拟退火算法进行雷达重频选择的方法。模拟退火算法是模拟固体退火原理，通过产生新解，并按照一定的概率接受新解，通过多次迭代来逐步获得最优解/近似最优解。该算法能够避免陷入局部最优解，基于适当的初始值，该算法能够更为快速的获得更优的重频组合。但受限于初始值的设定，模拟退火算法容易陷入局部最优解，导致搜索时间过长。

为快速获得雷达重频组合的最优解，本文提出了一种基于遗传模拟退火算法的重频优化选择方法。该算法采用与遗传算法相似的方式随机产生初始群体，并进行交叉、变异产生新个体。但在选择过程中，采用Metropolis接受准则进行子代个体的选择。在算法初期，个体差异较大，拉伸作用对算法收敛影响不大，能够实现快速收敛，在优化后期，拉伸作用可使得个体之间存在一定的差异性，克服了算法早熟，能够更快地收敛到全局最优解。该算法有效结合了遗传算法和模拟退火算法两者的优势，既具备强大的全局搜索能力，实现快速收敛，也能够实现高效的局部最优解性能，获得全局最优解。

2. 重频选择

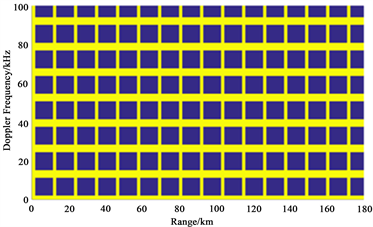
对于脉冲多普勒雷达来说，每个重频对应着特定的速度和距离盲区，如图1所示。其中，黄色区域为不可见区域，蓝色区域时可见区域。当目标位于黄色区域对应的距离或多普勒频移时，雷达是无法发现该目标的。当雷达发射多个不同重频的脉组，并采用N/M检测准则进行目标检测时，可以实现大幅降低黄色区域的面积。图2所示为随机选择8组重频，并采用3/8检测准则获得的遮蔽图。对比图1和图2可知，采用多重频组合和N/M检测准则，能够有效的减少距离和速度遮蔽对探测的影响。

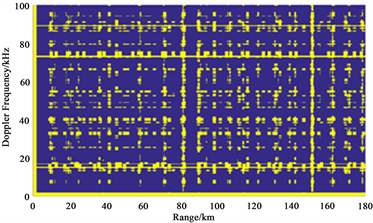(a) (b)

Figure 1. Schematic diagram of range/Doppler shadowing rate. (a) Schematic diagram of the shadowing rate under a single repetition frequency; (b) schematic diagram of the shadowing rate under 3/8 detection criterion

图1. 距离/多普勒遮蔽率示意图。(a) 单重频下遮蔽率示意图；(b) 3/8检测准则下遮蔽率示意图

3. 算法简介

遗传模拟退火算法是将遗传算法与模拟退火算法结合所形成的一种算法。该算法具有更优良的性能，相较于结合前的单一算法，在全局搜索能力和收敛性上具有较大的优势 [4] [5] [6] [7]。其操作流程如图2所示。下面结合重频选择问题进行详细描述。

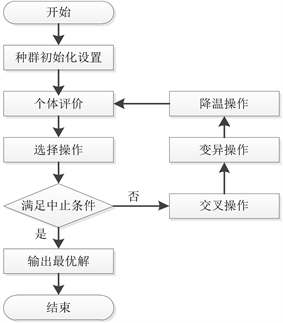
Figure 2. The flow chart of the genetic simulated annealing algorithm

图2. 遗传模拟退火算法流程图

根据雷达系统设计，可知雷达的探测范围 $\left[R_{\min },R_{\max }\right]$ ( $R_{\max }$ 为最大探测距离， $R_{\min }$ 为近程盲区)，距离分辨单元 $\Delta R$ ；雷达工作频率 $f$，最大目标探测速度 $V_{\max }$，多普勒量化步长 $B_{pd}$。

据此可得，距离单元数为：

$N_R=\frac{R_{\max }-R_{\min }}{\Delta R}$ (1)

多普勒单元数为：

$N_{freq}=\frac{2\cdot V_{\max }\cdot f_0}{c\cdot B_{pd}}$ (2)

其中，c为光速。

1) 种群初始化主要完成种群初始化设置，确定种群规模 $N_c$，并随机产生 $N_c$ 个个体组成初始化群体。

根据雷达系统探测距离范围和占空比等因素，确定雷达脉冲重复频率的选择范围 $\left[Pr{f}_{\min },Pr{f}_{\max }\right]$，其中 $Pr{f}_{\max }=2R_{\min }/c$， $Pr{f}_{\min }=2R_{\max }/c$。从中随机选取M个重复频率 $\left(Pr{f}_{1,1},Pr{f}_{1,2},\cdots ,Pr{f}_{1,M}\right)$，对每个重频进行二值编码，并将得到的二值编码串联，得到一个重频组合 $S_1$，重复该过程 $N_c$ 次，得到重频组合的群体 $SS=\left[S_1,S_2,\cdots ,S_{Nc}\right]$。

2) 个体评价实现群体内个体的适应度值计算，对群体内的各重频组合的遮蔽区域进行计算。

根据雷达系统参数设计，可知不模糊距离单元数为：

$N_{R\_na}=\frac{c}{2\cdot Pr{f}_{i,j}\cdot \Delta R}$ (3)

其中， $Pr{f}_{i,j}$ 为第 $i$ 个重频组合中的第 $j$ 个重复频率， $i\in \left(1,2,\cdots ,N_c\right)$， $j\in \left(1,2,\cdots ,M\right)$。不模糊多普勒单元数为：

$N_{freq\_na}=\frac{Pr{f}_{i,j}}{B_{pd}}$ (4)

根据脉冲宽度 $\tau$ 和杂波宽度，可知距离和多普勒遮蔽单元分别为：

$\begin{array}{l}{N}_{R\_zb}=\left[0,\frac{c\cdot \tau }{2\Delta R}\right]+N_{Rr}\frac{c}{2\cdot Pr{f}_{i,j}\cdot \Delta R}\\ N_{freq\_zb}=\left[-\frac{W_C}{B_{pd}},\frac{W_C}{B_{pd}}\right]+N_{fr}\cdot \frac{Pr{f}_{i,j}}{B_{pd}}\end{array}$ (5)

其中， $W_C$ 为杂波宽度， $N_{Rr}$ 为距离模糊次数， $N_{fr}$ 为多普勒模糊次数。根据公式(5)，可以求得各重复频率在最大探测距离和多普勒范围内的遮蔽率情况。遮蔽率为不可见单元数量与总的单元数量的比值。

重复上述过程M次，可得重频组合 $S_i$ 内各重频的遮蔽情况。利用利用N/M检测准则对重频组合 $S_i$ 的遮蔽情况进行检测，统计计算遮蔽面积，遮蔽面积的倒数即为重频组合 $S_i$ 的适应度值 $G_i$。通过重复可以获得群体内所有重频组合的适应度值。

3) 选择操作采用Metropolis接受准则对待选择的个体进行选择。

Metropolis接受准则表达式如下：

$P\left(\Delta E,T\right)=\{\begin{array}{c}1\Delta E\le 0\\ {\text{e}}^{-\Delta E/T}\Delta E>0\end{array}$ (6)

其中，P为接受新的重频组合的概率，为新的重频组合与原重频组合适应度值的差值；T为温度控制参数，该值随着迭代次数的增加而不断减小。

将新重频组合与原重频组合对应的遮蔽率进行计算比较，按照Metropolis接受准则，选择是否接受新的重频组合。

4) 满足中止条件：中止条件可以根据重频组合的遮蔽率或者循环次数进行设定，即当群体中某一重频组合的适应度值满足条件时，跳出循环并输出最优解。

5) 交叉及变异操作

从重频组合的群体中随机抽取两个重频组合 $S_{x1}$ 和 $S_{y1}$，根据重频组合的编码长度，选择其中1个或多个交叉点，对两个重频组合进行交叉，得到交叉后的重频组合 ${S^{\prime }}_{x1}$ 和 ${S^{\prime }}_{y1}$。按照变异概率 $P_{ch}$，对重组后的重频组合进行二进制变异，得到变异后的重频组合 ${S^{″}}_{x1}$ 和 ${S^{″}}_{y1}$。

在重频组合群体中的剩余重频组合中，继续抽取两个重频组合，重复上述过程，直到群体所有的重频组合均已完成上述过程。最终得到扩充后的群体。

6) 降温操作

遗传模拟退火算法在每次迭代过程中，会进行一次降温操作，降低退火温度T。根据Metropolis接受准则，随着退火温度T的减小，劣质解的接受概率也随着降低，提升算法收敛速度。退火温度以及温度衰减系数的选择对于退火算法的收敛速度具有较大影响。

4. 仿真分析

为验证遗传模拟退火算法的性能，对遗传模拟退火算法进行了模拟仿真。仿真中假定光速 $c=3\times {10}^8$ 米/秒，雷达探测范围为1.5~180千米，距离分辨单元为150米，最大目标速度为1500米/秒，杂波宽度为500赫兹，多普勒分辨力为100赫兹，可选择重频范围为3.33~20千赫兹。交叉概率为0.6，变异概率为0.01，初始温度为1，温度衰减系数为0.7；初始样本数量为50，中止条件为迭代50次。

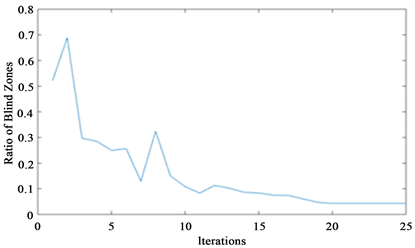
基于上述参数，运用遗传模拟退火算法对重频组合进行优化，对应的遮蔽率如图3所示。其中，图3(a)为利用遗传模拟退火算法对重频组合优化过程中，迭代过程中遮蔽率变化曲线图；图3(b)为迭代后的距离和多普勒遮蔽图，经计算优化后的距离和多普勒的遮蔽率为3.04%。

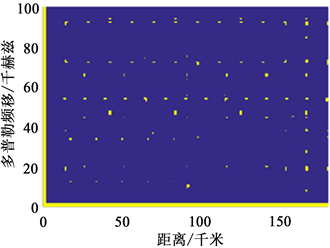(a) (b)

Figure 3. The optimization results of the range/Doppler blind zones. (a) The convergence curves of the blind zones in iteration; (b) the blind zones of range/Doppler after iteration

图3. 距离/多普勒遮蔽区域优化结果。(a) 迭代过程中遮蔽率变化曲线图；(b) 迭代后得到的距离/多普勒频移

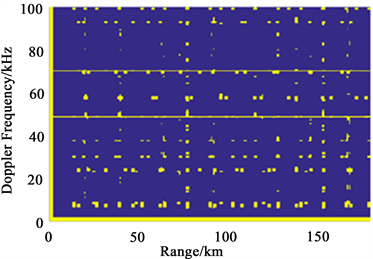
为更进一步探索遗传模拟退火算法的性能，作者编写了基于遗传算法和模拟退火算法的重频组合优化程序，利用相同的初始条件进行优化，结果如图4所示。其中，图4(a)为遗传算法的距离/多普勒遮蔽率优化结果，遮蔽率为5.14%，图4(b)为模拟退火算法距离/多普勒遮蔽率优化结果，遮蔽率为3.84%。因而，可得采用遗传模拟退火算法的进行重频组合优化选择的效果优于遗传算法和模拟退火算法。

(a) (b)

Figure 4. The optimized results of the range/Doppler blind zones using the two algorithms. (a) The optimized result using the genetic algorithom; (b) the optimized result using the simulated annealing algorithm

图4. 两种算法的距离/多普勒遮蔽率优化结果。(a) 遗传算法优化结果；(b) 模拟退火算法优化结果

5. 总结

本文提出了一种基于遗传模拟退火算法的重频选择方法，并对该方法的性能进行了试验验证。经验证，利用该算法对距离/多普勒遮蔽率进行优化，可降低遮蔽率至3.04%。而相同的初始条件下，遗传算法和模拟退火算法对距离/多普勒遮蔽率的优化结果分别为5.14%和3.84%。因此，利用该方法对中重频雷达的重频选择优化具备更好的收敛效果，能够获得更优的全局解。此外，考虑到算法的收敛速度和求解结果受初始退火温度和衰减系数的限制。后续研究中，可通过优化初始温度和衰减系数，实现算法性能的进一步提升。